平均の出し方を根本から理解する！ 合計・個数を求める公式や面積図を解説

中学受験算数では平均の問題がよく出ます。小学校の算数でも平均について学ぶので、ほとんどの受験生は「平均」という言葉や平均の出し方・求め方は知っています。一方で、「平均とは何か？」を理解できておらず、少し難しい問題になった途端、手も足も出なくなることも少なくありません。このような受験生のために、平均の出し方を根本から理解できるように解説します。

「平均とは何か？」を理解する

「平均」という言葉の意味を理解すれば、平均の公式の意味や面積図の使い方もわかります。

「平均」とは「平らに均すこと」

「平均」は「平らに均（なら）す」という意味です。具体的には、でこぼこをなくして、一つひとつを同じ大きさにすることを表します。

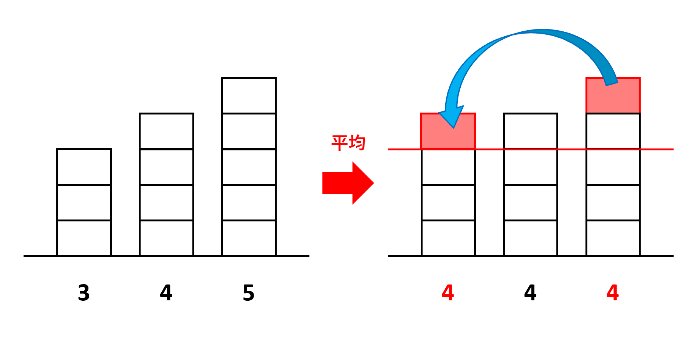
たとえば、3、4、5の平均を考えましょう。下の図では、でこぼこ状態（左）を平らに均しました（右）。5個の長方形の1個分が3個の上に移動して、すべて4個になったことがわかります。このように、でっぱった部分をへこんだ部分に移動するのが平均です。

「合計÷個数＝平均」の公式

平均には「合計÷個数＝平均」という公式があります。この公式が正しいことは、3、4、5の平均が（3＋4＋5）÷3＝12÷3＝4となることからも明らかでしょう。一人ひとりが持っているものをすべて回収して、それを平等に再分配するイメージです。

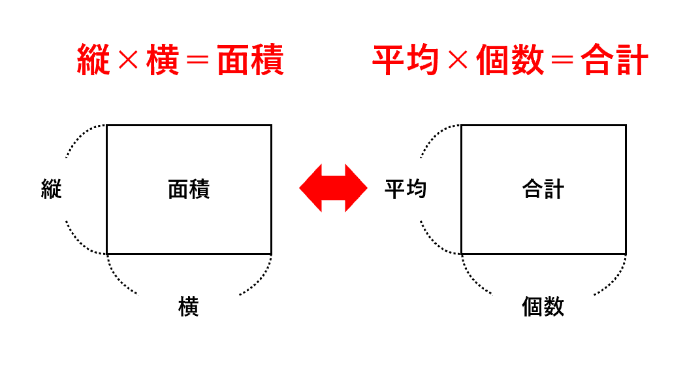
また、公式を変形すれば「平均×個数＝合計」「合計÷平均＝個数」になります。「平均×個数＝合計」は「縦×横＝面積」と形が似ています。そのため、縦を平均、横を個数とし、面積を合計とする面積図で表すこともできます。

中学受験算数にも使える！ 「面積図」と「インド式計算」で2桁の計算を工夫する

「インド式計算」、この言葉を聞いたことはあると思います。インドは数学の「0（ゼロ）」の概念の発祥地としても知られていま...

平均の出し方を利用した問題の解き方

平均の出し方を利用して、実際に問題を解いてみましょう。

公式を利用する平均の問題

Cの身長を□cmとします。公式にあてはめて□を求めましょう。

3人の身長の合計は、「平均×個数＝合計」より161×3＝483（cm）です。また、□を使って3人の身長の合計を表すと、165＋158＋□＝323＋□＝483が成り立ちます。逆算して□＝483－323＝160（cm）が答えです。

仮平均を利用する平均の問題