
何通りあるかを計算で求めよう! 「場合の数」が苦手な小学生のための公式の使い方
ある事柄が起こる場合を全て数え上げて、「何通りあるか?」を求めるのが「場合の数」です。全ての場合を書いて数えれば正解は出るはずですが、地道に数えていると抜け漏れが生じてしまうこともありますし、時間的に全ての場合を数え上げるのが難しい設問になっていることもあります。こうした設問に対応するためには、場合の数を計算で解く方法を知っておくといいでしょう。今回は、小学生でも理解できる「場合の数の計算方法」を紹介します。
順列の公式Pはどういう意味?
場合の数の問題は、並び順を考える「順列」と、並び順を考えない「組合せ」に大きく分かれます。まずは、次の問題を考えてみましょう。
1、2、3、4、5の書かれた5枚のカードから2枚を取り出して2桁の整数を作ります。全部で何通りの整数ができますか。
たとえば、「1」と「2」という2つのカードを並べたとき、12と21は別の整数になるので、並び順を考えなければならない「順列」の問題だとわかります。小学校の算数の授業では、順列の問題は樹形図(全ての場合を枝分かれで表した図)を描いて数え上げます。
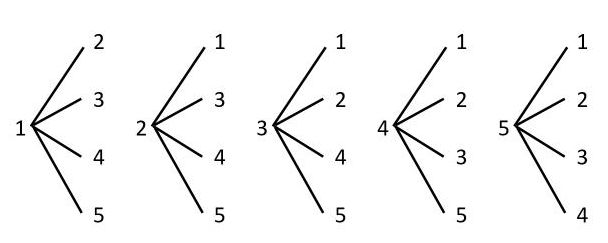
樹形図から答えは20通りです。一番左側の1で始まる図を描いて、「これと同じ図が5つできる」と気づけば、4×5=20(通り)と答えを求めることもできます。
では、樹形図を描かずに答えを求める方法はないのでしょうか? 高校数学では次の公式を学びます。
異なるn個のものからr個取り出して並べる順列は、nPr
Pは「パーミュテーション」といいます。難しそうな公式ですが、多くの中学受験生はこの公式と同じ方法で計算しているはずです。上の問題を次のように考えてみましょう。
十の位に来る可能性のある数は1~5の5通り。一の位に来る可能性のある数は、十の位で使った数を除いた4通り。積の法則より5×4=20(通り)。
ある事柄Aの起こり方がa通りで、それぞれの場合について、他の事柄Bの起こり方がb通りあるとすると、AもBも起こる場合の数はa×b通りになります。これを積の法則といいます。上の問題では、十の位の数字が1~5の5通りです。そして、たとえば十の位が1のとき、一の位は2~5の4通りです。このように十の位が1~5のそれぞれについて一の位が4通りあるので、5×4という積の法則が成り立ちます。この5×4が 5P2 (異なる5個のものから2個取り出して並べる順列の公式)の正体です。
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

