仕事算の問題を解くコツは？ 仕事量全体の数値を決めて1日の仕事量を求めよう

仕事算とは、複数の人たちで作業に取り組んだ場合の時間や日数を求める計算のことです。たとえば千羽鶴を折るときに1人で折ると10日間かかる場合、2人で折れば5日間、5人で折れば2日間で終わると予想できるでしょう。

このように、千羽鶴を折るなどの作業を「仕事」といい、何人いれば何日で仕事が終わるのかといった計算を行うのが仕事算です。この仕事算を苦手とする受験生は多いですが、実は難しくありません。今回は仕事算の基本問題から少し応用的な問題までを解説します。

基本問題で仕事算の解き方を確認しよう

まずは基本問題で仕事算の解き方を確認しましょう。

このタイプの問題の解き方はワンパターンです。ただし、最初の段階で仕事にどのような数値を設定するかで、解きやすさに差が出てきます。今回は2種類の解き方を紹介します。

仕事算の解き方1：仕事量全体を「1」にとする解き方

まず、仕事量全体を「1」にとして考えてみます。この場合、下の図のように、A、B、Cの1日の仕事量を求めると、それぞれ\(\frac{1}{9}\)、\(\frac{1}{8}\)、\(\frac{1}{6}\)だとわかります。

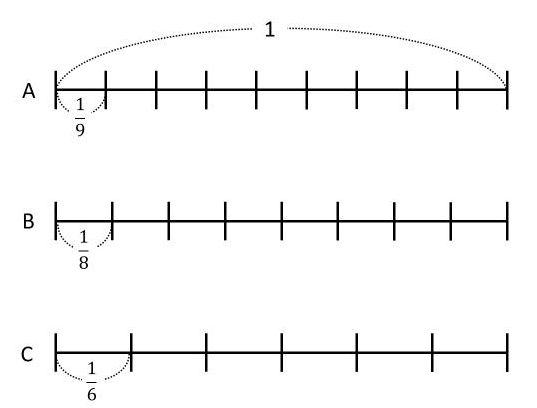
3人がいっしょにこの仕事をすると、1日の仕事量は\(\frac{1}{9}\)＋\(\frac{1}{8}\)＋\(\frac{1}{6}\)＝\(\frac{29}{72}\)になるので、かかる日数は1÷\(\frac{29}{72}\)＝2\(\frac{14}{29}\)（日）と求められます。したがって、この仕事は3日目に終わります。

仕事算の解き方2：最小公倍数を利用する

仕事量全体を「1」とすると、A、B、Cそれぞれの1日の仕事量が分数になって、計算が面倒です。そもそも仕事量全体はどんな数値をおいても構いません。このことをふまえて、仕事量全体を9でも8でも6でも割り切れる数、すなわち9と8と6の最小公倍数「72」として考えるのもありです。そうすると、下の図のように、A、B、Cの1日の仕事量がそれぞれ8、9、12となります。

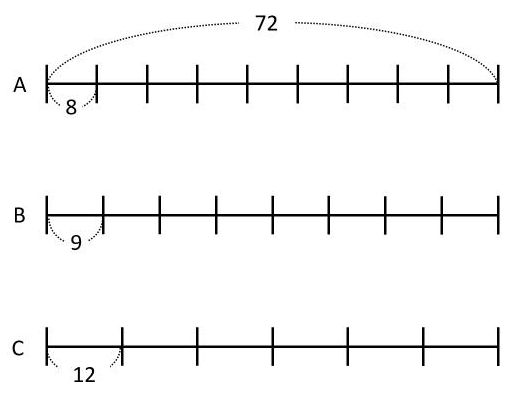
3人が一緒にこの仕事をすると、1日の仕事量は8＋9＋12＝29になるので、かかる日数は72÷29＝2\(\frac{14}{29}\)（日）です。仕事量全体を「1」とおいたときと全く同じ答えになります。

分数の計算でミスをしてしまいがちな受験生は、この最小公倍数を利用する解き方のほうがいいでしょう。ただし、この発想がどうしても思い浮かばないのなら、どんな場合でも仕事量全体を「1」としたほうが混乱せずにすみます。どちらでも同じ結果になるので、好きな解き方を選んでください。