等積変形で難しい面積問題をサクッと解決！ 平行線と三角形の関係がおもしろい

中学受験算数の平面図形分野では、面積を求める問題が頻出です。複雑な形の図形の面積を求める場合、図形をいくつかに分ける、全体から不要な部分を引くなど、さまざまな工夫があります。そのなかから、今回は「等積変形」を紹介します。

等積変形というと難しいイメージがあるかもしれませんが、使いこなせるようになると便利です。しっかり理解して、図形問題攻略の武器にしましょう。

等積変形を理解しよう

等積変形とは、図形の面積を変えずに形を変えることです。等積変形の方法にはいくつかの種類があります。しかし、中学受験算数で等積変形という場合、平行線と三角形の性質を利用した変形がほとんどです。

三角形の面積は「底辺×高さ÷2」で求められます。したがって、底辺と高さがそれぞれ等しければ、面積は等しくなります。

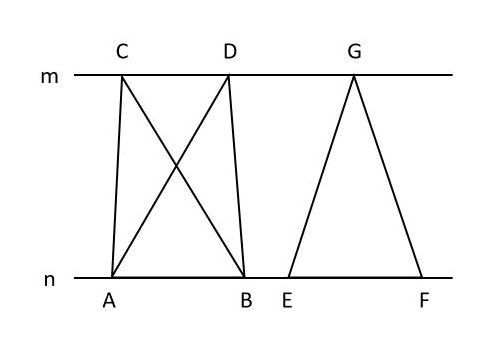
たとえば、上の図で直線mと直線mが平行ならば、底辺が共通の三角形ABCと三角形ABDは面積が等しいです。平行な2直線はその間の距離がどこでも同じなので、CからABに下した垂線とDからABに下した垂線の長さが等しくなり、三角形ABCと三角形ABDの高さも等しいからです。

また、三角形EFGについても、EFの長さとABの長さが等しければ、三角形EFGは三角形ABCや三角形ABDと面積が等しいといえます。

このように、平行線と三角形が与えられた求積問題では、多くの場合、等積変形を利用して面積を求めます。

等積変形の基本に慣れよう

実際に、等積変形を利用する求積問題を考えてみましょう。

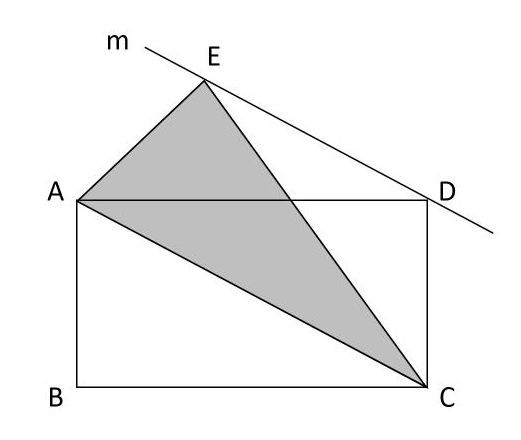
下の図より、三角形ACEと三角形ACD（長方形ABCDを二等分した三角形）は底辺ACが共通で、高さも等しいとわかります。