ベン図の活用で集合算が得意に！ 和集合や共通部分の関係を理解しよう

いくつかのものの集まりが「集合」です。集合は高校数学で本格的に学びますが、中学受験算数でも「集合算」という特殊算として出てきます。この集合算で役立つ「ベン図」について解説します。

ベン図の基本を理解する

ベン図を描いて問題を解く上で、大切な用語や考え方を解説します。

ベン図に関係する用語

集合が与えられた場合、その集合に含まれるものすべてをまとめて「全体集合」といいます。たとえば、「30人のクラスで、犬を飼っている児童が12人いる」という場合、全体集合は「クラスの全児童30人」です。

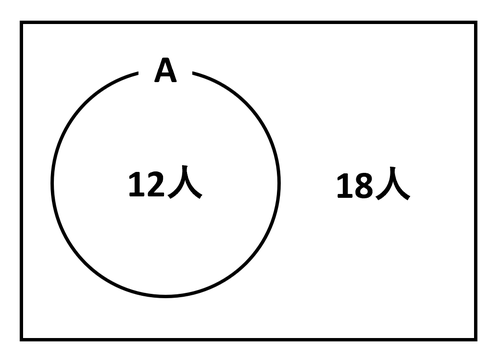
ここで「犬を飼っている児童12人」を集合Aとしましょう。Aに含まれていないものをまとめて「Aの補集合」といいます。Aが「犬を飼っている児童12人」ならば、Aの補集合は「犬を飼っていない児童18人」です。「全体集合－A＝Aの補集合」です。これをベン図で次のように表せます。

「30人のクラスで、犬を飼っている児童が12人いて、猫を飼っている児童が16人いる」という場合、「猫を飼っている児童16人」を集合Bとすると、「犬も猫も飼っている児童4人」はAとBの両方に含まれます。このように、AとBの両方に含まれるものをまとめて「AとBの共通部分」といいます。

また、AとBの少なくともどちらか一方に含まれるものをまとめて「AとBの和集合」といいます。ここまでの例だと、「犬か猫の少なくとも一方を飼っている14人」がAとBの和集合です。

和集合と共通部分の関係

AとBの集合の関係をベン図で表すと次の通りです。図の人数はそれぞれ「犬を飼っているが猫を飼っていない児童8人」「猫を飼っているが犬を飼っていない児童12人」「犬も猫も飼っている児童4人」「犬も猫も飼っていない児童6人」を表します。

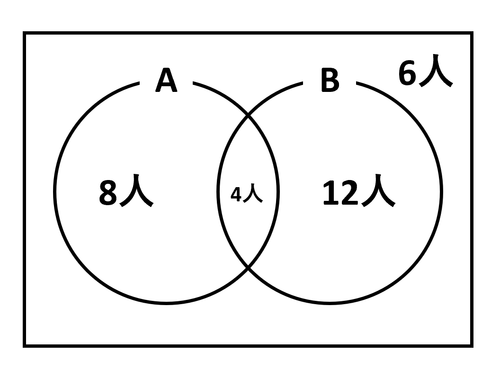
ベン図から、「A＋B－AとBの共通部分＝AとBの和集合」が成り立つことも明らかでしょう。

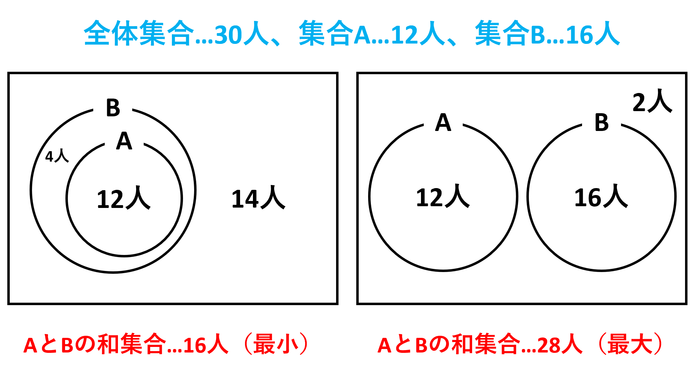
また、和集合と共通部分の関係で注意したいのは、次の2つです。

ベン図で問題を解く

ベン図を描きながら集合算を解いてみましょう。

典型的な集合算の問題

まずは集合算の基本問題です。