
算数の平面図形を苦手にさせない! 小学生のうちに身につけたい習慣とは?
中学受験の勉強の中でも「平面図形が苦手」という小学生は多いです。しかし、苦手意識を持っているのは子供だけではありません。平面図形の問題は大学の一般入試問題にも出題されます。大学入試センター試験でも選択問題で出題されますが、選択する学生は少数派です。このように、小学生の子供だけでなく、大学受験生でも苦手意識を持つ子が多いのが平面図形の問題なのです。
Contents [hide]
平面図形を苦手にさせない ――「図形を描く習慣」があるか
実は平面図形の得意・不得意には、小学生からの「ある習慣」の有無が影響しているといわれています。その習慣が「図形を描く習慣」です。
図形を描くことで育つ2つの力
平面図形の問題を解くとき、先生に「ノートに図を描くようにしなさい」といわれた経験がある人は多いでしょう。しかし、問題に図形が載っていると、「わざわざノートに写す意味がない」と思う子は少なくありません。「問題に載っている図に、直接書き込んで解けばいい」と思う子もいます。
ですが、ノートに図形を描くことは重要です。なぜなら、問題を解くうえで必要な次の2つの力が身につくからです。
■図形を描くことで育つ力
[1]情報を整理する力
[2]図形の成り立ちを理解する力
この2つの力を身につける重要性を詳しくみていきましょう。
情報を整理する力
文章題では情報が文字で記述してあります。文字は字面通りに読めば、ある程度見落とさず整理することができます。一方で平面図形の問題は、図形から情報を読み取らなくてはいけません。漫然と図形を眺めているだけでは、情報を見落としてしまいがちです。図の情報を整理するために、自分で図を描く作業は欠かせないのです。
図形の成り立ちを理解する力
情報の整理ができたら、その情報が「どのように関連しあっているか」を理解する必要があります。たとえば、角度を求める問題の場合、答えがひとつに定まる必然性があるはずです。正しい順番で図形を描けるようになると、答えに辿り着くためのポイントや順番も自然と見えてきます。
平面図形を苦手にさせない ――正しい図形の描き方
平面図形の問題で図形を描くときは、次の2点を意識することが大切です。
■図形を描くときに意識したいこと
[1]フリーハンドで描く
[2]線をなぞらずに描く
小学生とくに低学年の場合、いきなりこの2つを会得するのは難しいでしょう。ですから、最初は定規を使ってもよいです。ただし、定規を使って図形を描くのは、あくまでフリーハンドで描くための前段階です。運筆力を鍛えて、いずれはフリーハンドで描けるようにしたいものです。
小学校では「定規を使ってきれいに描きましょう」という指導があります。ですが、「定規できれいな図形を描くこと」が目的となって、フリーハンドで描く子に対し先生が「定規を使いなさい」と指導することがあるようです。
しかし、平面図形の問題で「定規できれいな図形を描くこと」は目的ではありませんよね。コピー機のように丁寧にノートに写す必要はないのです。情報を整理し、図形の成り立ちを理解し、問題の答えにすばやく辿り着くために図形を描きます。そのためには、「フリーハンドで描く」「線をなぞらずに描く」この2点を意識して図形を描くことが大切なのです。
平面図形を苦手にさせない ――フリーハンドでなぞらずに図形を描く
フリーハンドで描いた図形の例をみてみましょう。次の図1~3を見てください。
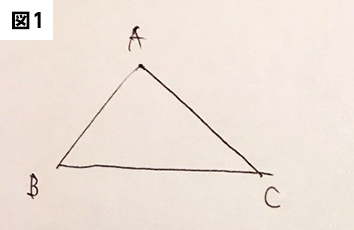
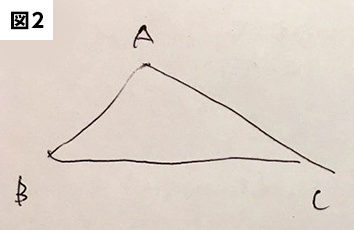
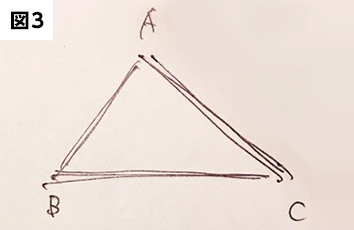
図1がフリーハンドで正しく描かれた三角形であるのに対して、図2はまだフリーハンドで直線を描くのに慣れていないのがわかります。
また図3のように直線をなぞって複線のように書いてしまう子もいます。絵画やデッサンを描くときに、こういった鉛筆の使い方をすることがあるようですが、平面図形の問題を解くには、望ましくない図形の描き方です。図3のように、線をなぞって描くクセがある子には、しっかりと注意してあげるとよいでしょう。
平面図形を苦手にさせない ――例題で図形を描いてみる
では「図形を描く力」をどのように生かしていくのか、例題で紹介します。
■[例題1]角Aの大きさを求めなさい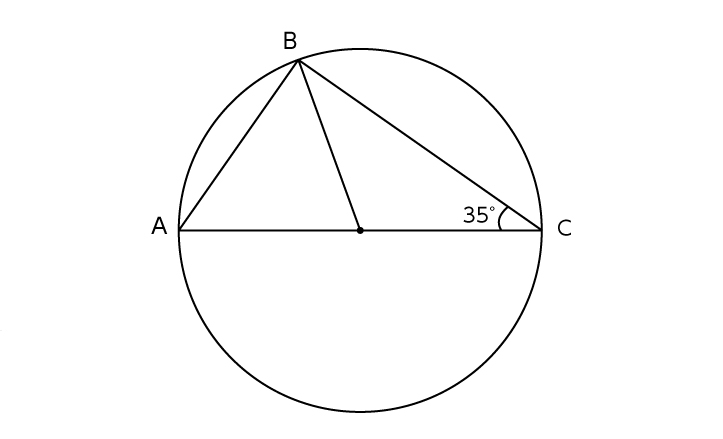
この問題はとてもシンプルな問題です。線分ABが「直径である」ことを見抜けないと解けないのがポイントですね。問題と同じ図を自分で、フリーハンドで描いてみます。
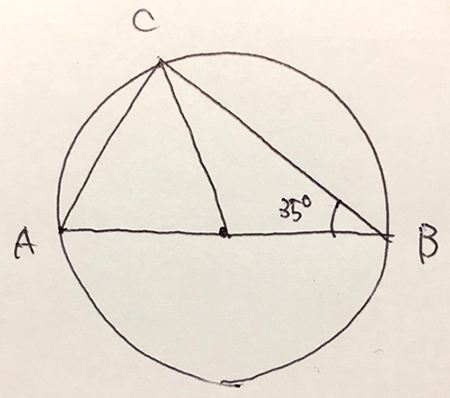
このように、図を描くには円を描いたあと、線分ABを描かなくてはいけません。となると、このときに「線分ABはどこに描けばよいのだろう?」という思考が生まれます。
前述したような、「コピー機のように写す」という作業の場合、きれいに描き写すことに意識が集中してしまい、線分ABが直径になっているのを見落としがちです。
自分で図を描くことで、答えにたどり着くためのポイントや、順番がみえてくるわけです。
では、もう一問例題で解説しましょう。
■[例題2]ア、イの角度の大きさを求めなさい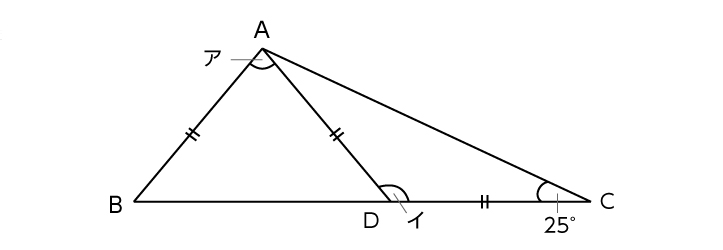
ちょっと意地悪な出題ですね。というのはア→イではなく、イ→アの順番で求めないといけない問題だからです。この問題も図形を描く習慣があると解きやすくなります。同じ図を自分で、フリーハンドで描いてみましょう。
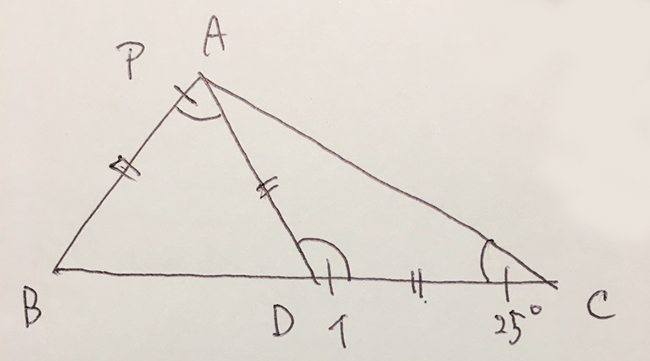
△ACDは2辺の長さが等しいことと、1つの角度がわかっています。二等辺三角形なので、それぞれの角度を出すことができ、三角形の形が決まるので、図形を描くことができます。
一方で△ABDは2辺の長さが等しい二等辺三角形ということ以外、ほかに情報がなく、形が決まっていません。
ですから、△ABDの三角形から描こうとすると、出題された図をみて何となく形を「写す」しかないわけですね。
しかし、△ACDのほうは順を追って角度を求めていけば、形が決まるので「描ける」とわかるはずです。「△ACDのほうから描けばいいんだ」となれば、答えに辿り着く順番(イ→アで角度を求める)も見えてきやすいのです。
このように、図形を描く習慣が身についていると、問題の図を見たときに「イ→アの順で解くべきだ」と見抜く力がつきます。
平面図形を苦手にさせない ――長期的な視点で、まずは「図形を描く習慣」を
言い古された基本ではありますが、平面図形の基礎を鍛えるには「図形を描く習慣」が欠かせません。この習慣は、中学受験はもちろん、その後の学習にも大きく影響します。目先の問題を早く解くばかりではなく、ときには腰を据えてじっくりと、図形を描く習慣を身につけていきたいものです。
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

