円錐の表面積を公式で求めよう！ 母線と底面の半径だけで簡単に計算できる

円錐の表面積を求める場合、底面の円の面積と側面の扇形の面積をそれぞれ求めて足すのが一般的です。しかし、扇形の面積を求めるときに割合の考え方が必要となるため、手が止まってしまう受験生も少なくないでしょう。

一方、「表面積＝（半径＋母線）×半径×3.14」「側面積＝母線×半径×3.14」という公式を使うと、割合を一切意識せずに表面積や側面積を求められます。これらの公式が成り立つ理由を理解した上で、実際に使ってみましょう。

公式が成り立つ理由を考えてみよう

最初に公式に頼らず円錐の表面積を求める方法を確認しましょう。

側面の扇形の面積を求めよう

母線が12cm、底面の半径が4cmの円錐の表面積を求めます。まずは、側面積から求めたいと思います。とりあえず見取図と展開図を描きました。

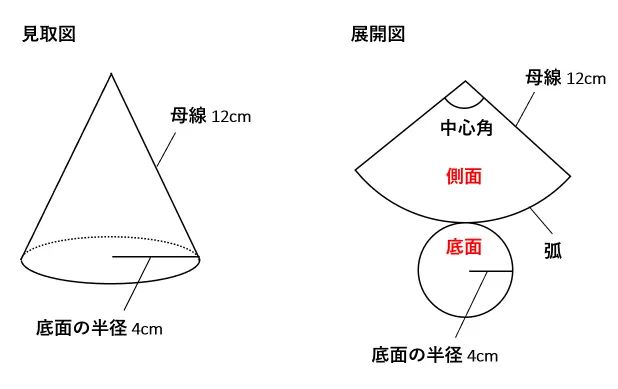
底面積は4×4×3.14で簡単に求められます。一方、側面積は、扇形の中心角の大きさがわからないので、すぐに求められないかもしれません。

そこで、扇形がどのような図形なのかを復習します。

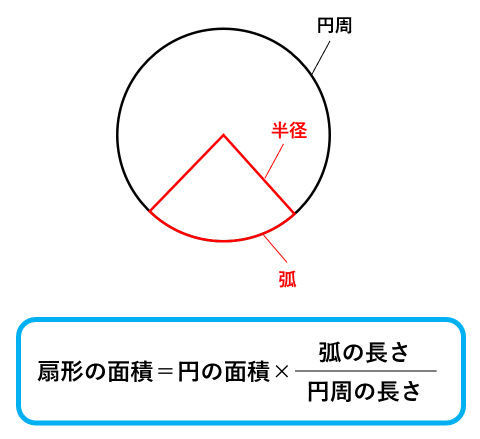
上の図からもわかる通り、扇形は円の一部です。

したがって、扇形の面積は、もとになる円の面積に割合をかけて求められます。

このときの割合は「\(\frac{弧の長さ}{円周の長さ}\)」です。

母線が12cm、底面の半径が4cmの円錐の側面積を求めましょう。

扇形の半径に当たるのは母線なので、円の面積＝12×12×3.14です。円周の長さは12×2×3.14、弧の長さは底面の円周の長さに等しいので4×2×3.14です。

したがって、側面積＝12×12×3.14×\(\frac{4×2×3.14}{12×2×3.14}\) で、2×3.14を約分すると側面積＝12×12×3.14×\(\frac{4}{12}\)で求められます。

表面積＝底面積＋側面積＝4×4×3.14＋12×12×3.14×\(\frac{4}{12}\)＝（16＋48）×3.14＝200.96（cm\(^2\)）が答です。

表面積の公式を導いてみよう

底面積＝4×4×3.14は「底面積＝半径×半径×3.14」です。

また、側面積＝12×12×3.14×\(\frac{4}{12}\)は「側面積＝母線×母線×3.14×\(\frac{半径}{母線}\)」なので、「母線」を約分すると「側面積＝母線×半径×3.14」です。

したがって、「表面積＝底面積＋側面積＝半径×半径×3.14＋母線×半径×3.14」となり、「半径×3.14」を（　）の外に出して「表面積＝（半径＋母線）×半径×3.14」の公式が成り立つことがわかりました。