2進法を小学生にもわかりやすく解説！ 10進法で表された数も簡単に変換できる

私たちは普段、0～9の10個で表せる数を使っています。このような数の表し方を「10進法」といいます。一方、0と1だけで数を表すのが「2進法」です。

中学受験算数では、問題を解くうえで2進法を知っていると便利なことがあります。今回は10進法と2進法の関係に迫りつつ、2進法の考え方を使う問題を解説します。

2進法と10進法の関係を理解しよう

「10進法→2進法」と「2進法→10進法」のそれぞれの変換について理解しましょう。

10進法の数を2進法で表してみよう

10進法の2345＝2×1000＋3×100＋4×10＋5×1です。4桁の数は「（千の位）×1000＋（百の位）×100＋（十の位）×10＋（一の位）×1」と表せます。このように、10進法の数は、各位の数に1、10、100、1000、…をかけて足した数であることがわかります。

同じく2進法の数も各位の数に1、10、100、1000、…をかけて足していきます。しかし、2進法の1、10、100、1000、…は10進法の1、2、4、8、…です。したがって、10進法の19＝1×16＋0×8＋0×4＋1×2＋1×1は、×16、×8、×4、×2、×1を×10000、×1000、×100、×10、×1に書きかえることで、2進法の10011となります。

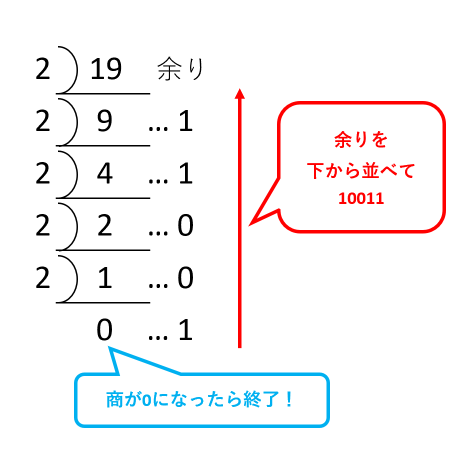
「10進法→2進法」に変換したい場合、商を2で割っていくのが簡単です。

2進法の数を10進法で表してみよう

2進法の数を10進法で表すには、ここまでで紹介したのと逆の操作を行います。2進法の1101＝1×1000＋1×100＋0×10＋1×1は、×1000、×100、×10、×1を×8、×4、×2、×1に書きかえることで、10進法の13（＝1×8＋1×4＋0×2＋1×1）となります。