二等辺三角形の面積をどうやって求めるの？ 考え方のコツは三角定規に着目すること

中学受験算数の平面図形分野では、二等辺三角形の面積を求める問題が出題されます。一見すると難しそうな問題ですが、考え方にはコツがあるので、それをわかっていれば簡単です。今回は、このコツについて詳しく解説します。

直角二等辺三角形に着目しよう

小学生は、中学数学で学ぶ三平方の定理を知りません。そのため、これから紹介する2種類の三角形に着目して、二等辺三角形の面積を求めることになります。

2種類の三角形のうち1つめは、直角二等辺三角形です。直角二等辺三角形は、2つの角度の大きさが45度になります。

また、正方形を四等分してできる三角形でもあります。

次の直角二等辺三角形の面積をそれぞれ求めましょう。

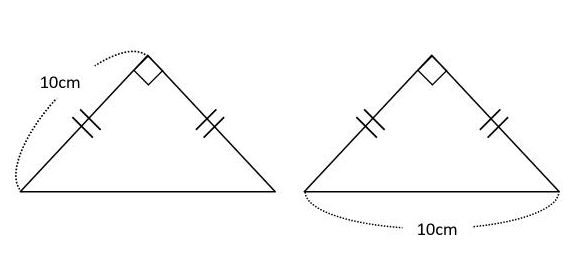
左側の直角二等辺三角形は、長さが10cmの二辺が底辺と高さになります。したがって、「面積＝底辺×高さ÷2」の公式を使って、面積は10×10÷2＝50（cm²）です。

一方、右側の直角二等辺三角形は一辺の長さしかわかりません。

しかし、ここで諦めてはいけません。10cmの辺を底辺としたとき、高さとなる補助線を図に書き込めばいいからです。

実際に補助線を書き込むと、もとの直角三角形が二等分されて、新しくできた三角形も直角二等辺三角形だとわかります。

これで高さの5cmを求められたので、面積公式に当てはめて10×5÷2＝25（cm²）です。

正三角形を二等分した三角形に着目しよう

直角二等辺三角形は、2つセットの三角定規のうちの1つです。そして、もう1つの三角定規もまた、直角三角形の面積を求めるのに大活躍します。ところで、そのもう1つの三角定規がどんな三角形か説明できますか？