天秤で考える算数｜桜井信一コラム「下剋上受験」

昔々あるところに、こんなのを間違える少女がいました。

ある日、少女が算数を解いていると、

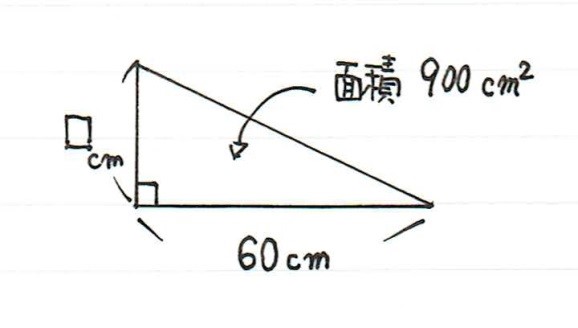
こんなことをし始めたのです。

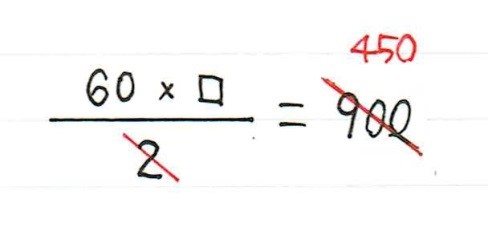
一見、何も問題なさそうに見えるこの式。

どうして答えが合わないのだろうと悩んでいると、

こんな約分はしてはいけないことに気付いたのです。

それは、少女が小学校5年生の秋のことでした。

レベル低っ！ って話なのですが、何度見ても答えが75cmになるのです。

しかし、答えはなぜか30cm。

図も30cmならちょうど良さそう。

とても不思議 (?_?)

これ、当然ミスでは済まされない。とんでもない勘違いをしているわけです。

算数の式を眺めるときに、あたまの中で天秤がゆらゆら動いていない証拠。単に計算しているだけで、つりあいを保とうという感覚がないわけです。

算数の式の「＝（イコール）」は当然つりあっている状態を表しています。

そのままどちらにも傾かないように、両辺に足したり、引いたり、かけたり、わったりしなければならないのです。

当たり前の話なのに、なんとこのときまで「＝（イコール）」の意味をはっきりわかっていなかったのです。

正しい式は言うまでもなくこちら。

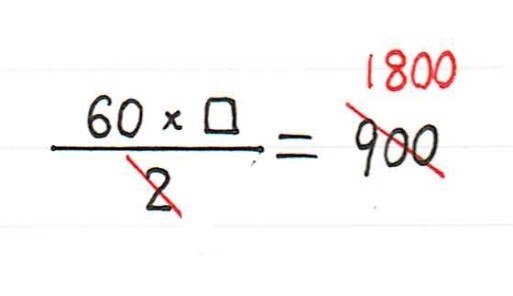
つまり、分母を消すという意味がよくわかっていなかったのです。

「あっ、そうなの？ わかった！これから約分はイコールの向こう側までしないようにするね」というのです。

そういう話？？？

そこで、こんな図を書いて見せました。

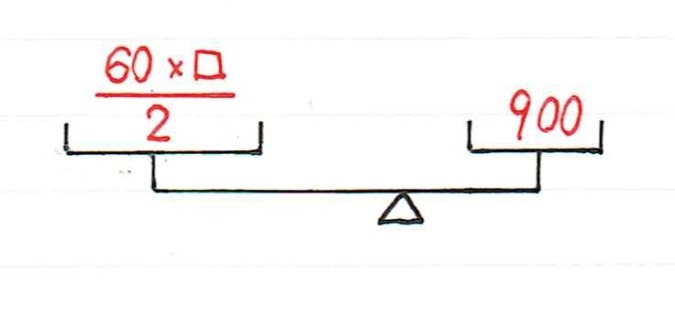
すると、ようやく理解できたようです。

小学校1年からずっと、「＝（イコール）」は答えを表すマークだと思っていたと言うのです。

合っているような間違っているような？？？

その後、猛勉強をしていくと小6の後半になって気付き始めました。

等式って、天秤と同じ話だったのだと。

そういえば、そんな話は私も習った記憶がない。
どうして図を書いて説明できるんだろう……。

なるほどっ！ きっと私の前世は数学者なのかもしれない。

ん？ ほんとか？

ちなみに先代は方程式も無理だぞ (?_?)

いや、何を気付いたかというと、この感覚が非常に重要なことに気付いたのです。

算数の文章題を解く上で、「つりあいを保つ」という感覚があれば、かなり広範囲の問題が解けるようになります。

そして、計算ミスが起きなくなってくるのです。バランスが崩れることを嫌う考え方になってくるわけです。数にボリュームを感じることができるようになってくるのです。

これは、中学進学後に習う方程式で強い味方になってくれる。

負の数や根号が登場するためにちょっとボリュームを感じにくくなっても、やはりつりあいを保つ作業に徹しようとするようになるのです。

結婚相手はつりあってないことを願っているけど (#^^#)

さらに、分母を消す作業を天秤の上で考える癖がつくと、中学になって片方だけルートをかけるような失敗がなくなります。有理化っていう名前になるのでちょっと本格的な気分になれてカッコいい。

ブログでも「せっかく勉強したものが本番で出なかった！」と嘆いていますが、中学受験の勉強って後々役に立つ場面が多いことに気付き、今は得した気分になっています。

そんな得したケースを今後もいくつかご紹介したいと思います。

では、興味がある人だけ天秤で考える問題を1つ練習して、本日のブログを終えたいと思います♪

問題を読んだ瞬間にどう思いましたか？

算数は感覚が大事だと思います。

それがないと、計算して出てきた答えに確信が持てないのです。

今回の場合、2：1 の状態から450円の本を買っただけで、5：1 まで大きくバランスが崩れてしまうのですから、もとの所持金に対してかなり大きな買い物だった気がします。

例えば、A君が2万円、B君が1万円持っていたとすると、450円の本を買ったくらいでは、そんなに大きく比は変わらないのです。つまりB君は 本を買ったあとあまりお小遣いが残っていなかった可能性が高いわけです。

まず、少ない方のB君のもとの所持金を（□円）とします。

するとA君は（□□円）ですね。

これで問題文の最初の 2：1 の状態になりました。

次に本を買う場面に進みます。

A君は　・・・　（□□円）－450円
B君は　・・・　（□円）－450円

このときのA君とB君の所持金の比が 5：1 なので、

ここから天秤がつりあうように式をつくると、右側を5倍にしなければつりあいません。

すると、こんな感じになります。「＝（イコール）」が天秤の支点だと思って重さを感じてください。

（□□）－450 ＝ （□□□□□）－450－450－450－450－450

両辺に分銅がのっているような感じになります。

これを整理すると、

（□□）－450 ＝ （□□□□□）－2250

いま、この状態で天秤はつりあっています。

この天秤に同じ重さを両方にのせてもやっぱりつりあうので、
2250円を両方にプレゼントします。

すると…

（□□）＋1800 ＝ （□□□□□）

もちろんまだつりあっています。

この状態から同じ重さを取り除いてもつりあったままなので、□を2個ずつ天秤からおろします。

すると…

1800 ＝ （□□□）

ということで、□1個が600円とわかります。

だからA君は1200円を持っていたことになります♪

最後までつりあった気分を保てたでしょーーーか。

（感覚を掴めたら、□×5　という書き方に変えていきましょう）

2014.10.7 am 0:00

桜井信一

※記事の内容は執筆時点のものです