食塩水の問題は素早く確実に解こう！ てんびん図を使った「早技」を紹介

食塩水の問題を苦手に感じてしまう子は少なくありません。「割合」の要素も含んでいるため、たしかに理解しづらい分野です。一方で、中学受験の算数の対策としてはぜひ押さえておきたい単元でもあります。中学入試本番でも頻出の、食塩水の問題。この単元をどうしても苦手に感じてしまう子に向け、簡単な方法で素早く、かつ確実に解く“技”を伝授します。

食塩水の問題の一般的な解き方

まずは次の問題を使って、食塩水の問題の一般的な解き方を見ていきましょう。

食塩水の問題を解くときは、「食塩の重さ」に注目するのが基本です。

上記の例題ですと、5%の食塩水に入っている食塩の重さは10g（200g×0.05）、10%の食塩水に入っている食塩の重さは30g（300g×0.1）なので、合わせると40g（10g+30g）となります。

そしてこの40gが500g（200g+300g）の食塩水のなかに入っていることになるので、答えは「8%（40g÷500g×100）」と計算できます。

てんびん図を使ってみよう

食塩水の問題の一般的な解き方をお伝えしましたが、より早く、そして確実に解くために「てんびん図」を使って解く方法も紹介します。

てんびん図とは

てんびん図とは、理科で学習する「てこのつり合い」で出てくる図のことです。

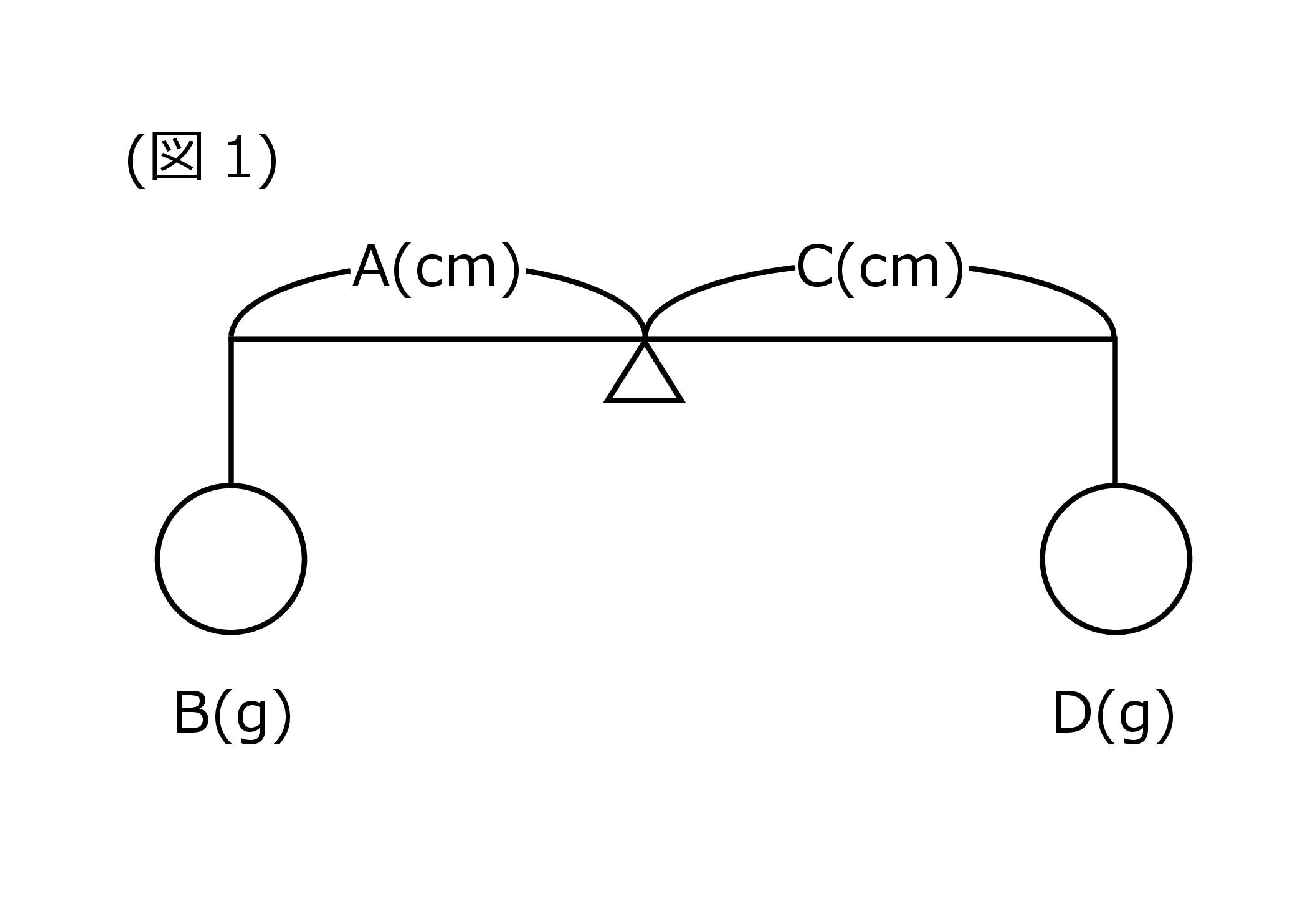
たとえば下の図1でいうと、A(cm)×B(g)=C(cm)×D(g)となれば、このてんびんはつり合っていることになります。

「比の性質」で考えてみよう

では次に、てこのつり合いを「比の性質」という点で考えてみましょう。

まず、○:□=◎:△という式があるとします。このとき、

が成り立つので、○×△=□×◎という式ができますね。

これと、先ほど見た「てこのつり合い」の式（A×B=C×D）を照らし合わせてみると、次のようにいえます。

ここから、てこのつり合いに関しては、次のそれぞれの比が逆の関係（逆比）になっていることが分かるでしょう。

今は比の性質をイメージできなくても、このあと紹介する例題のなかで図を使って見ていきますので安心してください。

てんびん図を使った解法

それでは、てんびん図を使って食塩水の問題を解く方法を紹介します。次の3つのパターンの問題について、一緒に考えていきましょう。

【1】食塩水を混ぜ合わせる問題

冒頭で紹介した例題を、今度はてんびん図を使って解いていきます。

まず、てんびん図を使うときのルールは次のふたつです。

実際に数値を当てはめると、下の図2のようになります。

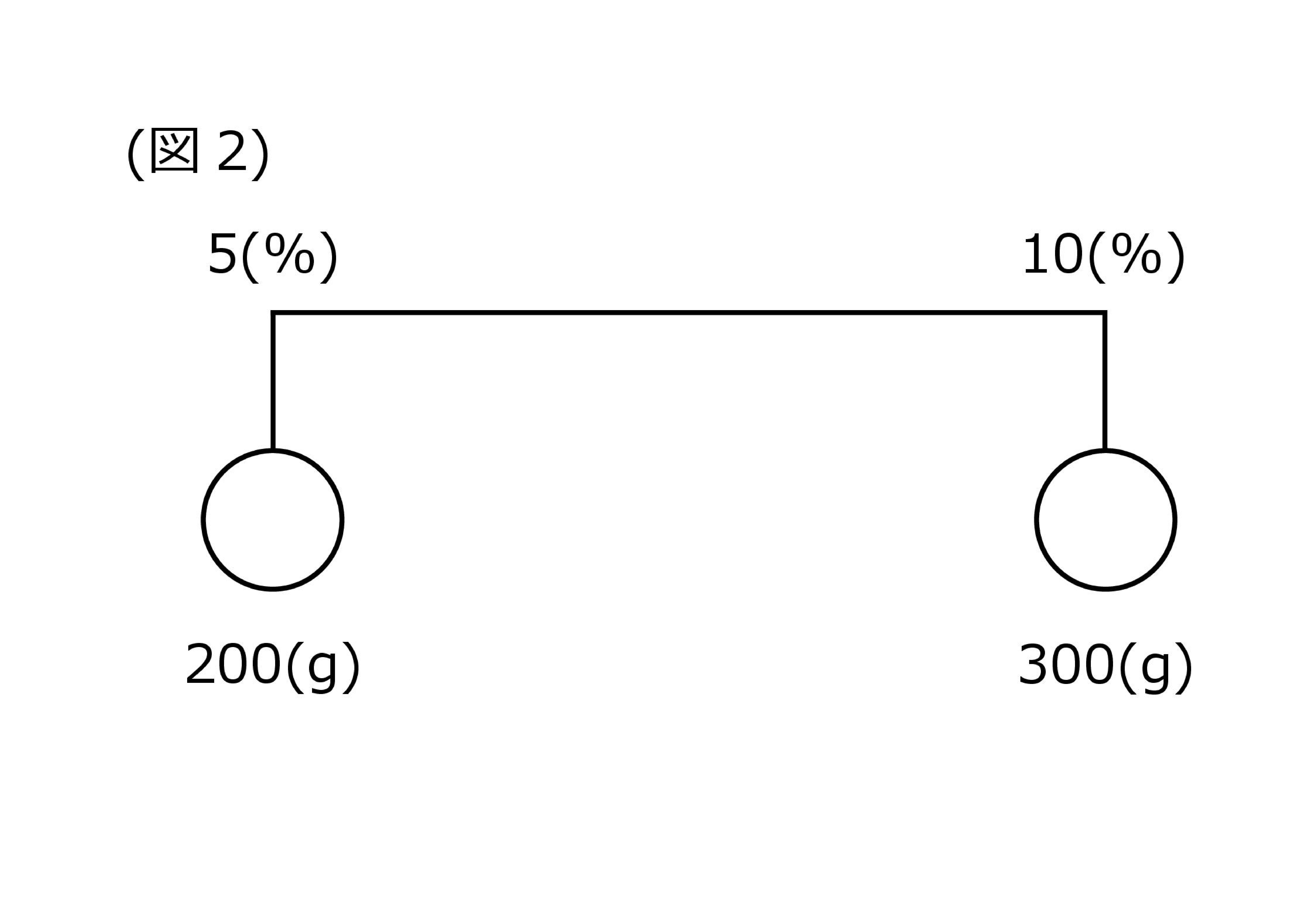
次に、おもりの重いほうに支点（△）を置きます。この支点の位置が「混ぜたあとの濃度」を指します。

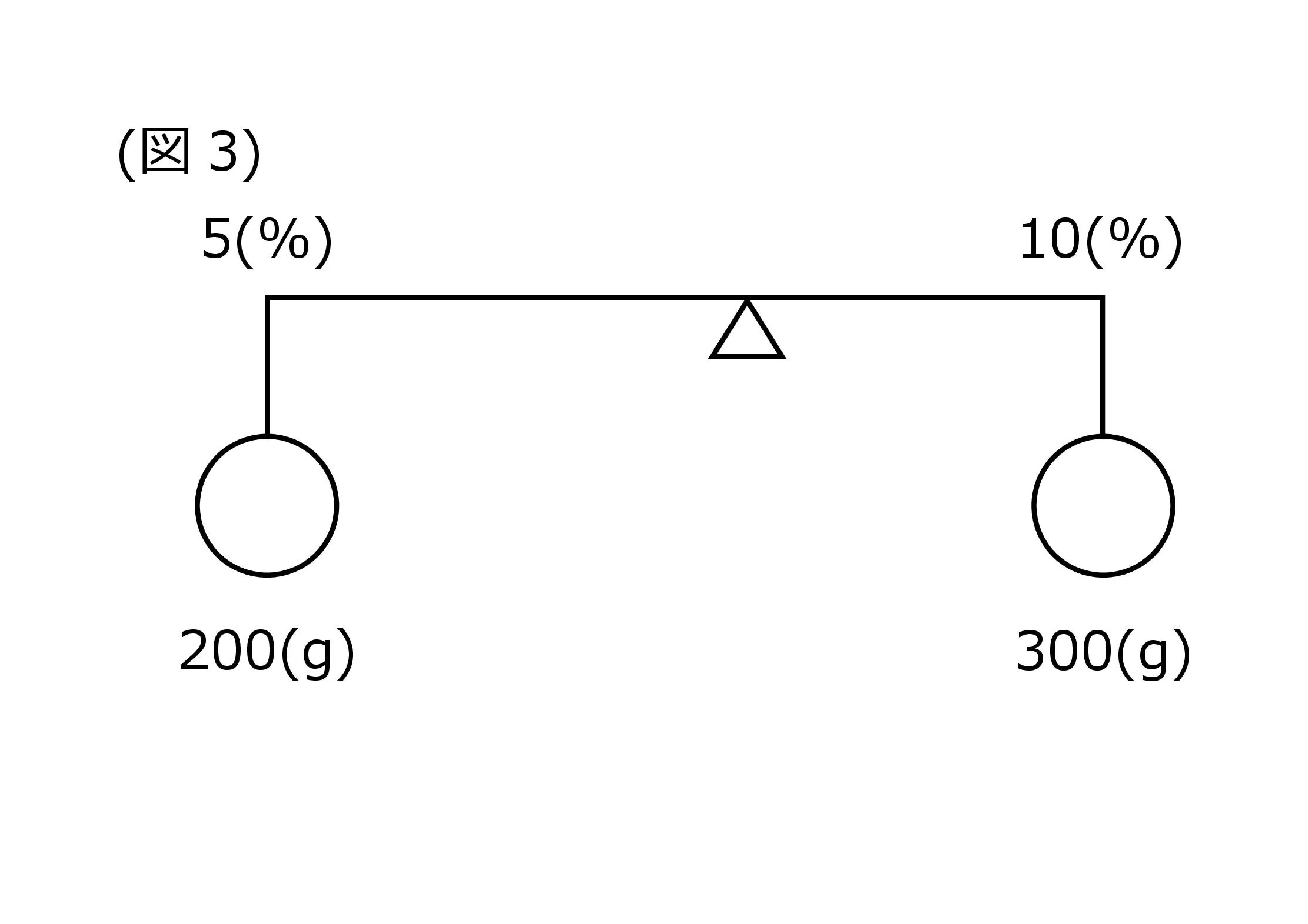
そしておもりの重さの比は2:3なので、支点からおもりまでの長さの比は逆の3:2になります。

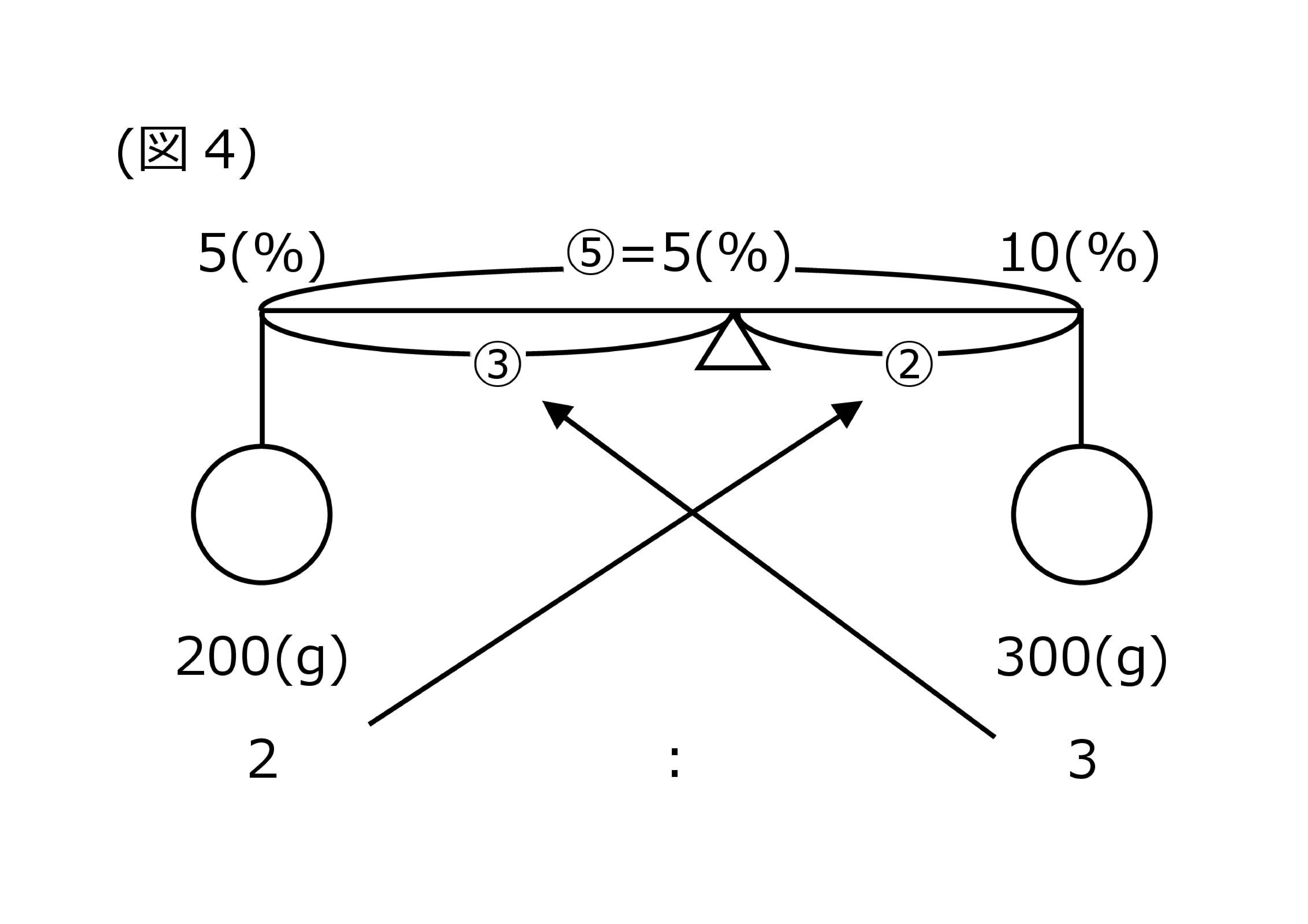
最後に、5%から10%までの長さを3:2で比例配分しましょう。まずは③の長さを求めると「3%（5÷5×3）」となりますね。そして左端の5%から3%ぶん濃度が高いところ、つまり混ぜた後の濃度は「8％（5％+3％）」ということがわかります。

【2】水や食塩を加える問題

次に、水や食塩を加える問題を考えてみましょう。

水を加える問題

説明は少し省きますが、先ほどの「食塩水を混ぜ合わせる問題」と同じステップで考えていくと下の図ができあがります。

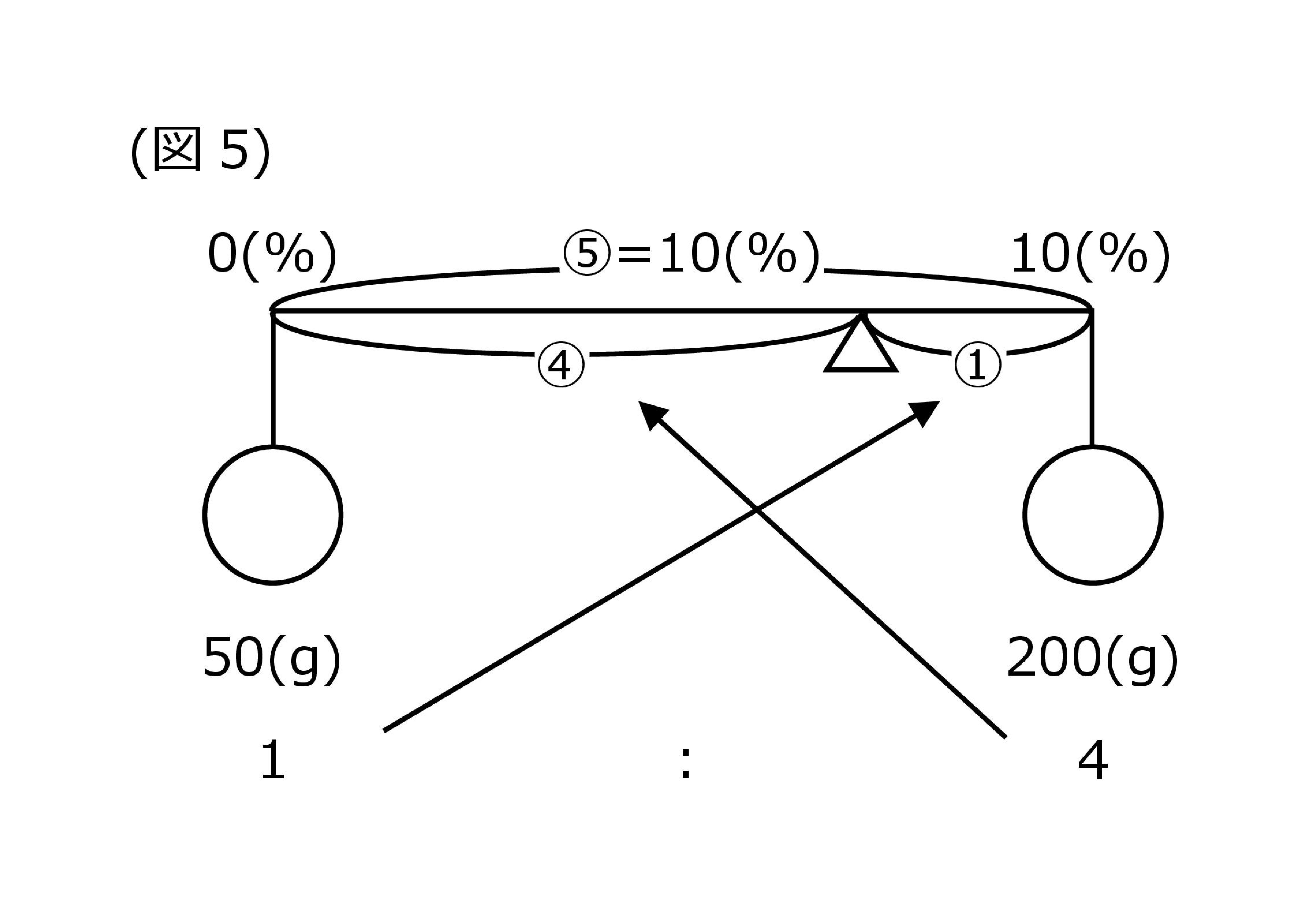
求める濃度は④の部分です。図をもとに計算すると、食塩水の濃度は「8%（10％÷5×4）」と導き出されます。

食塩を加える問題

食塩を加える問題の場合も、同じように解いていきます。

まずは、次の図を完成させましょう。

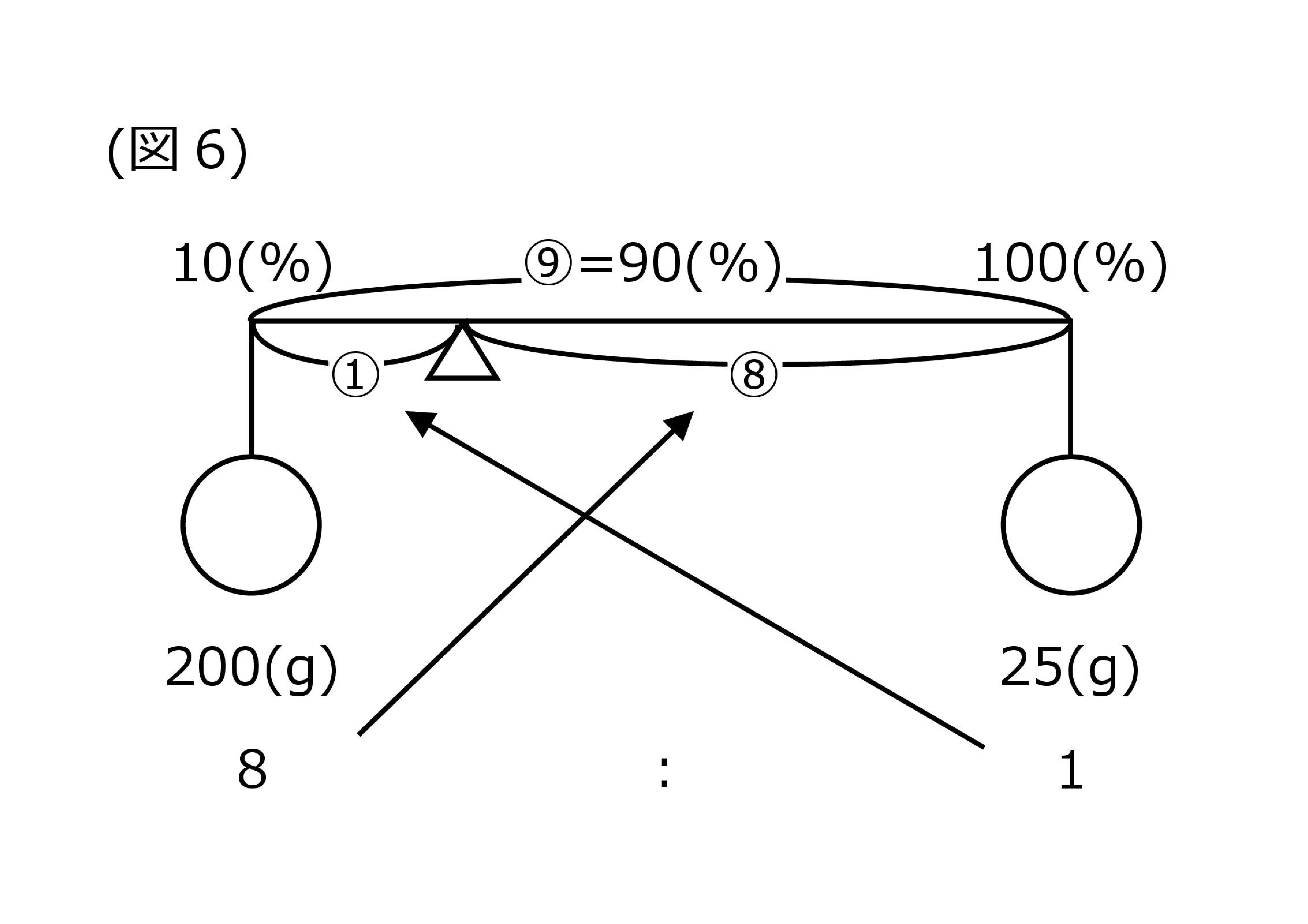
次に、①の長さを求めます。棒の長さが1:8に比例配分されているので、①の長さは「10%（90％÷9×1）」ということがわかりますね。つまり10%の食塩水200gに食塩を25g加えてできる食塩水の濃度は「20%（10％+10％）」ということです。

【3】水を蒸発させる問題

ここまで見てきた「混ぜ合わせる問題」では、混ぜたい食塩水をてんびんの両端に置いていました。では水を蒸発させた場合には、どのような図を書けば良いのでしょうか。次の例題をもとに、水を蒸発させる問題でてんびん図を使う方法を見ていきます。

水を蒸発させる場合には、支点の位置を少し変えるのがポイントです。具体的には右下に支点（△）を置きます。

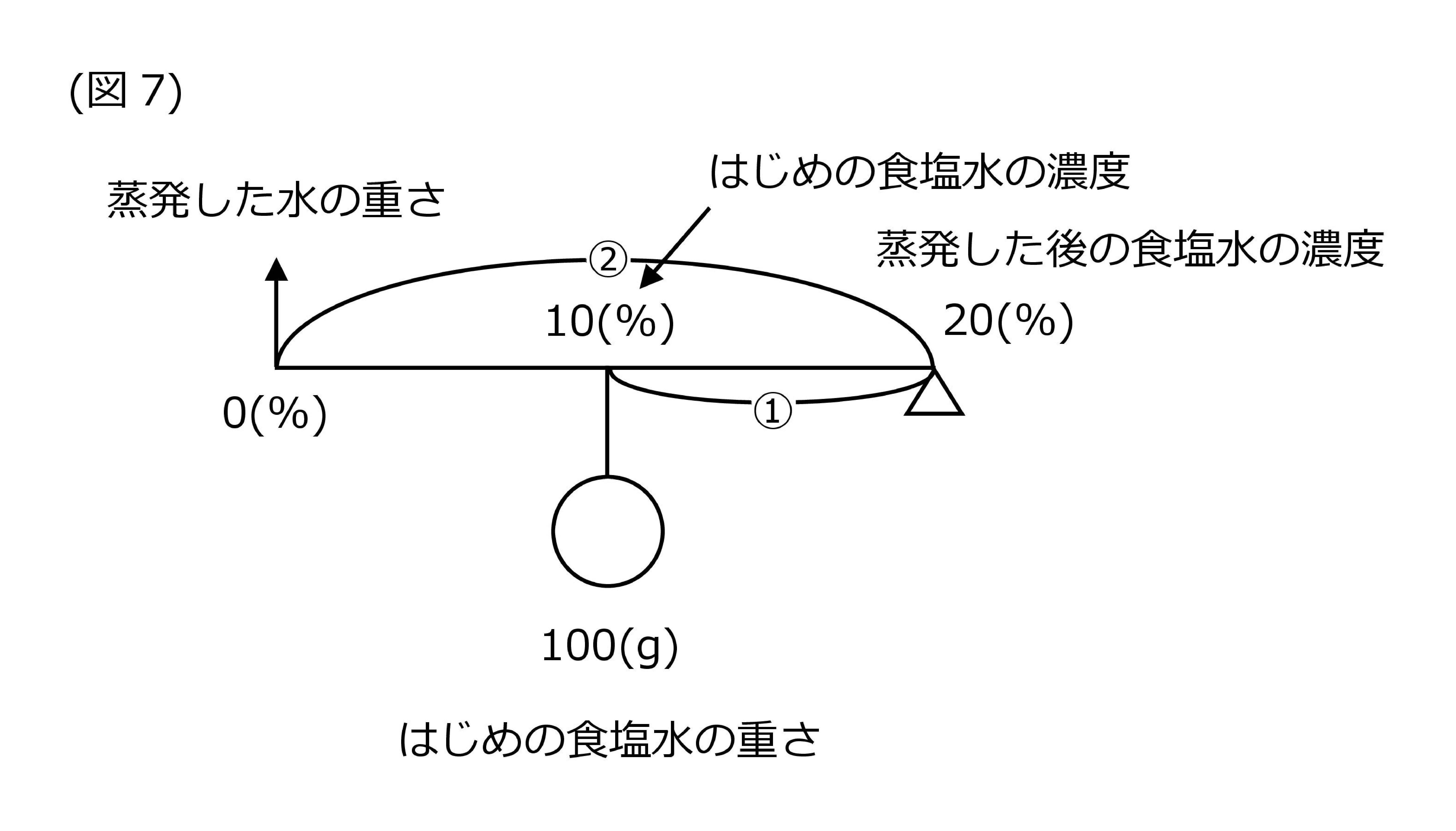
これまで見てきた図とは少し形が違いますが、支点からおもりまでの長さ、そしておもりの重さの関係が逆比となることは変わりません。

そのため次のような計算のもと、答えを「100g」と求めることができます。

てんびん図は「平均算」にも使える

てんびん図は食塩水の問題だけでなく、実は「平均算」の問題でも使えます。平均算の場合には、支点からおもりまでの長さに平均値を、おもりの重さに個数（人数など）を当てはめます。

では、例題を見てみましょう。

まずは食塩水の問題と同じく、次のようなてんびん図を書きましょう。

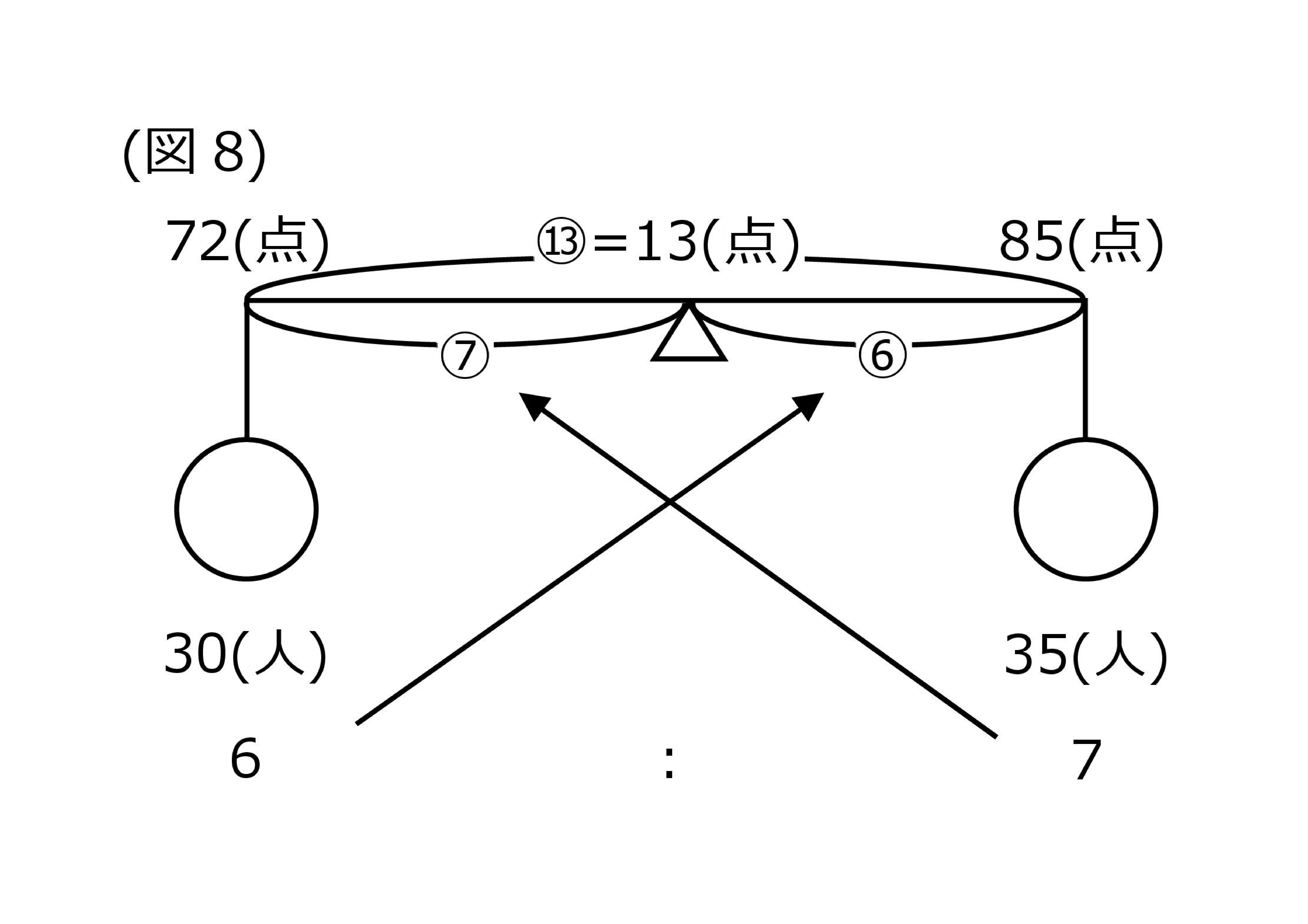
すると、13点を7:6に比例配分したときの⑦を先に求める必要があることがわかりますね。⑦を計算すると7点（13÷13×7）となるので、答えは「79点（72点+7点）」です。

まとめ

食塩水の問題は複雑な計算手順などがあり、中学受験生が苦手とする分野の筆頭です。しかし入試頻出単元でもあるため、対策は欠かせません。食塩水の問題に苦手意識を持っている子は、まずは今回紹介した「てんびん図」を使った解法をマスターしましょう。てんびん図の使い方をきちんと理解すれば、食塩水を混ぜ合わせる問題などを簡単に、かつ確実に解くことができます。食塩水の問題を得意にし、さらには得点源とすることで、ほかの受験生に差をつけていきましょう。

※記事の内容は執筆時点のものです