
中学受験算数にも使える! 「面積図」と「インド式計算」で2桁の計算を工夫する
「インド式計算」、この言葉を聞いたことはあると思います。インドは数学の「0(ゼロ)」の概念の発祥地としても知られていますね。そんなインドで使われているインド式の計算方法を、中学受験算数で学ぶ「面積図」をまじえて、一緒に紹介します。
Contents [hide]
中学受験算数で学ぶ「面積図」
インド式計算の話をする前に、まずは「面積図」についてです。面積図とは、「A×B=C」のような式を「縦×横=長方形の面積」にあてはめて考えていく方法です。中学受験をする場合、多くの生徒が学習する解き方ですね。面積図を使うと、計算を目に見えるかたちに表せるのがメリットです。
たとえば、100×7だと、次のように面積図を描きます。
■[例]100×7
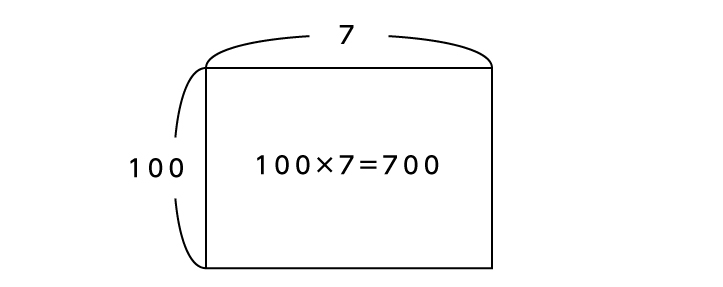
※画像は「面積図」を使った解き方のイメージです
※縦横の比率は、実際のものと異なります
「速さ」「平均」「濃度」といった問題も、この「面積図」を使って整理することができます。
「速さ」の問題で面積図を使う
■[例]毎分30mの速さで、120mの道のりを走ったときにかかる時間
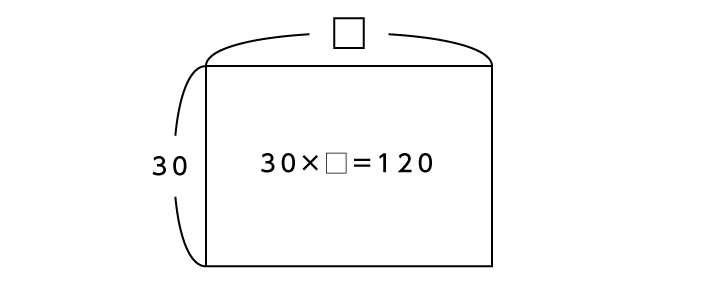
※画像は「面積図」を使った解き方のイメージです
※縦横の比率は、実際のものと異なります
速さ×時間=道のり
と考えると、
道のり÷速さ=時間
なので、
120÷30=4
答えは「4分」となります。
「平均」の問題で面積図を使う
■[例]200ページの本を5日で読んだときの1日あたりの平均ページ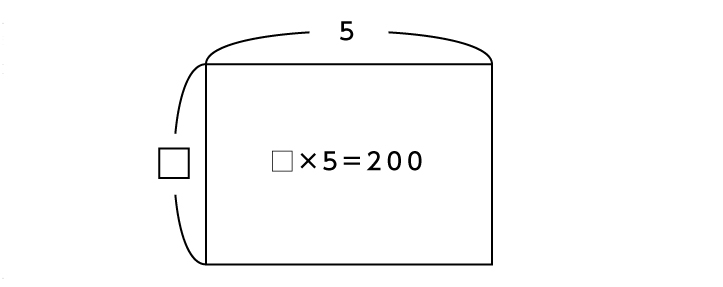
※画像は「面積図」を使った解き方のイメージです
※縦横の比率は、実際のものと異なります
平均×個数=合計
と考えると、
合計÷個数=平均
なので、
200÷5=40
答えは「40ページ」となります。
「濃度」の問題で面積図を使う
■[例]24gの食塩を使い20%の濃度の食塩水をつくった。食塩水は何gできるか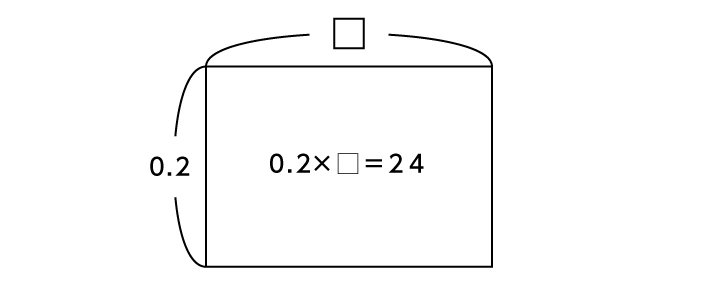
※画像は「面積図」を使った解き方のイメージです
※縦横の比率は、実際のものと異なります
濃さ×食塩水=食塩
と考えると、
食塩÷濃さ=食塩水
なので、
24÷0.2=120
答えは「120g」となります。
かけ算で見る「インド式計算」
ここまで、中学受験算数で学ぶ「面積図」について紹介しました。続いて一般的な筆算のやり方と、インド式計算について、かけ算を例に見ていきましょう。
一般的な筆算の方法
まずは、一般的な筆算の方法です。ここでは2桁同士のかけ算「14×12」を例にして計算してみます。
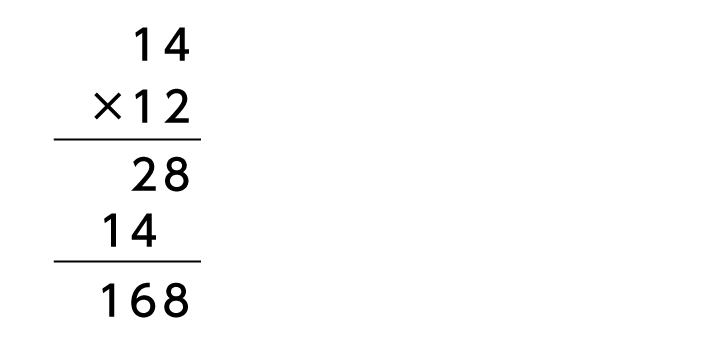
1の位は、2×4=8、2×1=2
10の位は、1×4=4、1×1=1
といった手順で位(くらい)をそろえて、たし算をして、「168」が答えとなります。
小学校で習う、ごく普通のやり方ですね。
インド式計算の場合
ではインド式計算の場合、どのように「14×12」を計算するのでしょうか。実は前述した「面積図」の考え方を使います。
■14×12
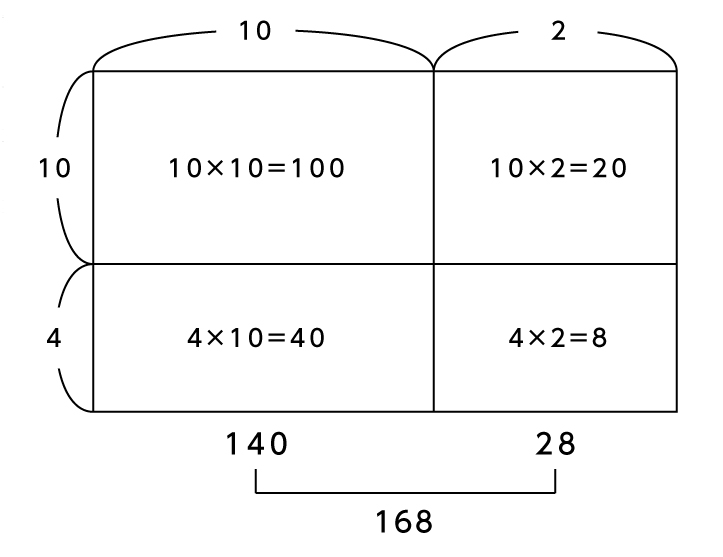
※画像は「面積図」を使った解き方のイメージです
※縦横の比率は、実際のものと異なります
「14」を縦軸の「10」と「4」に、
「12」を横軸の「10」と「2」に分けて考えています。
100+40=140
20+8=28
あわせて、答えは「168」となります。
2桁同士のかけ算は同じ要領で解くことができますね。
数の大きな計算にも使える
90台同士のかけ算でも「インド式計算」を使うと効率的に計算ができます。ここでは「97×94」を例に、一般的な計算方法とあわせてご紹介します。
97×94の一般的な計算方法
■筆算で解く
前述した、小学校で習う筆算を使った方法で計算してみましょう。
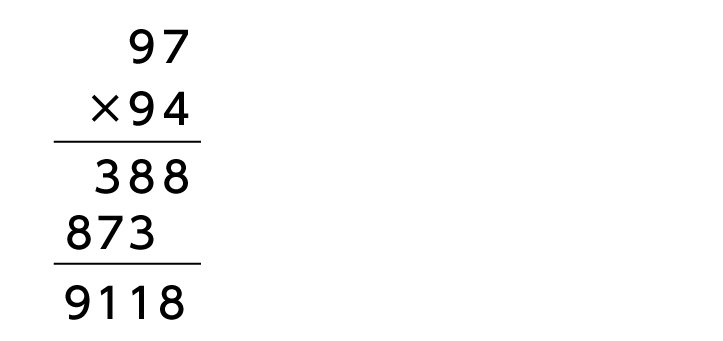
数が大きくなると、計算ミスが多くなりそうですね……。もう少し工夫をして、次のように解くこともできます。
■100を基準に解く
「10」や、「100」など、扱いやすい数字を基準にして計算するのは、よく使われる計算方法です。「97×94」の場合、「100」を基準にして次のように解くことができますね。
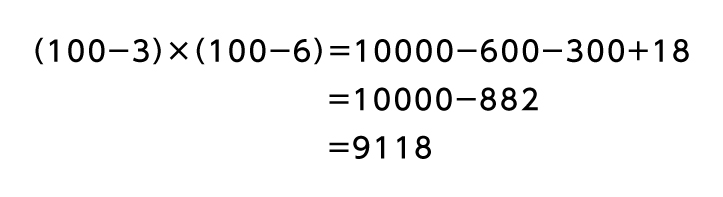
97×94をインド式計算で解く
インド式計算の場合、面積図を使って次のように解くことができます。
■97×94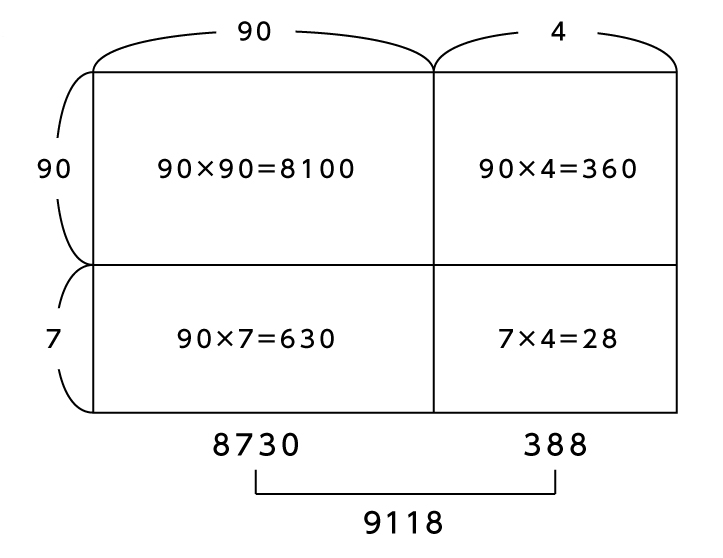
※画像は「面積図」を使った解き方のイメージです
※縦横の比率は、実際のものと異なります
「97」を縦軸の「90」と「7」に、
「94」を横軸の「90」と「4」に分けて考えています。
「8100+630=8730」
「360+28=388」
あわせて、答えは「9118」となりますね。
計算の工夫に役立つ「面積図」と「インド式計算」
中学受験算数では計算スピードを上げることと、計算ミスを防ぐことが必要です。今回紹介した、面積図と、インド式計算を使ったかけ算の計算方法も、解き方のひとつとして会得できるとよいでしょう。日々の学習でぜひ試してみてください。
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

