線分図を軽視するのは危険！ 中学受験をするなら低学年から線分図を練習しておきたい理由

「線分図」をご存知でしょうか？ 小学校では2年生で「テープ図」として学習するので、テープ図という名前なら知っているという方も多いかもしれません。テープ図はテープのような長方形を書き、線分図は数直線を書くというだけで、この2つに大きな違いはありません。

線分図を低学年から練習しておきたい理由

テープ図（線分図）は2年生の算数で少し触れるだけなので、中学受験に関係すると言ってもピンとこない方が多いと思います。それではなぜ線分図が中学受験に関係するかというと、線分図は中学受験算数では問題を解く重要なツールだからです。

中学受験算数の特殊算には線分図を使って解く問題がよくあり、なかには線分図を書けないと解けないものもあります。このため、低学年向けの中学受験向け問題集では、線分図から式をつくったり、逆に文章題を線分図にする問題が、1年生の段階ででてきたりします。

そこで今回は中学受験でも重要になってくる線分図の基本的な考え方や、低学年で使える問題集を紹介していきます。低学年のうちから線分図を意識した学習をすることは、中学受験算数の大きなアドバンテージになるので、普段の学習に活かしてください。

線分図とは

線分図とは、数量の関係を線分で表したものです。文章を視覚的に捉えやすくなるため、文章題を解く際のツールとして使われます。

例えば次のようなものが典型的な線分図です。

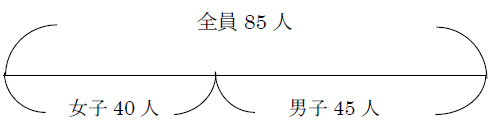
答え：85人

文章で読むだけではイメージしづらい数量の関係を、視覚的に捉えられるようになります。これこそ線分図が文章題を解く際のツールとして使われる理由です。

「文章題を解く際のツール」とはどういうことでしょうか。たとえば、下記の問題は簡単な和差算ですが、線分図を書くことで簡単に解くことができます。

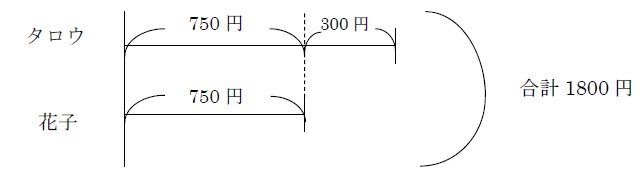
答え：750円

和差算は公式を使っても解けますが、線分図を書けば数量関係が視覚的にわかるので、公式を使わずとも解くことが可能です。

低学年でできる線分図の練習方法

中学受験において大切な線分図ですが、数量を線分に置き換える作業は抽象的なので、低学年の子供にとって線分図を書くのは容易ではありません。どのような練習をしたらよいのでしょうか。

難しく考えず、まずは小学校の足し算や引き算を線分図に表す練習から始めます。同時に小学校でならう簡単な文章題を線分図で表す練習をするといいでしょう。「数量関係は線分図に表せる」ということを理解し、まずは「線分図に慣れる」ことが第一です。

線分図が難しい場合は、テープ図で構いません。（テープ図のテープには太さがあるため、そこを分量としてとらえやすく、子供によっては線分図よりもわかりやすいようです）

線分図の練習におすすめの問題集

簡単な文章題を線分図で表すことができるようなら、線分図を重視した問題集を使用するのもおすすめです。

線分図を理解するのに役立つ問題集に、「サイパー思考力算数練習帳シリーズ 文章題 ～比較 順序 線分図 他～ 小2レベル」（認知工学）というものがあります。こちらは小学校より難しい文章題を線分図にして解く練習ができる問題集です。

この問題集では、文章題の下に線分図（またはテープ図）が書かれているので、まずは文章と線分図を見比べてリンクさせてみる練習から始めるとよいと思います。それができたら、線分図を隠して自分で線分図を書いてみると、より効果的です。

小2レベルをマスターしたら、同じシリーズの「文章題 ～和差算・ 分配算 小3レベル」にチャレンジしてみましょう。

この2冊をクリアできれば、低学年でできる線分図の基礎は問題なし。ここまでやれば多少なりとも中学受験算数の先取りにもなっているので、中学受験の勉強にスムーズに入っていくことができます。

思考力算数練習帳シリーズ（認知工学）
http://ninchi.sch.jp/cogtec/Arithmetic1.html

まとめ

「小学校ではあまり触れられないけれど、実は中学受験算数で重要なもの」の代表格が線分図です。低学年のうちから線分図の考え方に触れておくことで、中学受験算数の勉強がスムーズになります。中学受験をしない場合でも、文章を抽象的な作業で具体化する能力が向上することは間違いありません。

線分図を書くことは文章題を解く力にも繋がるので、「たかが線分図」と思わずに、普段の学習でも線分図を意識した取り組みをしていくことが大切です。

※記事の内容は執筆時点のものです