合成抵抗と電流の関係～電気回路の初級レベルから順に考えよう

合成抵抗は、一部で特殊な考え方を必要とします。そのため子供には、「まず基礎や初級レベルを完成させてから取り組む」よう伝えるのが得策だと思います。無用な混乱による時間のロスを防ぐためです。

ところが一般的に、中級の考え方というのは初級を包含します。いったん中級レベルの内容を身につけてしまえば、同じ考え方で初級にも適用できるはずです。今回は基本的な電気回路も含めて、「オームの法則」（電流＝電圧÷抵抗）という一貫した考え方で全体を眺めてみます。

合成抵抗とは電気回路の全体抵抗
～抵抗を直列につないだ場合の考え方

合成抵抗とは、まず「電気回路全体の抵抗」から「電気回路全体の電流」をもとめ、次に各個別の抵抗に流れる電流へと展開していく考え方です。なじみやすい直列つなぎ（すべて電池は1つ）から順に考えてみましょう。

合成抵抗の考え方～抵抗が1つの場合

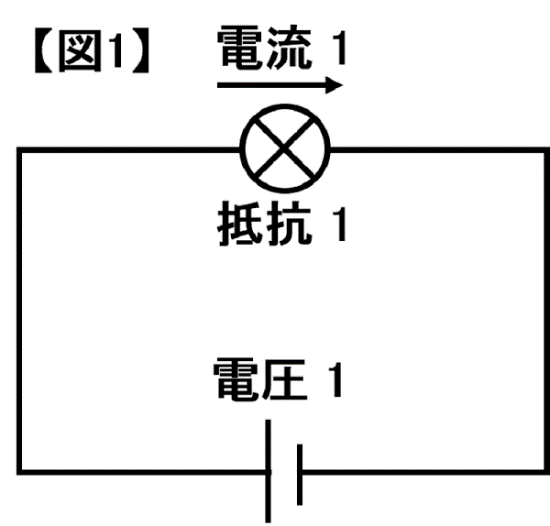初級レベルでは、【図1】の電気回路を基準にして比較で考えていきます。直列つなぎは単純で、電流の邪魔もの（抵抗）が増えるほど、電流は基準の量から減っていくという考え方です。

あえて【図1】について「オームの法則」で述べるならば、「電流＝電圧（1）÷抵抗（1）＝1」となります。あくまでも基準の電気回路ですから、特に違和感はないと思います。

合成抵抗の考え方～抵抗が2つの場合

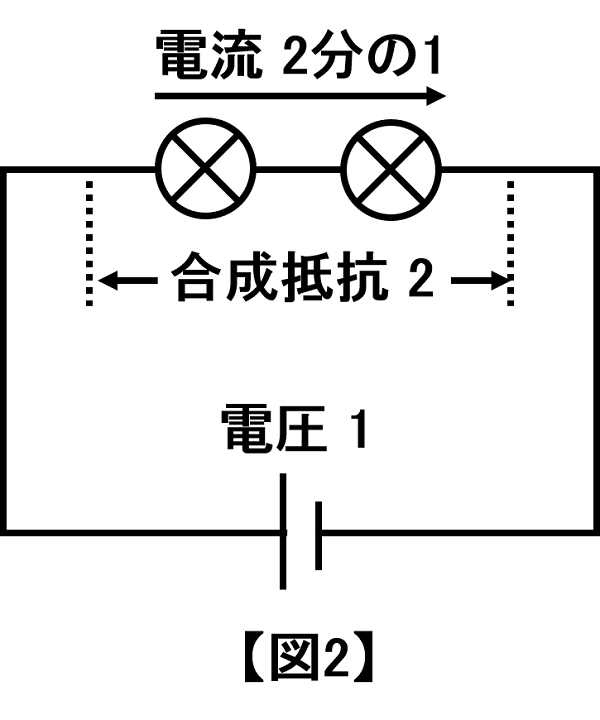抵抗が直列につながると、合成抵抗は「各抵抗の値」の和となります。【図2】では、「合成抵抗＝左の抵抗（1）＋右の抵抗（1）＝ 2」です。

よって「電流＝電圧（1）÷合成抵抗（2）＝\(\frac{1}{2}\)」。直列つなぎのため、各抵抗に流れる電流も「\(\frac{1}{2}\)」です。

ここまでは、初級で理解したように「邪魔ものが、基準となる電気回路の2倍だから、電流は\(\frac{1}{2}\)」と考えても特に問題はありません。

合成抵抗とは電気回路の全体抵抗
～抵抗を並列につないだ場合の考え方

直列つなぎの場合と大きく異なる点は、並列つなぎではブラックボックスの考え方を理解する必要があることです。この部分を乗り越えてしまえば、一気に視界が開けることでしょう。

合成抵抗の考え方～ブラックボックスの意味

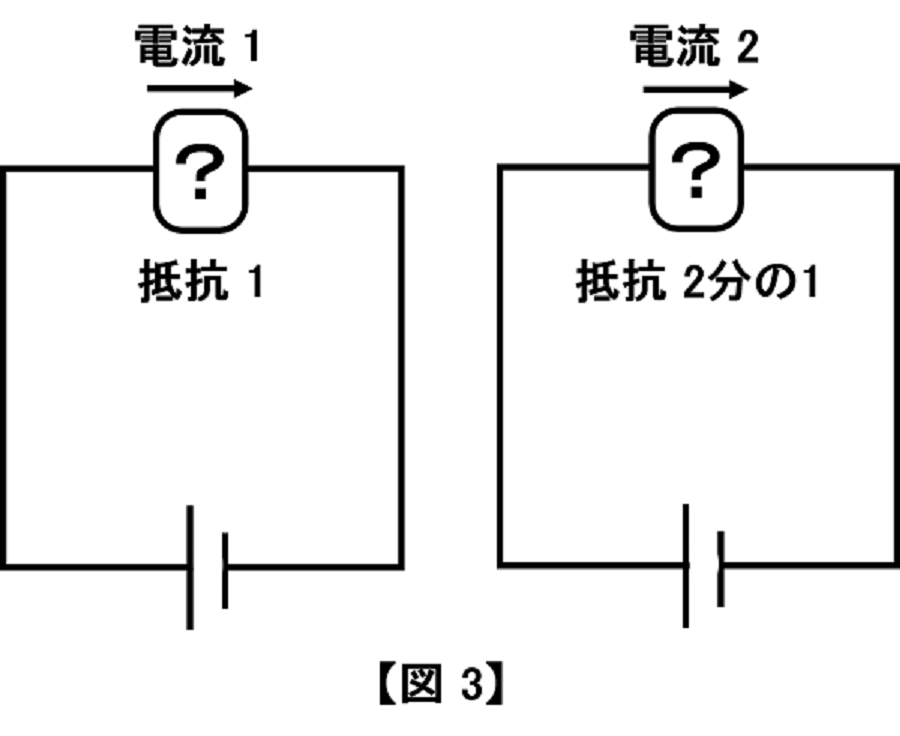ブラックボックスとは、中がどうなっているのか分からないということです。中の電気回路がどうであれ、 例えば【図3】（左）のように電流が「1」であれば、ブラックボックス全体の抵抗は「1」のはずです。

同様に【図3】（右）のように電流が「2」なら、ブラックボックス全体の抵抗は「\(\frac{1}{2}\)」です。では、ブラックボックスの中はどうなっているのでしょうか。

合成抵抗の考え方～抵抗が2つの場合

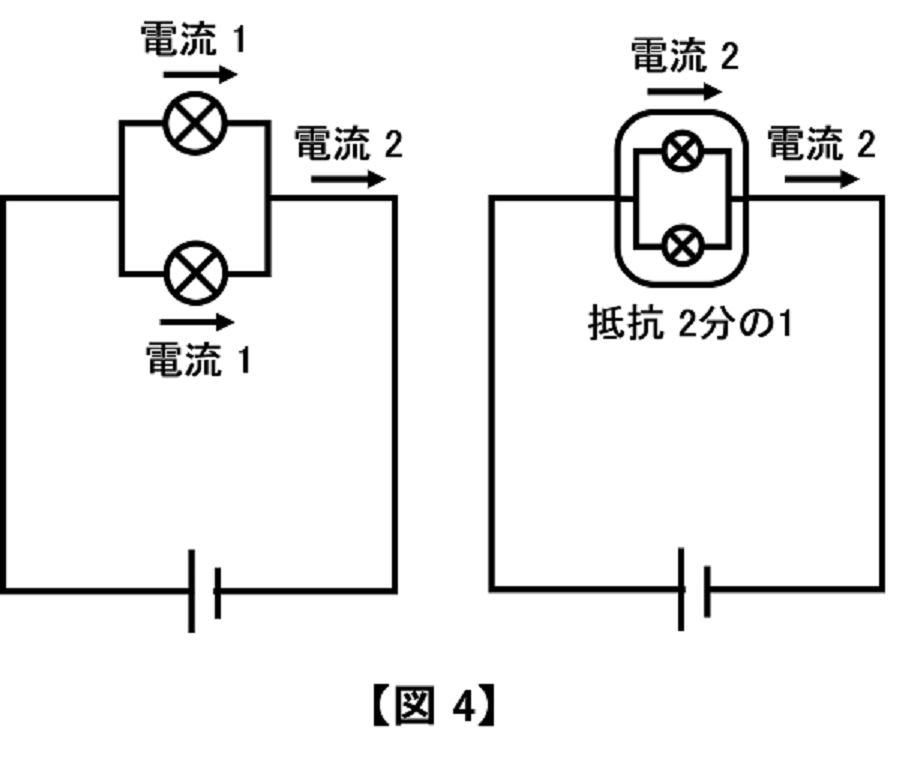初級では【図4】（左）を、「お互いに影響し合わない別々の回路が、2つ同時に存在する電気回路」と考えます。各抵抗に流れる電流は「1」ずつなので、電気回路全体に流れる電流は「2」となりました。

上記の結果「同じ抵抗2つを並列につなぐと、電気回路全体の電流が2倍になる」または「同じ抵抗2つを並列につなぐと、合成抵抗が半分になる」ことが判明します。

先ほどの【図3】（右）でも、電流が「2」抵抗が「\(\frac{1}{2}\)」となっているので、描かれていたブラックボックスの中身の一例としては「同じ抵抗2つの並列つなぎ」が挙げられるということです。

そこで以上の結論を、証明ずみの常識としてしまいます。中級では【図4】（右）のように、抵抗2つの並列つなぎは合成抵抗が\(\frac{1}{2}\)となるので、「電気回路全体の電流＝電圧（1）÷抵抗（\(\frac{1}{2}\)）＝2」と考えます。

合成抵抗とは電気回路の全体抵抗
～直列と並列を合わせた場合の考え方

ここまでは初級の電気回路であるため、なぜ回りくどい考えをするのか疑問に思われるかもしれません。ところが以降の電気回路では、合成抵抗の考え方を採用しなければ解くことができません。

合成抵抗の考え方～直列と並列（その1）

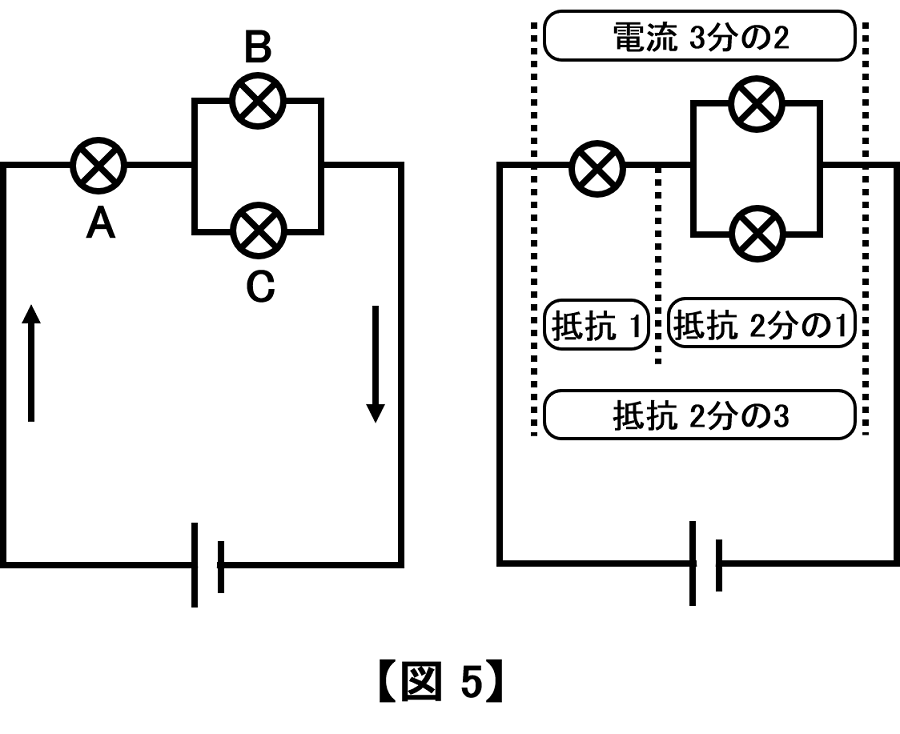【図5】（左）を初めて見た子供は全員が、「2つの異なる回路が同時に存在している」と考えます。並列つなぎと同様だと思ってしまうからです。

ところが電流はAを通ってからBとCに分岐して再び合流しますから、A・B・Cで一体の電気回路です。もはや合成抵抗で考えるしか方法はありません。

【図5】（右）に示すように、「抵抗1」と「抵抗\(\frac{1}{2}\)」の直列つなぎなので、「合成抵抗」＝「1」＋「\(\frac{1}{2}\)」＝「\(\frac{3}{2}\)」です。よって「電気回路全体の電流＝電圧（1）÷抵抗（\(\frac{3}{2}\)）＝\(\frac{2}{3}\)」で、各抵抗に流れる電流は「A：\(\frac{2}{3}\)」「B：\(\frac{1}{3}\)」「C：\(\frac{1}{3}\)」となります。

合成抵抗の考え方～直列と並列（その2）

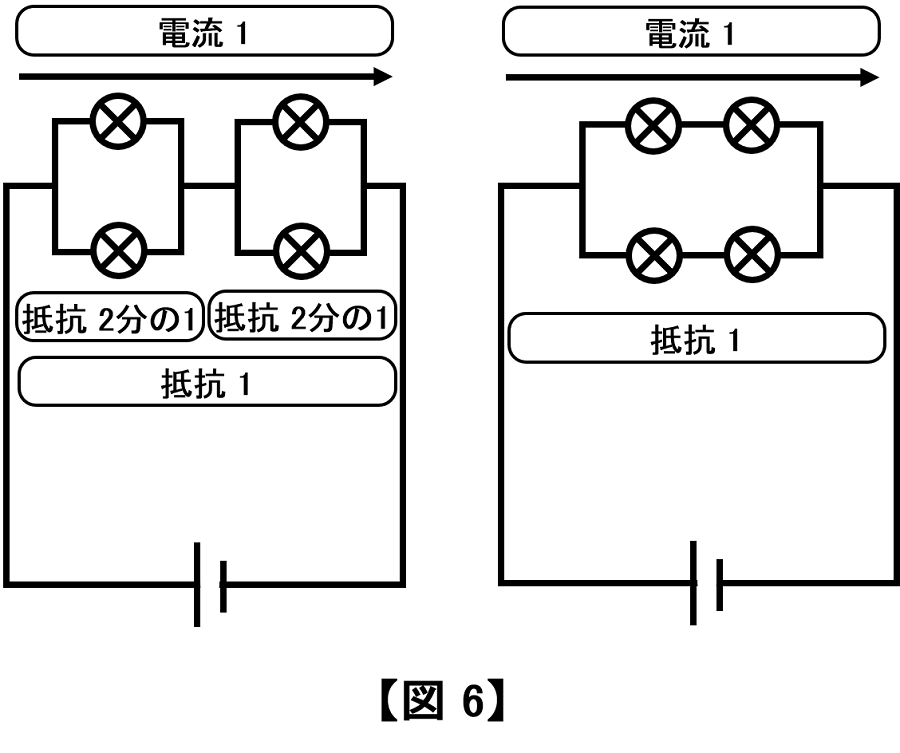【図6】（左）は「抵抗\(\frac{1}{2}\)」と「抵抗\(\frac{1}{2}\)」の直列つなぎなので、「合成抵抗」＝「\(\frac{1}{2}\)」＋「\(\frac{1}{2}\)」＝「1」です。よって「電気回路全体の電流＝電圧（1）÷抵抗（1）＝ 1」で、各抵抗に流れる電流はそれぞれ「\(\frac{1}{2}\)」ずつとなります。

【図6】（右）は「抵抗2」と「抵抗2」の並列つなぎなので、合成抵抗は1、「電気回路全体を流れる電流＝電圧（1）÷抵抗（1）＝ 1」、各抵抗を「\(\frac{1}{2}\)」ずつ電流が流れます。

まとめ

◎並列つなぎのブラックボックス的な考え方に慣れましょう。
◎抵抗を直列につなぐと、合成抵抗は各抵抗値の和です。
◎同じ抵抗を並列につなぐと、合成抵抗は半分になります。
◎合成抵抗をもとに、「オームの法則」から電流をもとめます。

※記事の内容は執筆時点のものです