
【算数】差集め算は「本質」の理解が大切! とりちがえ問題の解法も紹介
中学受験の算数で、偏差値が伸び悩んでしまう原因のひとつ。
それは、やり方だけを覚えてしまって「本質を捉えていない」ということです。
やり方を丸暗記すると意外と解けてしまう。
でも、応用となると急に解けなくなってしまう……。
これは本質を理解しておらず、やり方だけを覚えてしまっているからかもしれません。基本問題はできるのに、応用問題になると途端にできなくなってしまう場合は特に注意しましょう。
今回は「差集め算」と、その応用ともいえる「とりちがえ問題(とりちがえ算)」について、中学受験生が本質から理解できるように解説します。
Contents [hide]
差集め算とは
差集め算とは、“差を集める”ことが解法となっている問題です。
これだと抽象的でわかりにくいので、具体的な例を使って解説します。
<例>
50円切手と80円切手を5枚ずつ買ったら、その代金はいくらでしょうか?
50円切手を5枚買ったら250円、80円切手を5枚買ったら400円ですね。差額は150円です。
ここで大切なポイントがひとつ。
50円切手と80円切手の差額は30円。
でも5枚買うとなると、その差額は150円。
つまり、50円切手と80円切手の差額30円を全部集めると、全体の差額150円になるということ。
これが“差を集める”、つまり「差集め算」という名前の由来です。

1個1個の差を全部集めると全体の差になるので、イコールでむすんであげよう! ということですね。
差集め算を解くときは、まずはこの本質を押さえましょう。

差集め算の解き方
本質を知れば、差集め算の解法は“超シンプル”です。

では、実際に問題を解いてみましょう。

STEP1:問題文を読んで線分図を書く
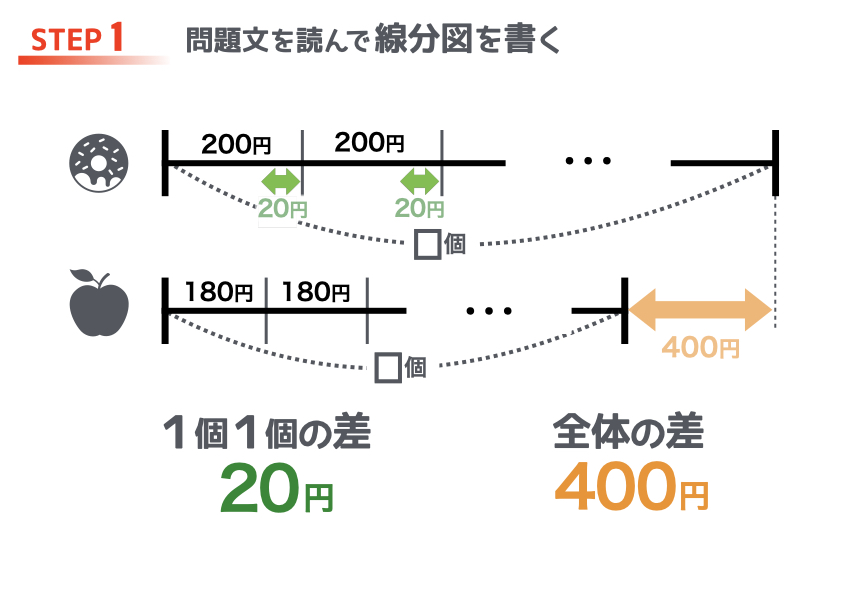
線分図を書くのは、「1個1個の差」と「全体の差」を整理するためです。
頭の中で整理できる子は省略しても良いですが、最初は線分図でまとめるのがおすすめです。
ドーナツとリンゴの1個1個の差額はもちろん「20円」。
全体の差額は、問題文から「400円」とわかりますね。
STEP2:「1個1個の差の合計」と「全体の差」をイコールでむすぶ

ここまで来れば簡単です。
1個1個の差の合計と、全体の差をイコールでむすんでしまえば良いのです。
20円✕□=400円
計算の結果、□=20であることがわかります。
答え:20個
差集め算の本質は理解できたでしょうか?

差集め算の出題パターンは、以下の記事で紹介しています。
中学受験:差集め算とは? 基本問題はできるのに応用問題ができない理由
とりちがえ問題
差集め算の応用問題と位置づけられる「とりちがえ問題(とりちがえ算)」について解説します。
具体的には、以下のような問題です。

差集め算のように1個1個の差はわかりますが、次のふたつの要素が加わっていることが違いですね。
- 買う個数を間違えてしまった
- 予定からずれてしまった
ちょっと見ただけでは「差集め算ではない」と感じてしまう問題文ですが、よく読むと、差集め算の要素がしっかりと散りばめられています。
- 一つひとつの差がわかる(ドーナツとリンゴの価格の差)
- 全体の差がわかる(予定より200円やすくなった)
差集め算の解法で解けそうな気がしてきましたか?
でも、“とりちがえ”が絡む場合には、ちょっとした工夫が必要です。
とりちがえ問題の解き方
とりちがえ問題を解くステップを紹介します。
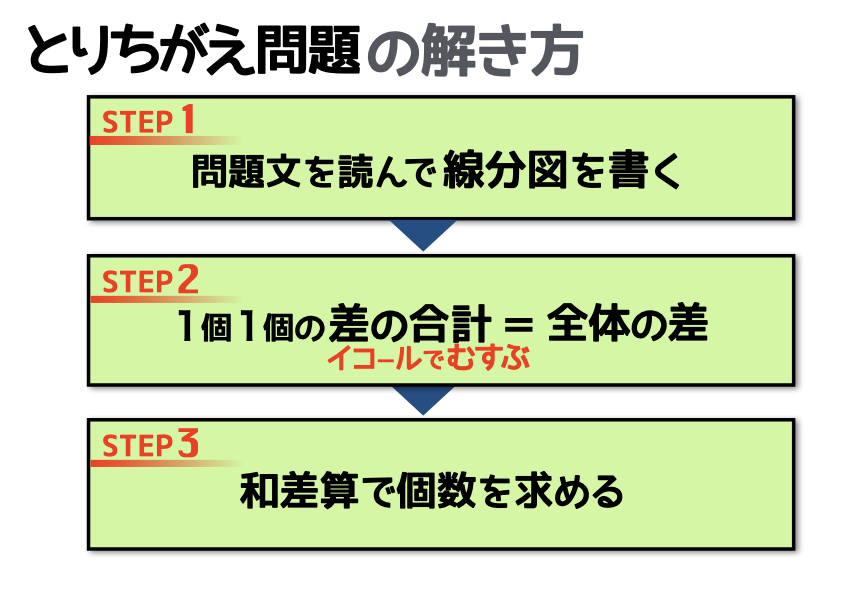
一般的な差集め算の解法に、STEP3(和差算で個数を求める)が増えていますね。
線分図を書くSTEP1についても、ちょっとした“ヒネリ”が必要です。
百聞は一見にしかず。
さっそく問題を解いていきましょう。

STEP1:問題文を読んで線分図を書く
最初は、問題文を読み解いて整理するステップです。
線分図を書くまえに、問題文から読み取れるイメージを整理してみましょう。
ポイントは次のふたつです。
- ドーナツとリンゴを買う数を“さかさま”にしてしまった
- 全体の金額が200円ほど減ってしまった

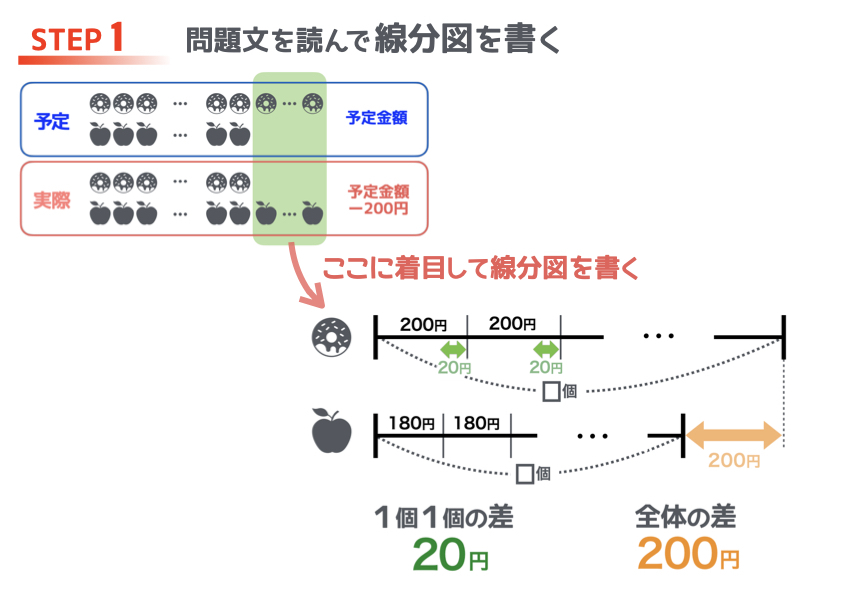
では、上の図を線分図にしてみましょう。
このときのポイントは「個数の差」に着目すること。
200円のドーナツと、180円のリンゴをそれぞれ何個買ったかわかりませんが、全体の差額が200円ということはわかります。
まずは、この部分だけの線分図を書いてみましょう。
STEP2:「1個1個の差の合計」と「全体の差」をイコールでむすぶ
次のステップは差集め算の本質、つまり「1個1個の差の合計」と「全体の合計」をイコールでむすぶステップです。
ドーナツは180円、リンゴは200円なので、1個1個の差は「20円」。
10個なら200円、100個なら2000円、1000個なら20000円ですね。

STEP3:和差算で個数を求める
今回の問題はリンゴの個数がいくつだったかを求められているので、最後の仕上げが必要です。
ここで登場するのが「和差算」です。
ドーナツとリンゴの合計は20個、ドーナツとリンゴの数の差は10個ということから、それぞれの個数を知りたい場合は和差算のテクニックを使うのが有効です。

上記の計算をしっかり解けると、もともとの購入予定はドーナツが15個、リンゴが5個であることがわかりますね。
和差算の解法は以下の記事で紹介しています。
中学受験:和差算とは? 線分図の“3つの本質”で簡単に解ける
まとめ
差集め算の解き方を紹介しつつ、その応用ともいえる「とりちがえ問題(とりちがえ算)」についても解説しました。
算数の成績がずっと伸び悩んでいる子の場合、算数の問題に対する理解度が足りていないことが原因の可能性があります。
やり方だけ丸暗記したので基本問題はできる。
でも、応用問題には太刀打ちできない……という状況ですね。
差集め算が苦手な子は多いですが、まずはその本質を理解することが大切です。
今回の記事を繰り返し読みつつ、差集め算を攻略しましょう!

※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

