濃度計算の公式はどうして成り立つの？ 食塩水の問題を割合として理解しよう

中学入試の算数や理科では、食塩水の濃度計算がよく出ます。これらの問題を解くとき、「食塩水の重さ×濃度＝食塩の重さ」という公式が便利です。しかし、この公式をただ丸暗記しているだけだと、自分が何をしているのかがわからなくなり、応用も利きません。そこで今回は、この公式について詳しく解説した上で、実際に公式を使って問題を解いていきます。

公式の成り立ちを理解しよう

濃度計算の公式を使う前に、「濃度とは何か？」を理解した上で、どうして公式が成り立つのかを考えてみましょう。

濃度は溶液中の溶質の割合を表す

食塩水のように、ある物質が溶けている液体を溶液といいます。液体が水である溶液は特に水溶液と呼ばれます。溶液に溶けている物質が溶質、溶質を溶かす液体が溶媒です。

濃度は溶液中の溶質の割合です。濃度の表し方にはいろいろありますが、中学受験では、溶液の重さをもとにしたときの溶質の重さの割合を百分率で表します。

このことがわかっていれば、次の【問1】は簡単に解けるはずです。

溶液の食塩水300gが100％で、20％は100％の\(\frac{1}{5}\)倍なので、300gを\(\frac{1}{5}\)倍した60gが食塩の重さです。また、食塩水について割合の100％を3倍すれば重さの300gになることに着目して、食塩についても割合の20％を3倍すれば重さの60gを求められます。濃度が割合であることを理解していれば、わざわざ公式を使うまでもありません。

濃度計算を線分図で考えてみよう

【問1】を線分図で考えてみましょう。食塩の重さを□gとすると、線分図は次の通りです。濃度は百分率ではなく小数で表しました。

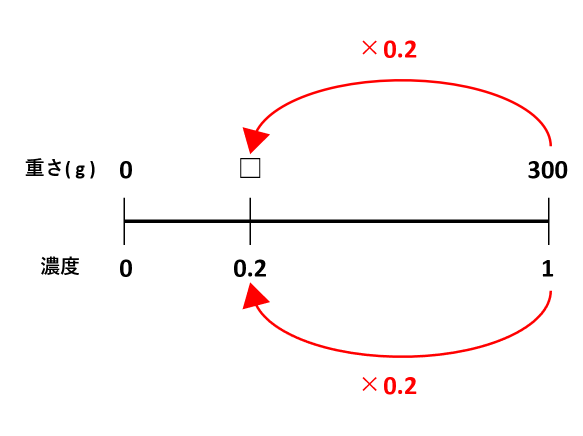
割合は1（100％）に0.2をかけると0.2（20％）になるので、重さにもついても300gに0.2をかけて□gを求められます。したがって、□＝300×0.2＝60（g）が答です。

300×0.2＝60の式は「食塩水の重さ×濃度＝食塩の重さ」です。線分図を描いてみれば、濃度計算の公式が成り立つことを理解できるでしょう。また、濃度計算の公式を線分図で表せることを覚えていると、「公式を忘れた」という場合でも安心です。