中学受験の「面積比」は2種類 似ていても性質が全く異なるので注意！

「面積比」とひとことで言っても多くの出題パターンがあります。中学の入試問題に出てくる全ての問題をパターン化するのはとても難しそうです。しかしながら、多くの面積比の問題に共通する基本要素があることは事実です。

本記事では面積比の問題を解くための基本要素を扱いたいと思いますが、私の息子が面積比を勉強していて陥った大きな間違いがありました。それが「面積比には性質の違う2種類が存在する」という根本的なことだったのです。息子が陥った間違いを交えながら面積比の基本要素を紹介します。

性質の異なる2種類の面積比

中学受験ではよく「面積比」という用語が出てくるのですが、そもそも成り立ちが異なる2種類の「面積比」が存在します。

ひとつは「三角形の面積の公式を利用した面積比」、もうひとつは「相似を利用した面積比」です。

この2つを混同すると「大ヤケド」することになります。同じ面積比という言葉で子供が混同しないようにすること大切です。

三角形の面積の公式を利用した面積比

ひとつめの「面積比」は三角形の公式を利用したものです。2つの三角形があるとします。高さが同じであれば、面積比は底辺の長さの比と等しくなます。そして底辺の長さが同じであれば、面積比は高さの比と等しくなりますね。これは単純に「底辺×高さ÷2」という三角形の面積の公式を利用したものですね。

相似である図形を利用した面積比

ふたつめの「面積比」は相似を利用したものです。相似とは、図形を縮小したり拡大したりした関係のことで、辺の長さの比を相似比と言います。相似である2つの三角形があるとします。この場合は、面積比は相似比の2乗に等しくなります。面積の公式を利用した面積比と異なるものです。これを混同してしまっては大変です。

2つの面積比の違いを整理する

2つの面積比の違いを整理してみましょう。成り立ちがそもそも違うので、性質も異なります。一般的に面積比を使う問題は、2つの図形の辺の長さの比と面積比の関係を利用して問題を解きます。辺の比から面積比を出せるようになることが重要です。

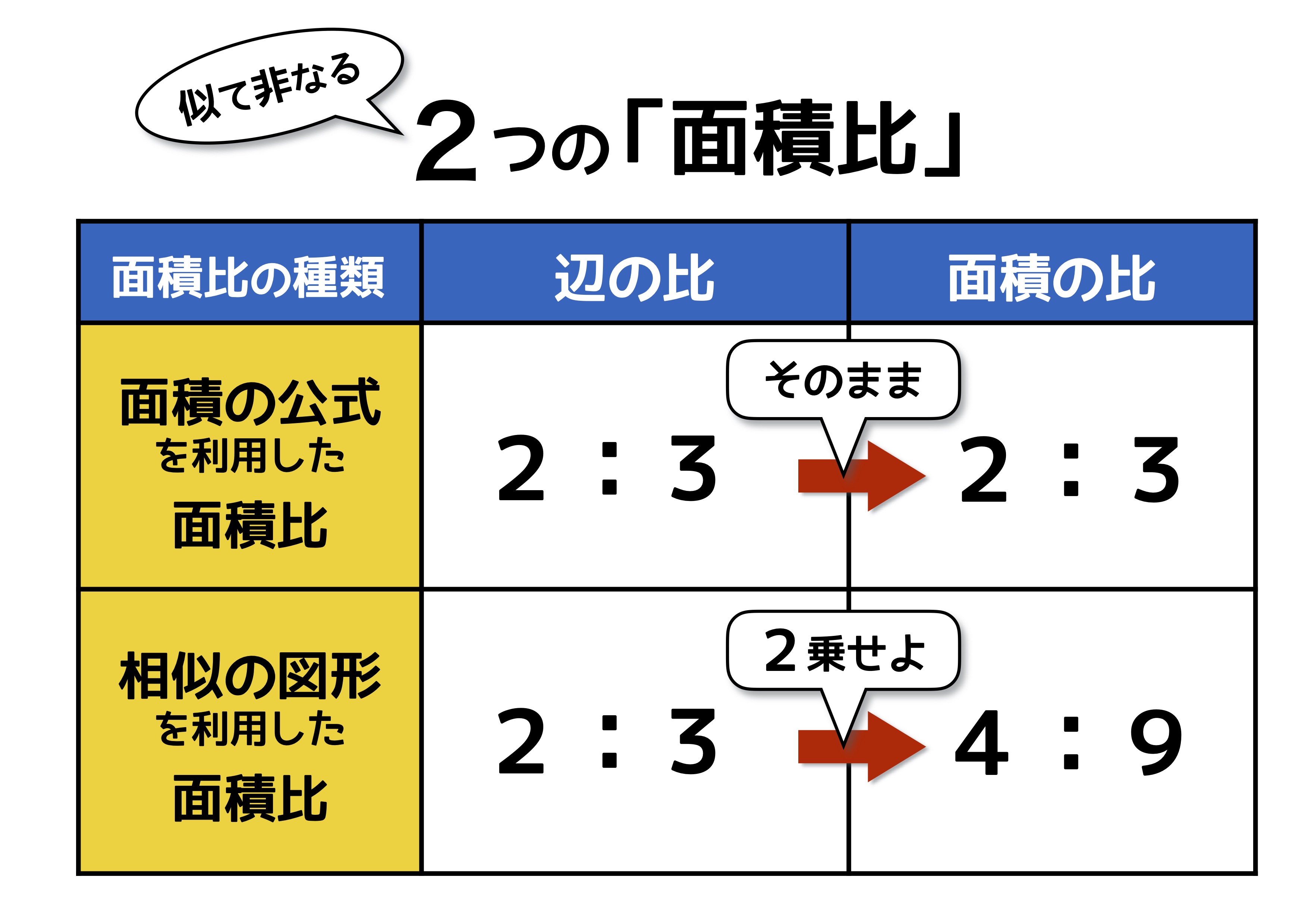
面積比の4つの具体例

2つの面積比に違いがあることを理解したところで、それぞれの具体的な例をおさえていきましょう。冒頭でも書いたとおり面積比の問題は実に多彩で、全ての問題をパターン化するのは難しいため、多くの中学入試の問題で必要となる4つの具体例をピックアップしました。

［1］三角形の高さが共通――面積の公式を利用した面積比

中学入試でよく出題される形です。青い三角形と赤い三角形は高さが同じなので、面積比は底辺の長さの比、つまり3:4になります。よく出題されていますから、この形はしっかりおさえましょう。

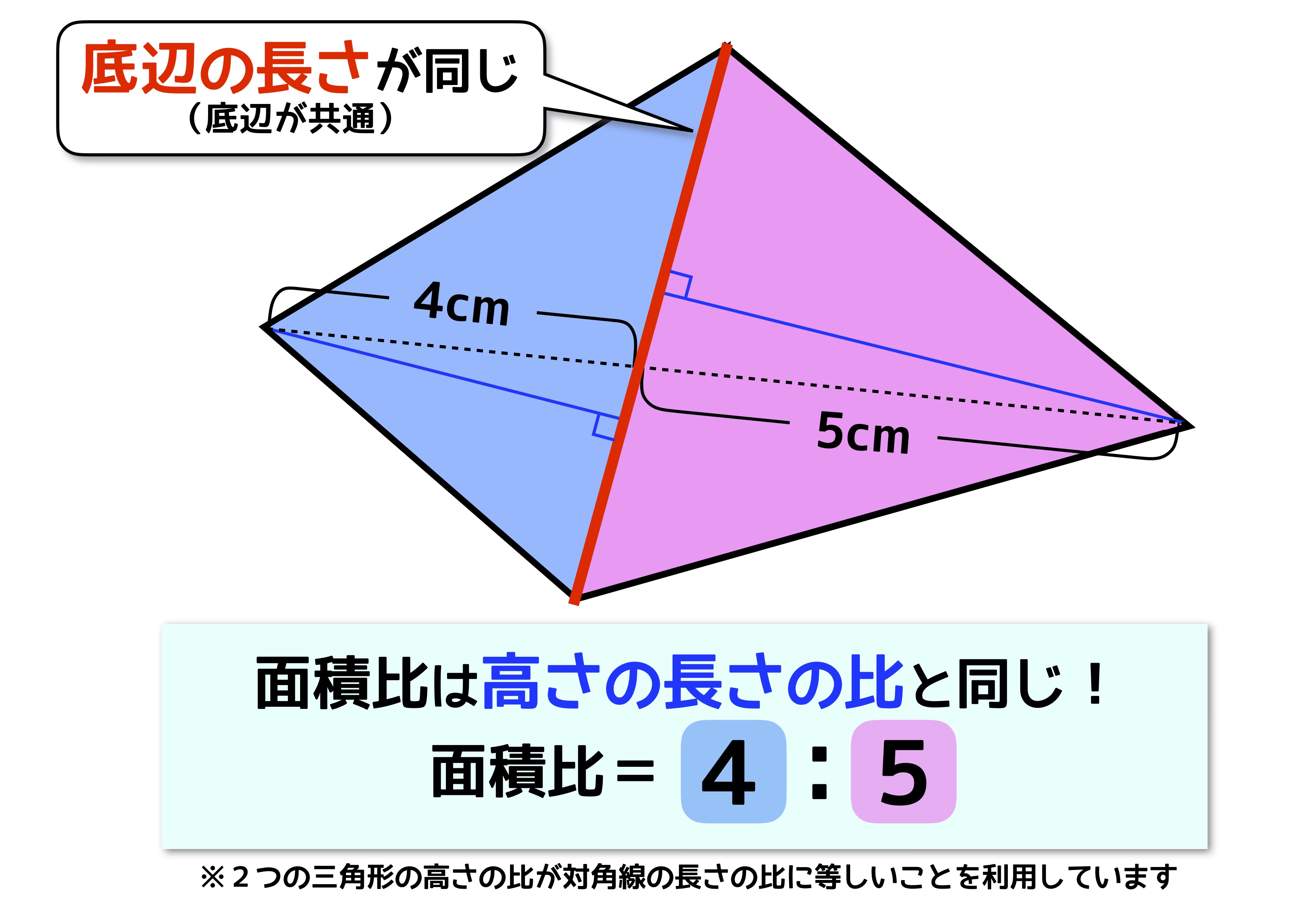
［2］三角形の底辺が共通――面積の公式を利用した面積比

底辺が同じ場合はどうでしょうか？ その場合は高さの比がそのまま面積比になります。青い三角形と赤い三角形の面積比は4:5になります。注意してほしいのは、図に書かれている「4cm」と「5cm」が高さではなく対角線を分割したときの長さだということ。このとき、高さを示す線を青で引いてみるとわかりますが、対角線の分割比は高さの比と同じであることがわかります。この形（底辺が同じ場合）の図形を見たら高さの比は対角線の分割の比と考えてよいでしょう。

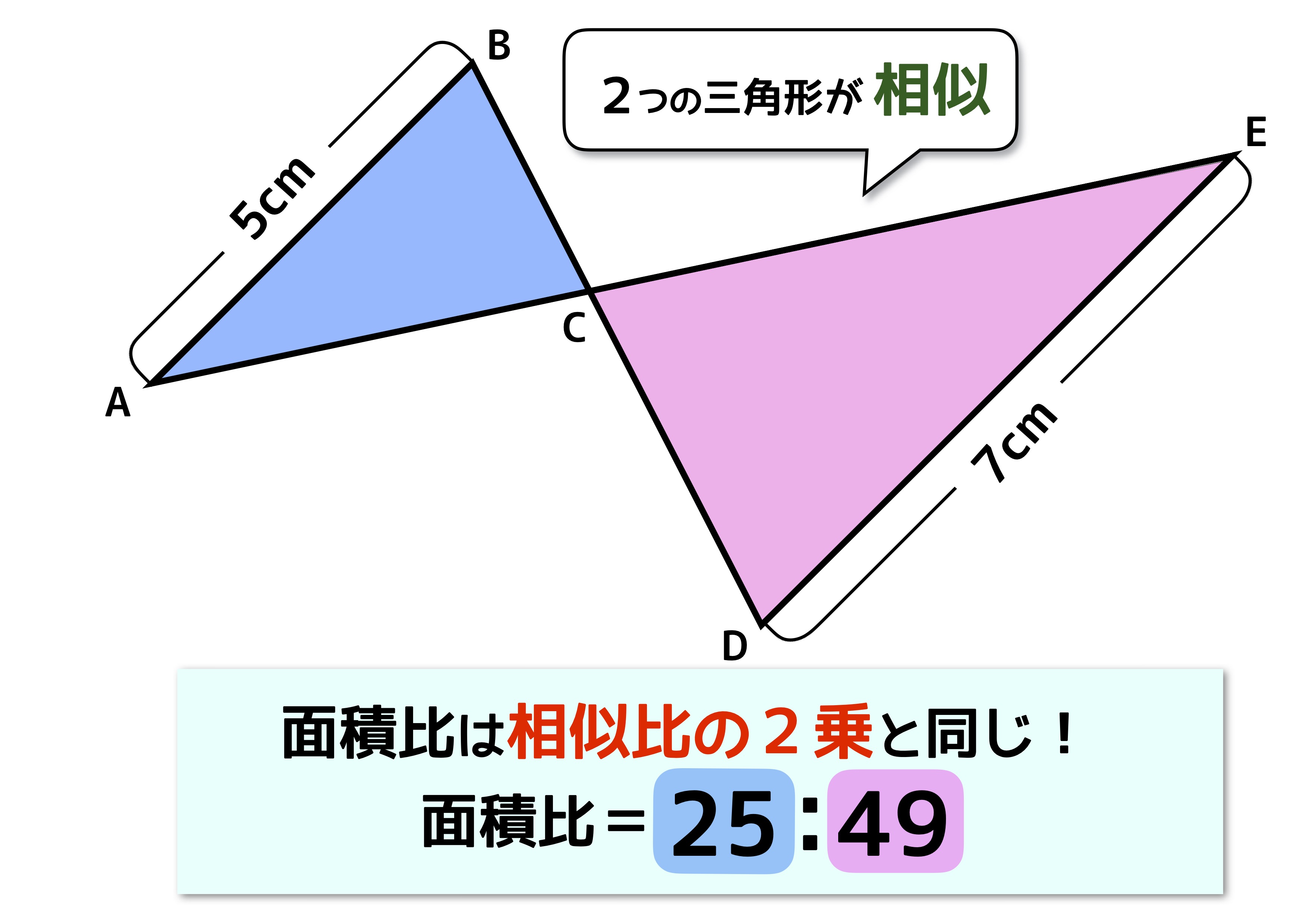
［3］リボン形の相似――相似の図形の図形を利用した面積比

この形も入試では本当によく出題されますね。このリボンのような形は覚えてしまいましょう。辺ABと辺DEが平行のとき、青い三角形と赤い三角形は相似なので、面積比は相似比の2乗で25：49になります。5：7ではありませんので間違えないように！

［4］相似の図形の利用――ピラミッド形の相似

最後はピラミッド形の相似です。こちらも図では省略していますが辺BCと辺DEは平行です。この図は、青い三角形ADEと赤い三角形ABCが重なっているものなので注意しましょう。そして青い三角形と赤い三角形の面積比は相似比の2乗となりますので1：4になります。リボン形相似と同様、面積比は1：2ではないので注意が必要です！

まとめ

中学受験で登場する面積比。同じ面積比という言葉を使っていても性質の全く異なる面積比があることに着目し、4つの具体例と共に面積比の問題を解くための基本要素をご紹介しました。

私の息子が混同してしまったポイント、それは「面積の公式を利用した面積比」と「相似を利用した面積比」は似て非なるものであり、性質が大きく異なるというポイントです。この部分を混同してしまうと、大きな失点の原因になり得るので注意して子供と確認しましょう。

※記事の内容は執筆時点のものです