循環小数と分数の関係を考えよう！ 規則性に注目すると小学生でも理解できる

0.3333…や1.57878…のように、同じ数字が無限にくり返される小数を「循環小数」といいます。循環小数は高校数学で本格的に学びますが、中学受験算数でも出題されることがあります。

循環小数と分数の関係を理解したうえで、中学受験でよく出る問題にチャレンジしてみましょう。

循環小数を分数で表してみよう

小数点以下に数字が無限に並ぶ小数を「無限小数」といいます。無限小数のうち、0.3333…は3が無限にくり返されるので循環小数です。一方、円周率の3.14159…は同じ数字の繰り返しがないので循環しない無限小数です。循環小数と循環しない無限小数には、分数で表せるかどうかの違いもあります。

0.3333…を分数で表してみよう

たとえば、0.3＝\(\frac{3}{10}\)、0.33＝\(\frac{33}{100}\)のように、無限小数ではない小数（有限小数）は分数で表せます。実は、0.3333…などの循環小数も分数で表すことができます。実際に分数で表してみましょう。

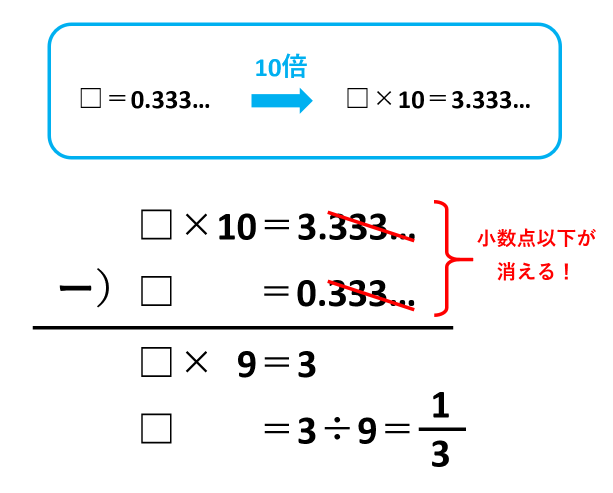
□＝0.3333…とします。これを10倍すると、□×10＝3.3333…となります。□×10＝3.3333…から□＝0.3333…を引くと、□×10－□＝3.3333…－0.3333…です。＝の左側は□10個から□1個を引くので□×9となり、＝の右側は小数点以下が0.3333…で同じ形なので3だけが残ります。□×9＝3なので、□＝3÷9＝\(\frac{3}{9}\)＝\(\frac{1}{3}\)になりました。

循環小数を分数で表すコツは、小数点以下を同じ形にすることです。

1.57878…を分数で表してみよう

今度は1.57878…を分数で表してみましょう。□＝1.57878…とするところまでは0.3333…と同じです。しかし、単純に10倍するだけだと、□×10＝15.78787…となって、□＝1.57878…と小数点以下が同じ形になりません。そこで一工夫します。