
【中学受験算数】「回転体が苦手」を克服するための勉強法
Contents [hide]
「感覚的な理解」よりも「実際に解ける」が大切
回転体が苦手という生徒をたくさん見てきました。さまざまな原因がありますが、苦手意識のある生徒が異口同音に言うのが「回転体のイメージができない」ということ。そこで今回は、イメージしづらい回転体を得意にするためのアプローチをまとめました。
回転体は「平面で考える」がコツ
まずは立体をイメージして、そこから問題が解けるようになっていく……と思っている人が多いように感じます。知らず知らずのうちに「立体のイメージができないと解けない」と思い込んでいませんか?
立体をイメージできることよりも、平面にして考えることができるほうが大切なのです。
「立体」ではなく「平面」で考える
立体は三次元です。平面は二次元です。高次元になればなるほど、問題は難しくなります。立体問題が苦手な子供が多いのはそういう意味では自然なことでしょう。
数学の考え方の鉄則で、「高次元のものは低次元で考える」というものがあります。
抽象的なものは、具体的なもので、次数の高いものは、次数を下げる、などなど、中学生以降も大変重要になる考え方です。
大切なのは「複雑で直感的に理解できない」ものを、自分の理解できる範囲に誘導して考える姿勢です。
線対称を極める
回転体を平面で理解するためには、まず線対称を理解する必要があります。
まずは点を線対称に移す方法です。細かい説明は不要ですね。下の図のような移動を線対称移動といいます。
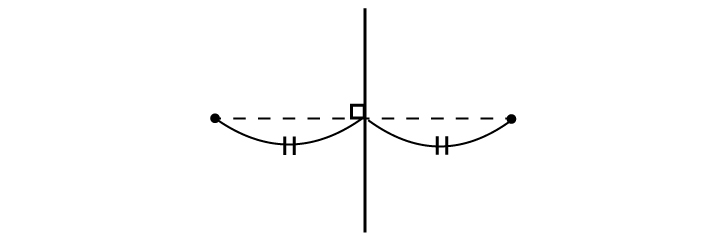
点を線対称移動できるようになったら、次は多角形を線対称移動しましょう。「多角形=点を直線でつないだもの」です。多角形の図形そのものを移動させるという意識ではなく、角の点を対象に移動させることで、多角形を移動させると考えましょう。
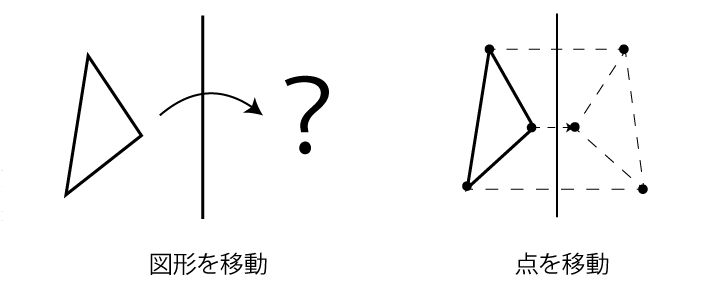
回転体には直接関係がないことが多いですが、図形の感覚を磨くために、最後に円を移動させてみましょう。円は「中心と半径」で決まりますね。中心を点対称移動させて、同じ半径の円をかけばOKです。
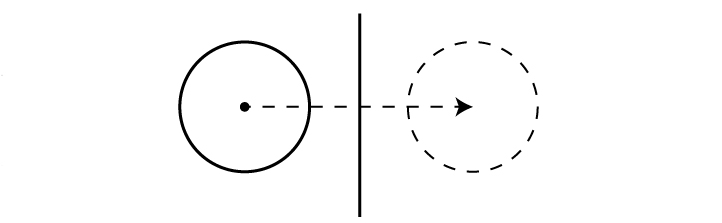
ルールを守れば、立体が分かる!?
これで回転体を描くための準備が整いました。実際に描くためのルールをみていきましょう。
回転体を描くためのルール
回転体を描くためのルールは下の2つです。
①図形を回転軸対称に移動させる。
②対応する点で「円」を描く。
たったこの2つを守るだけで、回転体を正確に描くことができます。具体的にみていきましょう。まずはもっとも簡単な三角形の回転体。
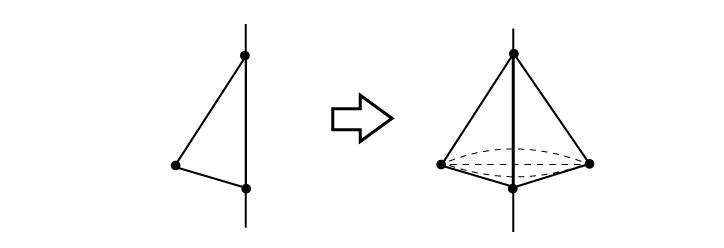
円を描くところは見取り図になるように、「歪めて」描くことがポイントです。正円ではなく、少しつぶしたような円を描くと、立体らしくなってきますね。
次のように回転軸と図形が離れている場合でも、ルールに沿って描いてみれば簡単です。
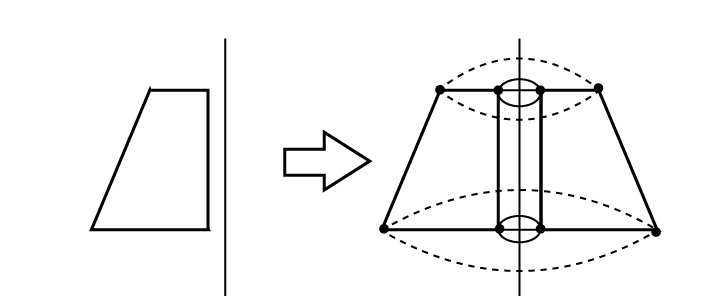
とにかくたくさん描く
以上のルールを守りながら、とにかくたくさん回転体の見取り図を描いてください。描く中で自然と立体感覚が育ってきます。たくさん描く練習は楽しくできるとよいです。
問題として出題されるような図形から離れて、遊び感覚でたくさん描く練習ができるとよいでしょう。
たとえば、次のような回転体。
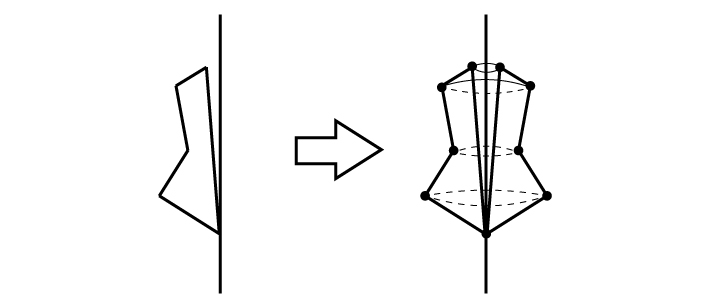
こういう問題の方が逆に楽しく、「きれいに描いてやろう」とやる気になりますよね。親子で出題しあって楽しめるとよいですね。
ルールをシンプルにすれば、回転体は必ず理解できる
立体感覚は大変重要ですが、感覚がなくても問題は解けます。そして解いていくなかで、立体感覚が育ってくることも多いのです。
回転体に苦手意識のある場合は、ぜひ本記事を参考に、たくさん回転体を描いてみるところから始めてみてください。
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

