
推理算がおもしろい! 算数が苦手な小学生でも思わずハマる楽しい問題5選
算数というと計算のイメージがあります。しかし、中学受験算数のなかには、計算力を必要とせず、条件を整理しながら正解を導くタイプの「推理算」があります。
そんな推理算のなかから、有名な問題とその解き方を紹介します。算数が苦手な小学生でも思わずハマる問題ばかりです。名探偵になったつもりで、頭の体操を楽しみましょう。
Contents [hide]
- 推理算で大切な条件整理
- 思わずハマる楽しい推理算5選
- 推理算[1]偽物の金貨はどれ?
- 推理算[2]誰が嘘つきかな?
- 推理算[3]向かいには誰が座るの?
- 推理算[4]背の高い順に並ぼう!
- 推理算[5]魔方陣を完成させよう!
- 推理算で算数の本質を学ぼう
推理算で大切な条件整理
推理算は、偽物の金貨を見つけたり、嘘つきを発見したりと、まるで探偵小説に出てきそうな問題ばかりです。これらを考えるうえで、与えられた条件を整理することが必要となります。推理算に限らず、算数では、計算以上に条件整理が大切です。
思わずハマる楽しい推理算5選
有名な推理算の問題を解いてみましょう。紙と鉛筆を用意して、図や表などを描きながら考えることをおすすめします。
推理算[1]偽物の金貨はどれ?
9枚の金貨があります。このうち1枚が偽物で、偽物は本物よりも軽いとわかっています。天秤で重さをはかって偽物を見つける場合、最低何回はかればよいですか。
まずは、9枚の金貨を3枚ずつのグループA、B、Cにわけます。そして、AとBを天秤の右と左の皿に載せます。偽物が軽いとわかっているので、以下のことがわかります。
・右の皿が高くなった。 → Aに偽物がある。
・左の皿が高くなった。 → Bに偽物がある。
・左右でつり合った。 → Cに偽物がある。
次に、偽物があるとわかったグループの3枚のうち、2枚を天秤の右と左の皿に載せると、以下のことがわかります。
・右の皿が高くなった。 → 右の皿の金貨が偽物。
・左の皿が高くなった。 → 左の皿の金貨が偽物。
・左右でつり合った。 → 皿に載せていない金貨が偽物。
したがって、天秤ではかる最低の回数は2回です。
推理算[2]誰が嘘つきかな?
太郎君、次郎君、三郎君の3人は、リンゴ、ミカン、バナナのどれかを持っています。3人とも違う果物を持っていて、それぞれが次のように言っています。誰がどの果物を持っているでしょうか。ただし、1人だけ嘘をついているとします。
太郎君「僕はリンゴを持っています」
次郎君「僕はミカンを持っています」
三郎君「僕はリンゴを持っていません」
嘘つき問題を解くコツは、嘘つきを仮定することです。たとえば、太郎君が嘘をついていると仮定します。そうすると、以下のことがわかります。
・太郎君 → ミカンかバナナを持っている。
・次郎君 → ミカンを持っている。
・三郎君 → ミカンかバナナを持っている。
これだとリンゴを持っている人がいなくなります。したがって、「太郎君が嘘をついている」という仮定がまちがっているとわかります。
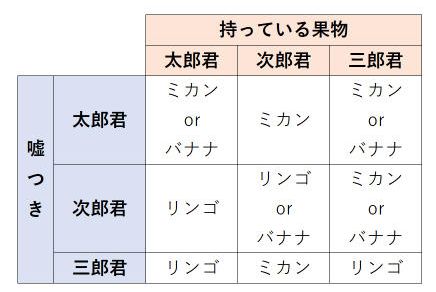
同様に、次郎君と三郎君を嘘つきだと仮定した場合も考えて、以下の表にまとめてみました。
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

