
「百分率、歩合が苦手」を克服する方法
百分率(○%)や歩合(○割)といった表現は日常生活で使用する表現なので、ある程度身近に感じられると思います。一方で、なんとなくわかるので、十分な理解ができていないまま放置されがちな分野でもあります。まずは「比例」の考え方を理解し、その応用をすることで百分率、歩合の考え方を理解していきましょう。
Contents [hide]
基本になるのは「比例の感覚」
割合を理解するためには、まず「比例の感覚」をマスターすることが最優先です。百分率、歩合に入る前に次の2つのチェックポイントを確認しましょう。
チェックポイント[1]比例の表を容易につくれるか
詳細は【「比例が苦手」を克服する方法】を参照ください。次のような問題があったとき、「一瞬で解ける」レベルであるかどうかをチェックします。
AとBが比例の関係にあるとき、下の表の空欄を埋めなさい。
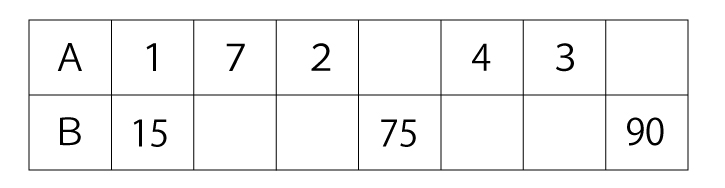
チェックポイント[2]「もとになる数」の意味を理解できるか
「もとになる数」の「もと」は漢字で「元」と書きます。平成元年というと平成1年のことですよね。「もと」は「1」を意味するのです。
つまり「もとになる数」とは「1になる数」を意味するのです。「1にする数」と言い換えた方がわかりやすいかもしれません。
この「もとになる数」の感覚を育てることがとても重要です。比例の表で練習していきましょう。
AとBが比例の関係にあるとき、下の表の空欄を埋めなさい。
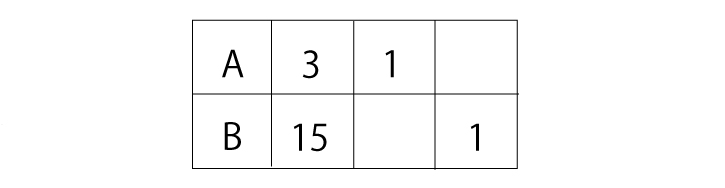
先ほどの【問題1】と違うのは、A=3、B=15という条件が与えられているだけで、AもBも「1」のときの条件が与えられていないことです。A=1のときB=5になるというのは求めやすいかもしれません。
チェックしたいのは「B=1のときA=0.2となるのを直感的に求められるかどうか」です。小数や分数が出てきても、比例の表を直感的に求めることができるかが重要です。
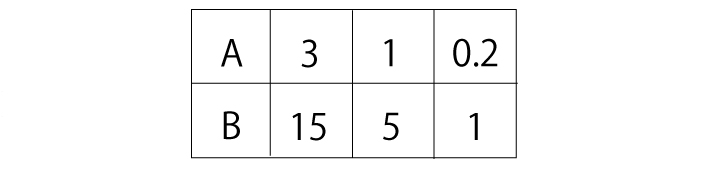
最後に次の問題が解けるかをチェックしてください。
【問題3】
AとBが比例の関係にあります。A=8のときB=20です。
(1)A=1のとき、Bの値を求めなさい。
(2)B=1のとき、Aの値を求めなさい。
【問題2】のときと本質的には同じ問題です。表がなくても求めることができるかをチェックしましょう。
割合の求め方も比例の感覚が大切
「く・も・わ」公式という言葉を聞いたことがあるでしょうか。便利な公式ではありますが、応用力をつけるには公式の丸暗記ではなく、比例の表の感覚をいかして、本質的に理解することが大切です。
「もとにする量」「くらべる量」「割合」
小学生には難しい言葉ですが、「もとにする量」の意味がわかっていれば難しくありません。
【問題4】
(1)クラス40人のうち、15人がサッカーをしています。サッカーをしている人の割合を求めなさい。
(2)クラス30人のうち、野球をしている人の割合は0.3です。野球をしている人は何人ですか。
いずれも文章から「もとにする量」を読み取る必要があります。
(1)(2)いずれもクラス全体の人数を「もとにする量」であることを読み取りましょう。この感覚は読解力にもかかわってくるところです。
この問題では次のような比例の表がかければOKです。

比例の感覚ある子供でも「もとにする量」が何かで勘違いする場合が少なくありません。最初は表を一緒に書いて慣れていく必要があるでしょう。
反復でトレーニング
慣れてきたら反復練習で定着を目指しましょう。このレベルの問題であれば、数字を変えれば簡単に類題を作ることができます。暗記に頼ってしまわないように、英単語用の単語カードを利用し、出題順をランダムにする方法もおすすめです。
百分率、歩合は簡単に求められる
ここでようやく百分率、歩合の話になります。ここまでの内容が理解できていれば、百分率・歩合は平易に理解できるはずです!
百分率、歩合の求め方
割合の「もとにする量」はその数を「1」にすることでした。
百分率では「100」に合わせます。
【問題5】
クラス40人のうち、15人がサッカーをしています。サッカーをしている人は何%か求めなさい。
【問題4】の問題とほぼ同じです。表に「100」を書きましょう。

比例の感覚があれば、「15×\frac{100}{40}=37.5」とできるので、解答は37.5%となりますね。
歩合はもっと簡単です。なぜなら「歩合は割合と同じ」だから。

正確に言うと割合の「読み方」を変えたものが「歩合」です。割合が「0.375」は歩合では「3割7分5厘」と読みます。歩合に苦手意識がある人は、割合を復習するのがよいかもしれません。
日常生活のなかで、百分率と歩合をつかってみる
百分率と割合の変換を求められる問題もあります。「76%を歩合で表しなさい」といった問題です。解答は7割6分ですね。
もちろん「76%=0.76」で「0.76=7割6分」なので、「76%=7割6分」としてもよいです。ただ、「76%=7割6分」と直接求めることができるとよいですが、「76%=7分6厘」のような間違いをしてしまわないか心配です。
そのためには普段から百歩率や歩合に触れておき、「だいたいの量」の感覚を身につけておくことが重要です。スーパーのセールや、野球選手の打率など、百分率や歩合は身の回りに溢れています。
「2割引き」と聞いたら、「半分よりもかなり少ない割引だなー」とか、「4割バッター誕生」であれば、「それでも半分は打てないのか」などのように、「だいたいの量」の感覚が身についていれば間違いは大幅に減らすことができます。普段の生活のなかで、積極的に子供に声掛けをして意識づけをしてあげたい内容です。
百分率、歩合が苦手な子には、比例と割合の根本理解から
百分率、歩合は苦手な子供が多い単元です。理解できないときは、比例や割合の範囲に戻って、根本から理解を見直すようにしてみてください。
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

