数列の公式はどうして成り立つの？ n番目の数や和の求め方を本質から理解しよう

3、5、7、9、11、…という数列の5番目の数11は、3＋2×（5－1）の式で求められます。また、3～11までの和は、（3＋11）×5÷2＝35と計算できます。これらの計算は、有名な数列の公式を利用したものです。

では、そもそもどうして公式が成り立つのでしょうか？ 今回はさまざまな数列の公式について考えてみます。

等差数列のn番目の数とn番目までの和の公式

冒頭で紹介した3、5、7、9、11、…という数列は、3から始まって2ずつ大きくなっていきます。このように一定の数を次々に加えていく数列が等差数列です。

等差数列のn番目の数を求めよう

等差数列のn番目の数は「最初の数＋加える数×（n－1）」で表されます。この公式が成り立つ理由を、3、5、7、9、11、…の数列で具体的に考えてみましょう。

ここまで書き出してみると、3に2を（n－1）個足して求められるのがn番目の数だとわかります。したがって、3、5、7、9、11、…のn番目の数は3＋2×（n－1）です。

等差数列のn番目までの和を求めよう

等差数列のn番目までの和は「（最初の数＋最後の数）×n÷2」です。3＋5＋7＋9＋11＝35は、確かに（3＋11）×5÷2＝35でも求められます。この公式が成り立つ理由は、3＋5＋7＋9＋11と、順番を入れかえた11＋9＋7＋5＋3の和を考えれば理解できます。

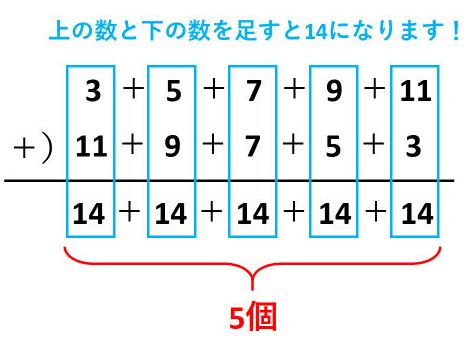
（3＋5＋7＋9＋11）×2＝14×5なので、＝の両側を2で割ります。これが公式の「÷2」の意味です。

等比数列のn番目の数とn番目までの和の公式

2、6、18、54、162、…という数列は、2から始まって3をかけています。このように一定の数を次々にかけていく数列が等比数列です。中学受験ではあまりお目にかからない数列ですが、等差数列と同じように公式を紹介します。

等比数列のn番目の数を求めよう

等比数列のn番目の数は「最初の数×かける数の（n－1）乗」で表されます。□の△乗は、□を△回かけるという意味です。たとえば、3の2乗は3²＝3×3になります。