消去算の解き方は2つ！ 加減法と代入法を理解できれば難しくない

2つ以上のわからない数がある問題で役立つのが「消去算」です。消去算では、式をいくつか作って操作することで、わからない数を求めていきます。今回は、消去算の基本的な解き方を解説します。

足したり引いたりする「加減法」

消去算には2つの解き方があります。1つめは、式を足したり引いたりする「加減法」です。

引き算をしてミカンを消去する

【問題1】で難しいのは、リンゴとミカンの2つの果物について考えなければいけないところです。そのため、リンゴかミカンのどちらかを消してしまいます。「消去算」では、その名の通り、いくつかあるものを「消去」するのがポイントです。

まずはリンゴとミカンの絵を描いて考えます。

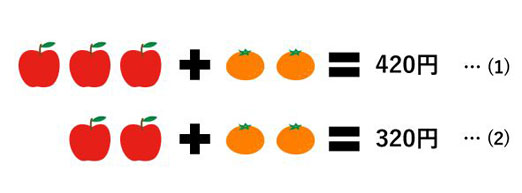
 （1）と（2）のどちらにもミカン2つがあるので、（1）から（2）を引けばミカン2つを消せます。次のように引き算をしてみましょう。

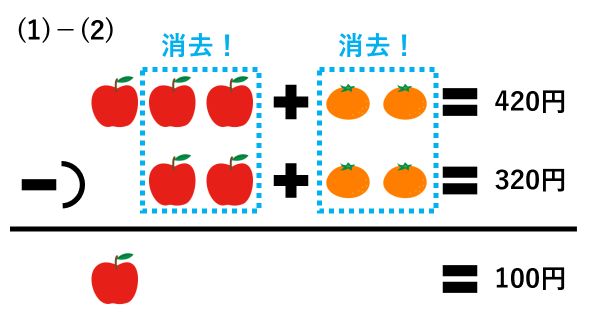
リンゴ1個が100円です。また、（2）から、ミカン2個の値段が320－100×2＝120（円）となり、ミカン1個の値段を120÷2＝60（円）と求められます。

消去算では一般的に、絵を描くのではなく、式を作って計算します。【問題1】では、リンゴを「リ」、ミカンを「ミ」として次の2つの式を作ります。

後は （1）－（2）を計算すれば、リンゴ1個が100円だとわかります。

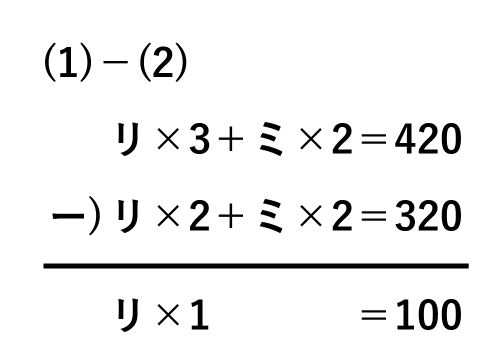
ミカンの個数を最小公倍数にそろえる

【問題1】と同じように、リンゴを「リ」、ミカンを「ミ」として2つの式を作ります。