三角形の面積比を求めよう！ 底辺比と相似比を使えば複雑な問題もスッキリ解決

中学受験算数の図形分野では、三角形が最もよく出題されます。中でも、底辺比や相似比を使って面積比を求める問題は定番です。今回は、面積比を求める問題で役立つ考え方を詳しく解説し、実際に問題を解いていきます。

底辺比と相似比から面積比を求めよう

三角形の面積比問題では、底辺比を使う場合と相似比を使う場合があります。それぞれについて、「なぜそうなるのか？」を理解しましょう。

高さの等しい三角形は「底辺比＝面積比」

高さの等しい三角形では「底辺比＝面積比」が成り立ちます。

中学受験算数で登場する高さの等しい三角形は、多くの場合、次の図のような形をしています。一つの頂点から向かい合う辺に線を引いて三角形を分割しているのが特徴です。

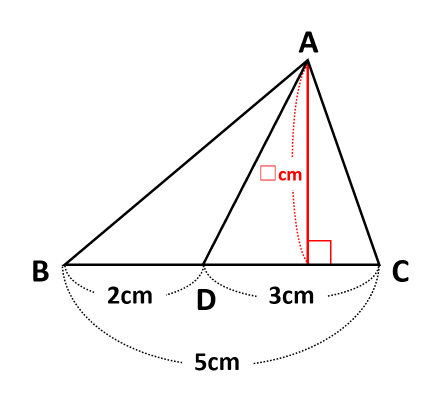
この図では、三角形ABCと三角形ABDと三角形ACDの高さは共通（赤い線）です。この高さを□cmとして、三角形の面積公式「底辺×高さ×\(\frac{1}{2}\)＝面積」に当てはめると、「底辺比＝面積比」の理由がわかります。

したがって、それぞれの三角形の面積について、次の関係が成り立ちます。

これがわかれば、次の図から「三角形ADE＝\(\frac{b}{a}\)×\(\frac{d}{c}\)×三角形ABC」になる理由も理解できるでしょう。

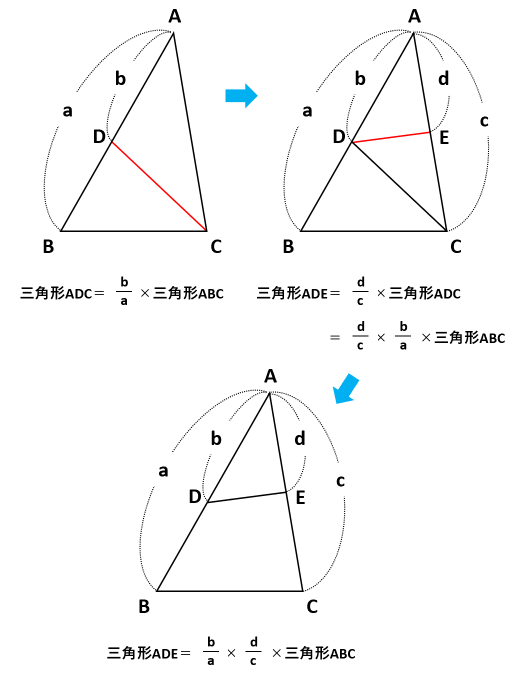
相似な三角形は「相似比×相似比＝面積比」

相似な三角形では「相似比×相似比＝面積比」が成り立ちます。

相似比は、相似な図形において対応する辺の比です。下の図で三角形ABCと三角形ADEが相似ならば、相似比はAB：AD＝AC：AE＝a：bで、\(\frac{d}{c}\)も\(\frac{b}{a}\)になることから「三角形ADE＝\(\frac{b×b}{a×a}\)×三角形ABC」と表せます。したがって、三角形ABCと三角形ADEの相似比がa：bならば、面積比はa×a：b×bです。