円柱や円すいの表面積の求め方。確実に得点するための「3つの手順」も

中学入試の算数では、表面積を求める問題が頻出です。少し難しい分野ではありますが、落ち着いて計算すれば解ける問題も多いので、着実に得点しておきたいところです。

なお、表面積の問題を落としてしまう理由として考えられるのは、計算ミスや、たし忘れ。特に、円柱や円錐（円すい）の表面積を求める問題には円周率の計算が入ってくるので、気を付けないとミスをしてしまう可能性も。そこでこの記事では、表面積を求める問題を得点源にするために心掛けたい3つのステップ、そして円柱や円すいの問題を解くために必要な3つの知識を紹介します。記事の後半では例題をもとに手順を確認していきますので、最後までぜひチェックしてみてください。

表面積の問題を解く「3つのステップ」

円柱や円すいに限らず、表面積を求める問題を解くときは次の3つのステップを意識しましょう。

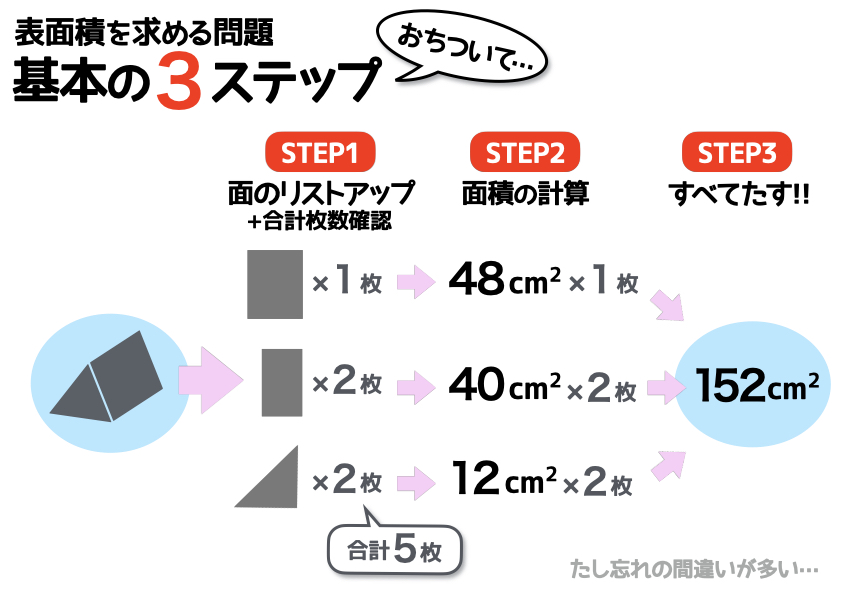
この3ステップを意識することで、計算ミスなどを減らすことができます。なお、ステップ1の「面のリストアップ＋合計枚数の確認」が少しわかりにくいかもしれないので、以下で補足して説明します。

面のリストアップ

中学入試で出題される立体図形は、その多くが複数の面で構成されています。そして当然ながら、表面積を求める問題では、その立体図形を構成する「面」の面積をすべてたす必要があります。つまり特に大切なステップは、計算すべき面をリストアップする（書き出す）ということ。構成する面をリストアップすることで、計算ミスや、たし忘れを防ぐことにもつながります。

ただし立体のままでは、どんな面があるのかちょっとわかりにくいことも。その代表格が、円柱と円すいです。こうした立体図形が問題に出てきた場合には、まずは展開図を書き、そこから構成する面をリストアップしていくのがおすすめです。

合計枚数の確認

表面積を求める問題を解き直してみると、「ひとつの面だけたし忘れていた」という経験はないですか？ これはほとんどの場合、面の「合計枚数」を確認し忘れていたことが原因です。たとえば立方体や直方体だったら、面は6つ。円柱なら3つの面から成り立っています。面のたし忘れは複雑な立体図形であればあるほど発生しやすくなるので、面の合計枚数もしっかりと確認しましょう。

知っておきたい3つの知識 ―― 円柱・円すい

表面積を求める問題のなかでも、苦手な子が多いのが円柱や円すいの問題です。そこでまずは、これらの表面積を求めるために知っておきたい知識を紹介します。

知識1：円柱と円すいを展開させる

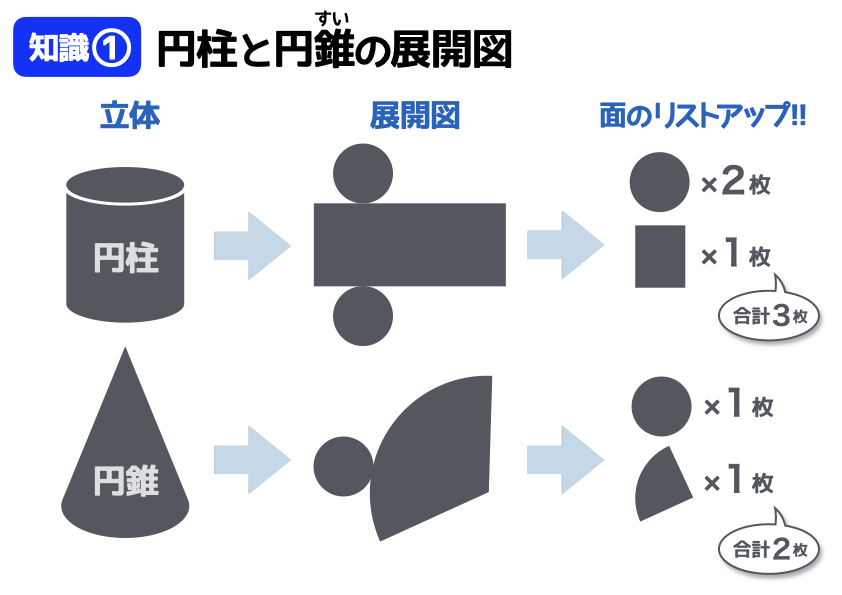
立体のままだと、円柱と円すいはどんな面で構成されているのかわかりづらいですよね。この場合、まずは立体を展開図にしましょう。「円柱と円すいの展開図」と聞くと難しく聞こえるかもしれませんが、それぞれの面はシンプルです。

表面積を求める問題では、上の図の右にあるような「リスト形式」に変換してしまうのがおすすめです。テスト用紙の空きスペースに書き出しておいても良いですね。たとえば円柱を構成する「円」は2枚ですが、1枚分しか計算していなかった、といったミスをしてしまいがち。こうしたミスも、面の枚数をはじめにリストアップしておくことで減らせますよ。

知識2：底面の円周の長さを使う

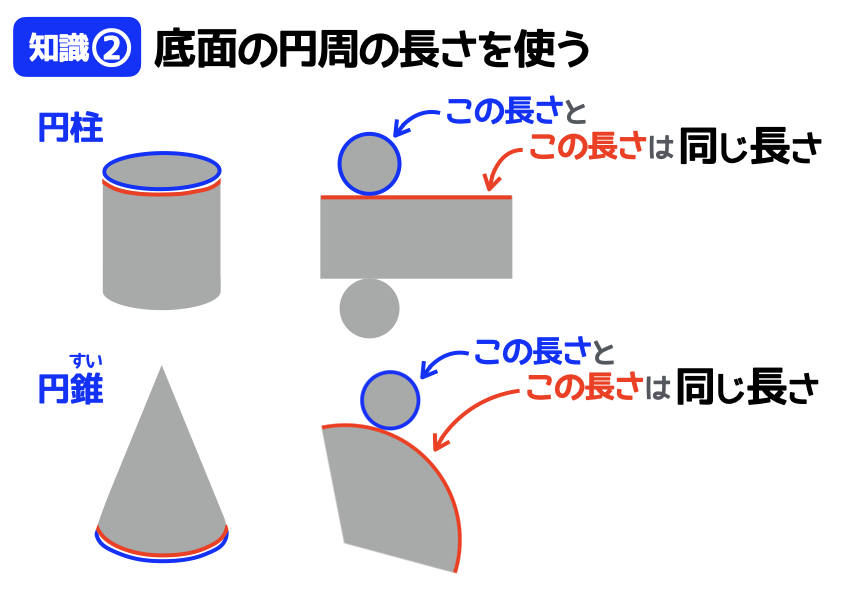
円柱や円すいは、底面が円です。そして表面積の問題を解くうえで、この底面の円周の長さが重要な意味を持ちます。具体的には、円周の長さを求めることで、そのほかの長さがわかるのです。つまり、上の図の赤い線の長さを知りたい場合には、底面の円周の長さを計算すればOK、ということですね。

知識3：円に関連する基本4公式

円や扇形の基本的な公式も覚えておきましょう。面積と円周（弧長）を求める公式ですが、これらは「基本4公式」として押さえておくのがポイントです。

ちなみに解説書のなかには扇形の公式がズラズラと書かれているものもありますが、中学入試においては、まずは次のふたつだけを押さえておけば十分でしょう。

【練習】表面積を求めてみよう

先ほど紹介した「3つのステップ」をもとに、立体図形の表面積を求めていきましょう。

例題1：円柱の表面積

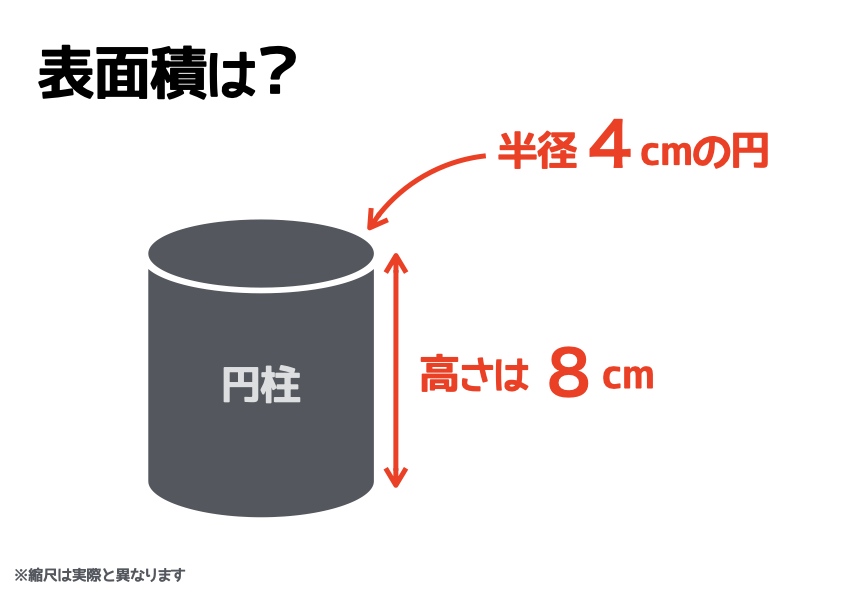
まずは、円柱の表面積を求めていきます。

ステップ［1］面のリストアップ＋合計枚数の確認

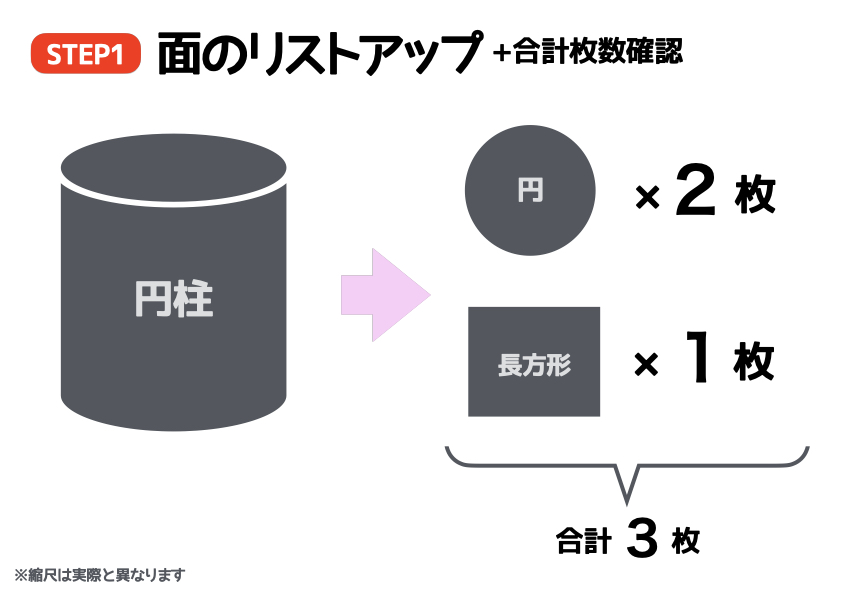
最初のステップは、面のリストアップです。円柱の展開図を想像しながら、面を書き出していきましょう。すると円が2枚、長方形が1枚の、合計「3枚」の面が表れましたね。

ステップ［2］面積の計算

面をリストアップできたら、今度はそれぞれの面積を計算していきます。落ち着いて、ひとつずつ計算していきましょう。

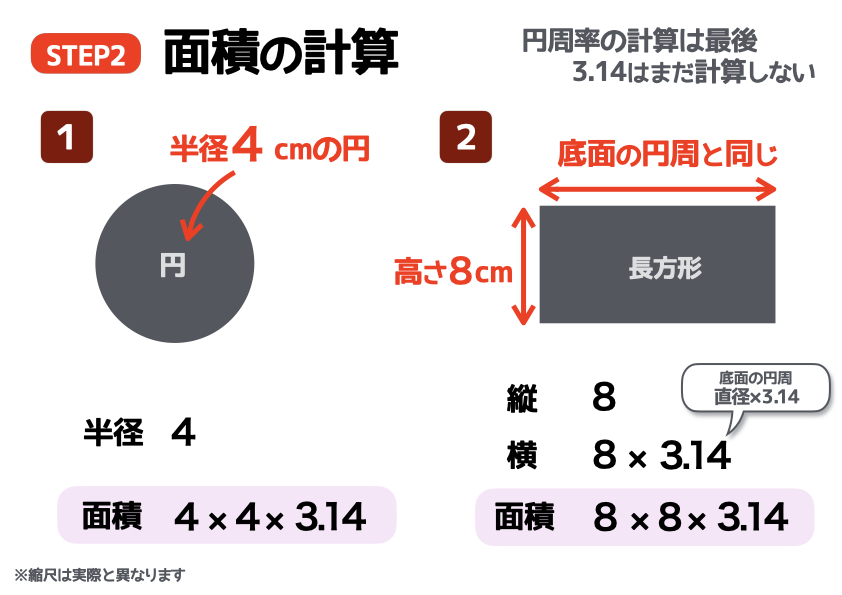
円の面積

円の面積は、比較的簡単に求められます。底面の円の半径が4cmなので、これを面積の公式に当てはめて計算するだけですね。ただし、まだ計算はしません。円周率を含む計算は、最後にまとめて3.14を掛けるのが“鉄則”。なぜなら、計算ミスを減らせるからです

長方形の面積

長方形の縦の長さは、円柱の高さと同じなので8cmです。では、横の長さはいくつでしょうか？ まず横の長さは、円柱の「底面の円周」と同じでしたよね。底面の円の半径が4cmなので、円周の長さは8cm（直径）×3.14cmです。つまり、長方形の横の長さも8cm×3.14cmということです。

縦と横の長さがわかったので、長方形の面積も求められます。

長方形の面積＝8×8×3.14（㎠）

ステップ［3］すべてたす

最後に、リストアップした面の面積をすべてたします。

円が2枚、長方形が1枚の合計3枚の面積を、落ち着いてたしていきましょう。このとき円周率の計算を最後にすることで、小数点を含む掛け算の計算は1回だけですみます。

答えは、301.44㎠です。

例題2：円すいの表面積

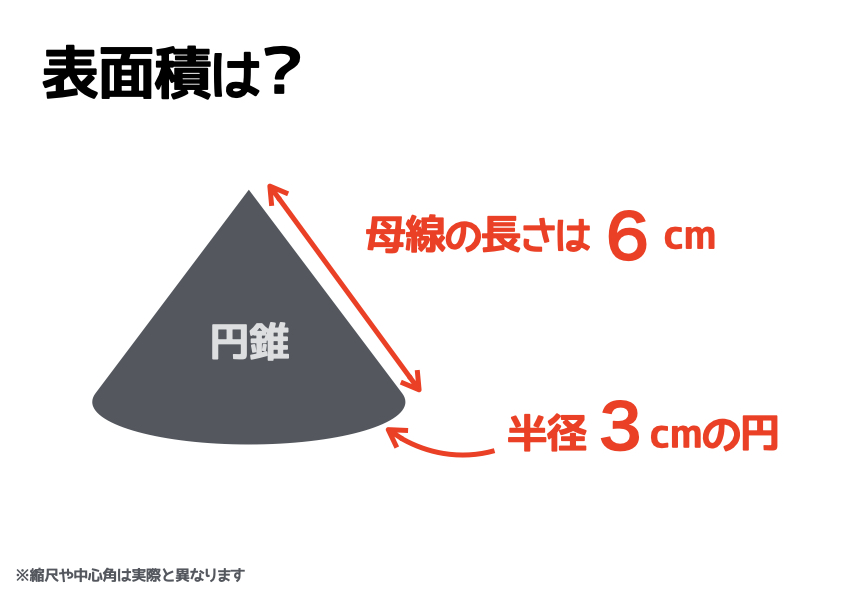
次に、円すいの表面積を求めていきましょう。

ステップ［1］面のリストアップ＋合計枚数の確認

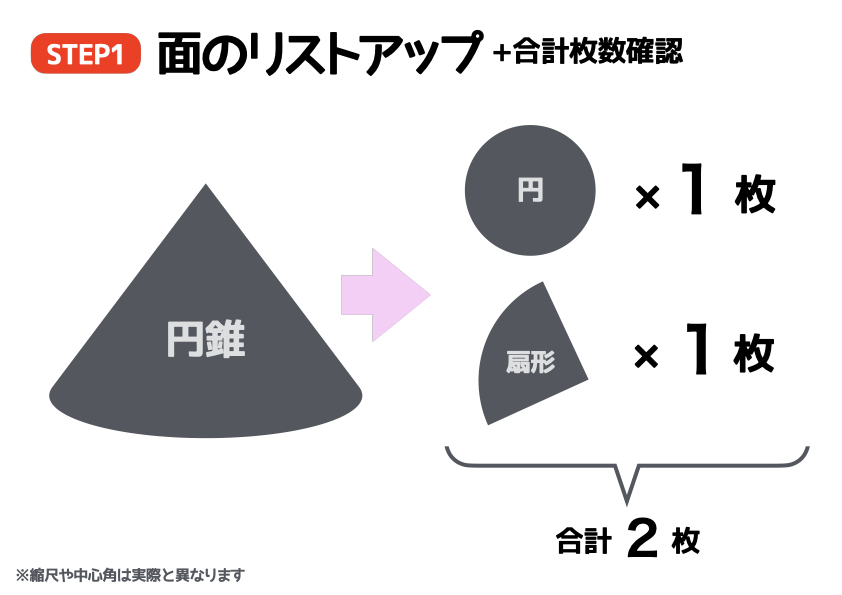
最初のステップは、面のリストアップです。円すいの展開図を想像しながら、面を書き出していきましょう。円すいは、底面の円が1枚、そして扇形が1枚の、合計「2枚」ですね。テストのときは、面の形と枚数をテスト用紙に書き出しておくことがコツです。

ステップ［2］面積の計算

次は面積の計算ですが、扇形の面積を求めるのはちょっと手間が掛かります。まずは落ち着いて、必要な情報を整理しましょう。

円の面積

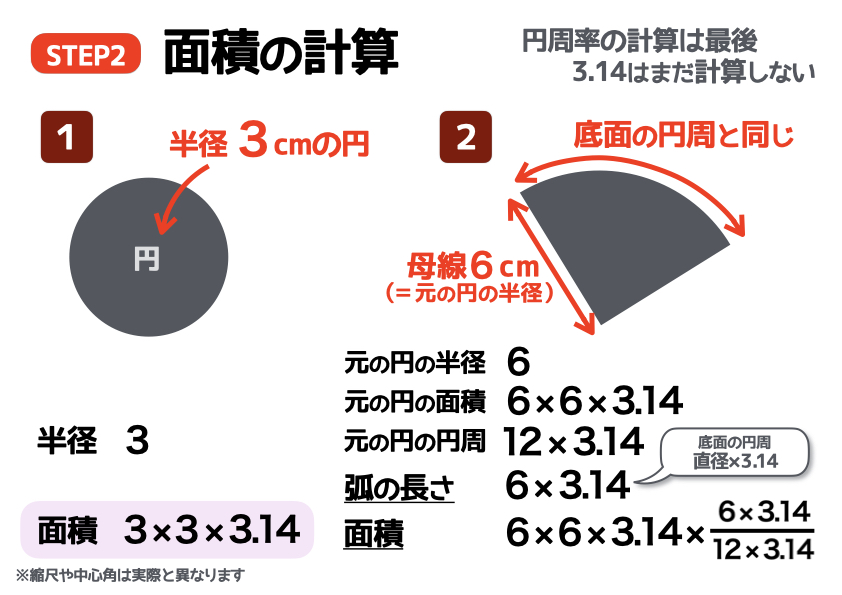
底面の円の半径が3cmとわかっているので、面積の公式に当てはめればOKです。ただし「円柱」の計算と同じく、円周率の計算は最後にまとめておこなうので、まだ計算はしません。

扇形の面積

扇形の面積や弧長を計算するときに、はじめに考えておきたいことがあります。それは、“元になる円”を想像することです。つまり扇形を「円の一部」として捉えてみるのですね。

元になる円の半径は、母線と同じ長さのため6cmです。半径さえわかれば、元になる円の面積や円周を計算できます。

では、この扇形の孤の長さはいくつでしょうか？ 孤の長さは、底面の円周と同じ長さでしたよね。そのため、底面の円の円周を計算することで弧の長さがわかります。孤の長さがわかれば、面積も計算できます。このとき、「扇形の元になる円」と「円すいの底面の円」を混同しないように気をつけましょう。

そして扇形の面積は、元になる円の面積に「割合」を掛けることで導き出せます。この問題の場合には、弧の長さから割合を求めましょう。このとき、分母は「元になる円の円周」、分子は「扇形の弧の長さ」で割合を求められますよ。

ステップ［3］すべてたす

最後は、これまで計算してきた面積をたしていきます。このとき円周率の計算は最後にすることで、小数点の掛け算は1回ですみますよ。

答えは、84.78㎠です。

【補足】円すいの扇形の面積

扇形の公式は、まずは“元になる円”を想像して、その扇形がどのくらいの割合を占めるのか、を考えるのがおすすめとお伝えしました。しかし実は、円すいの側面を構成する扇形の面積だけは、もっと簡単に求めることができます。

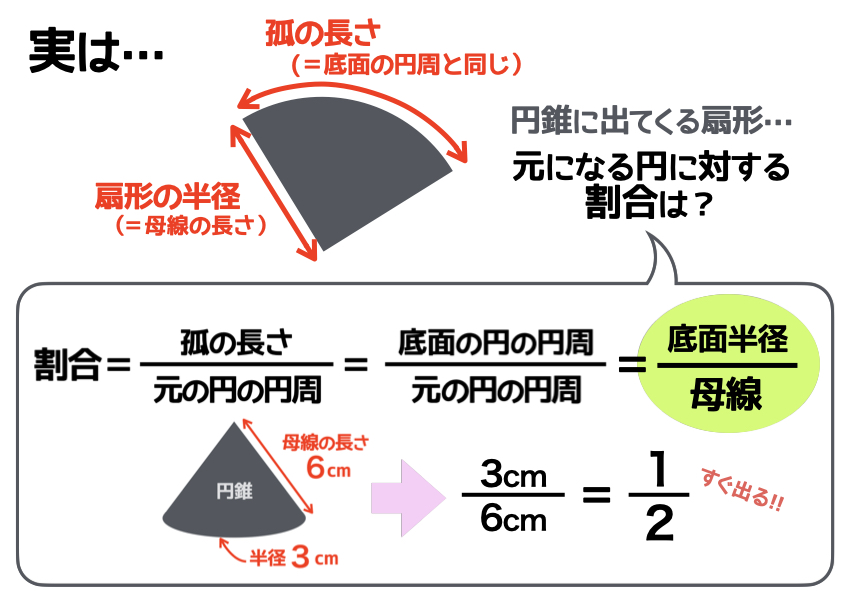
元になる円のどれくらいの割合を扇形が占めるか計算しようとすると、上の図のように、「分子＝底面積の半径」「分母＝母線」という分数になることがわかります。たとえば先ほど解いた「例題2」では、母線の長さが6cm、底面の半径は3cmでした。すると側面の扇形は、元になる円の「2分の1」ということがすぐにわかるのですね。

まとめ

円柱や円すいの表面積について、計算のコツを交えつつ解説しました。表面積を求める問題を間違ってしまうのは、多くの場合「計算ミス」や「たし忘れ」が原因です。お伝えした以下のステップを改めて振り返りつつ、落ち着いて計算しながら、表面積の問題を得意にしていきましょう！

※記事の内容は執筆時点のものです