
基本から応用まで使える! 割合の問題を解くときに役立つ「線分図」の考え方
算数の「割合」は小学校5年生で学習します。私達大人は普段の生活で割合の概念に触れる機会が多いですが、小学生は割合に触れることがあまりなく、算数のなかでもつまずく子が多い単元です。
とはいえ、学校で割合の復習に多くの時間を割いてはくれません。実際に筆者が塾講師や家庭教師で算数を教えていたときにも、割合を苦手とする子がたくさんいました。
そのため、もし子供が割合でつまずいていたら、家庭で勉強をフォローする必要があります。そこで、今回は家庭で割合を勉強するときに役に立つ「線分図」を使った考え方を解説します。
Contents [hide]
割合とは
割合とは全体に対して占める分量のことです。小学校ではこれを次のような公式で習います。
割合=比べられる量÷もとにする量
このように、公式を習いますが、私が子供たちに算数を教えるなかで気が付いたのは、そもそも「比べられる量」と「もとにする量」この言葉で戸惑う子が多いということです。
例えば次のような問題があります。
■問題
5年生は全員で100人いて、そのうち女子は40人です。女子の割合を求めなさい。
これを先ほどの公式にあてはめると「割合=40÷100」になり、答えは0.4(4割)と導き出せるのですが、「比べられる量」が40なのか100なのかと戸惑う子が結構います。
また「小さい数÷大きい数で解く」といったように、公式に機械的に数をあてはめて、とにかく答えを出そうとする子もいます。
割合をイメージできていなかったり、公式に数をあてはめるだけになったりするのです。
こうなってしまうと、少し難しい問題になったとたんに対応できなくなってしまいます。
そこで割合を理解して解くために使えるのが、線分図を書いて割合を視覚的にとらえる方法です。
割合を線分図に表して解く
割合を線分図に表して解く方法はシンプルです。先ほどの問題を例に線分図を書いてみます。
■問題
5年生は全員で100人いて、そのうち女子は40人です。女子の割合を求めなさい。
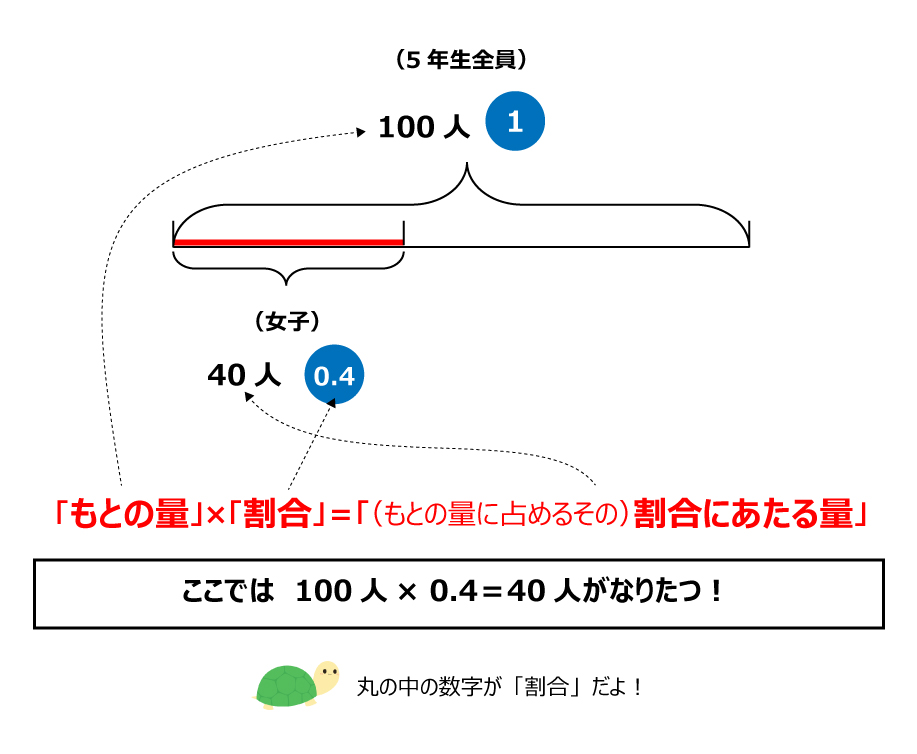
上の図のように、わかっている数と線を書き込んで割合をとらえます。ここで重要なのは、「もとの量」×「割合」で「(もとの量に占めるその)割合にあたる量」(=比べられる量)が求められることです。
割合の基本的な問題を線分図で解いてみる
実際の問題で具体的な解き方をいくつかみていきましょう。学校で学習する割合の基本的な問題のパターンは大きく次の3つです。
[1]「割合」を求める問題
[2]「割合にあたる量」を求める問題
[3]「割合」と「割合にあたる量」から「もとの量」を求める問題
それぞれの問題を線分図に表わして解いてみます。
[1]「割合」を求める問題
■問題
5年生は全員で100人いて、そのうち女子は40人です。女子の割合を求めなさい。
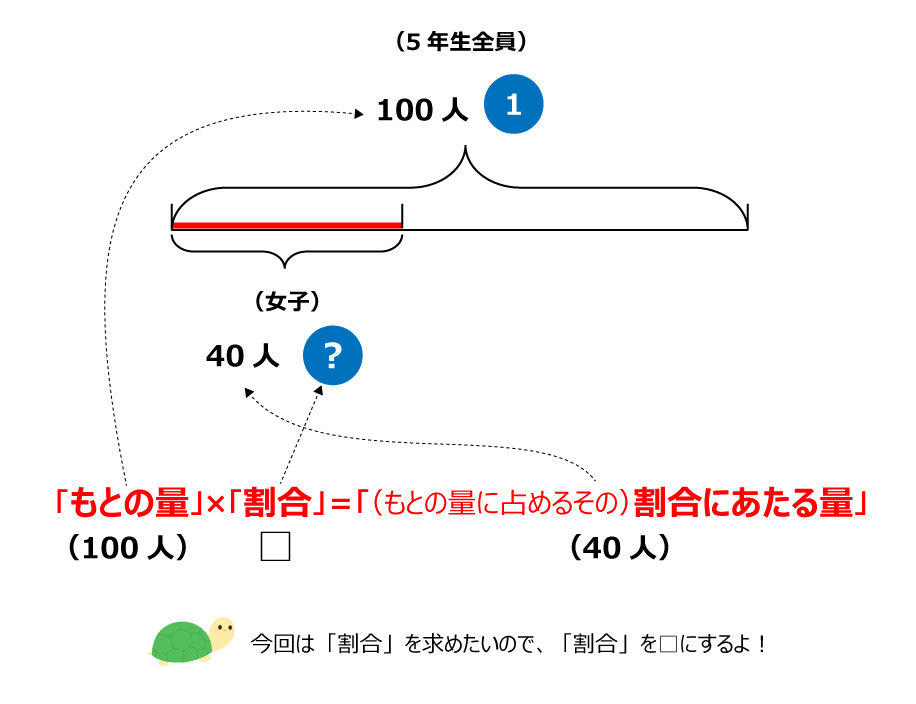
(線分図にわかっている数を書き込む)
「もとの数」×「割合」=「割合にあたる量」
なので、ここでは
100人×□=40人となる
100人×□=40人より
□=40÷100
□=0.4
答えは0.4となる
[2]「割合にあたる量」を求める問題
■問題
5年生は全員で100人いて、そのうち女子は4割です。女子の人数を求めなさい。
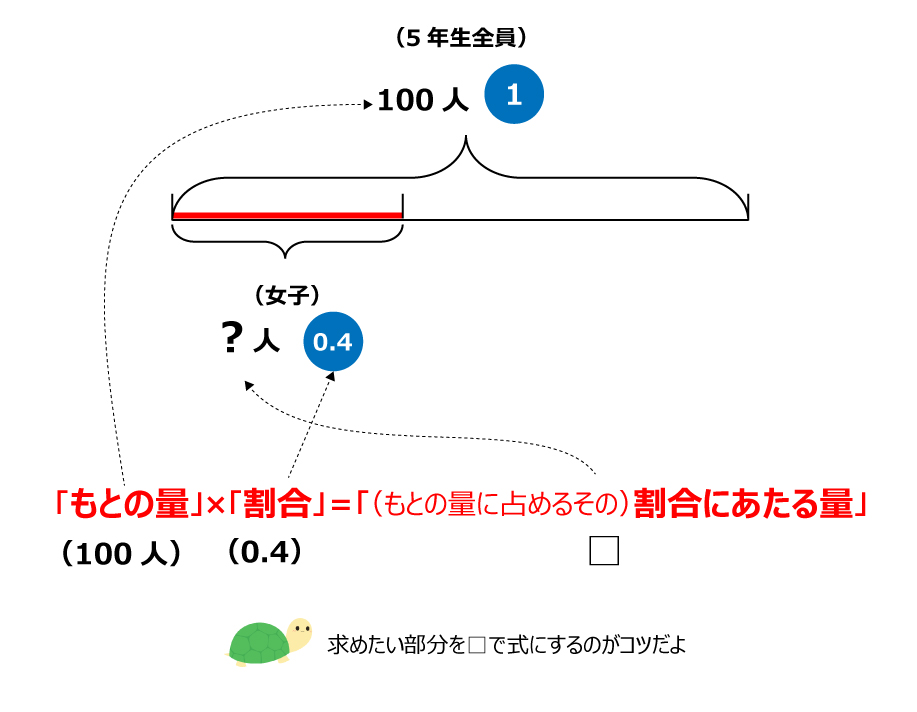
(線分図にわかっている数を書き込む)
「もとの数」×「割合」=「割合にあたる量」
なので、ここでは
100人×0.4(4割)=□という式になる
100人×0.4=40人
答えは40人となる
[3]「割合」と「割合にあたる量」から「もとの量」を求める問題
■問題
5年生の女子は40人で、5年生全員の4割にあたります。5年生は全員で何人でしょうか。
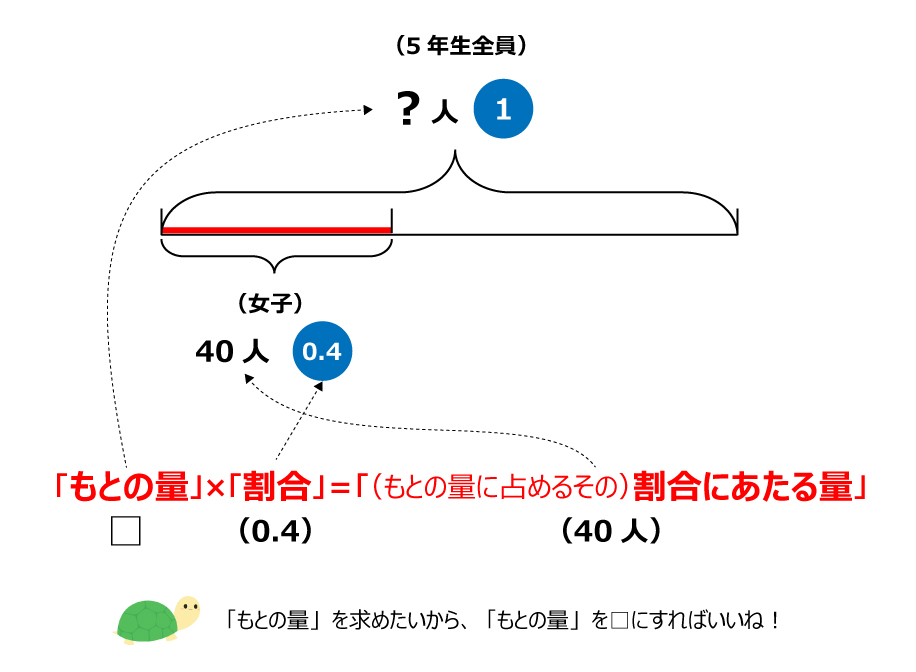
(線分図にわかっている数を書き込む)
「もとの数」×「割合」=「割合にあたる量」
なので、ここでは
□×0.4=40人となる
□×0.4=40人より
□=40÷0.4
□=100人
答えは100人となる
このように、線分図にわかっている数を書き込むことで、割合が全体に占める分量のことだと感覚的に理解できます。また、公式にただ数字をあてはめるだけでなく、問題を解くこともできます。
割合が「1」より大きい場合
「2割増し」や「3割増し」のように、割合が「1」より大きくなる場合もこの線分図を使うと理解しやすくなります。
■問題
今年の5年生は120人で、去年より2割増えました。去年の5年生は何人だったでしょうか。
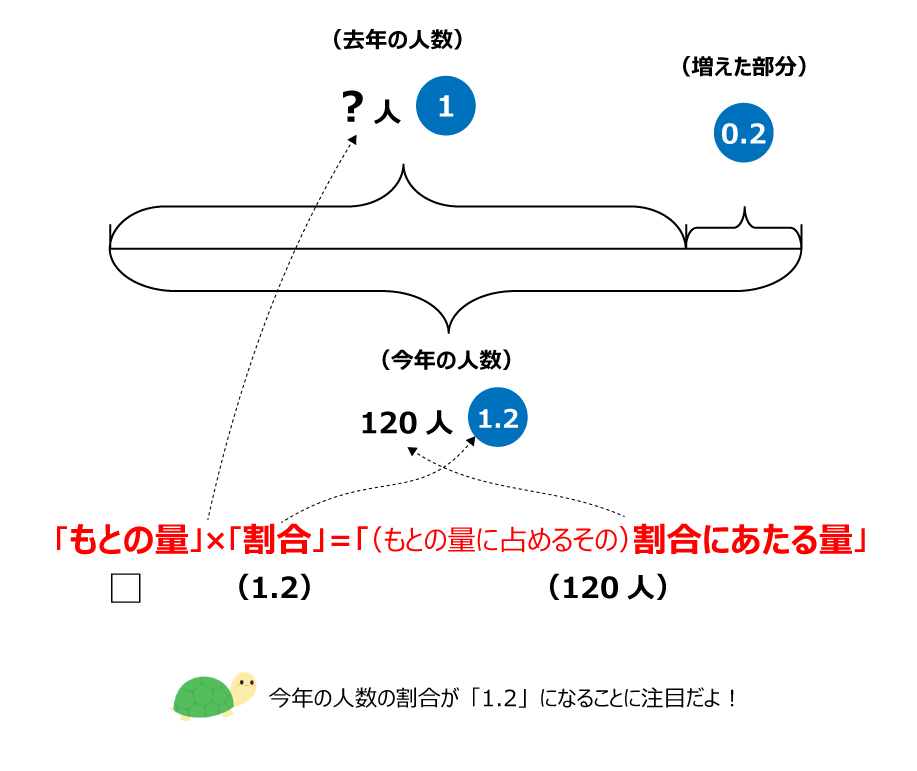
(線分図にわかっている数を書き込む)
「もとの数」×「割合」=「割合にあたる量」なので、
□×1.2=120人となる
□×1.2=120人より
□=120÷1.2
□=100人
答えは100人となる
このように、「もとの量」の割合を「1」とし、昨年よりも増えているため割合が「1.2」とすることがポイントです。
[応用]中学受験 算数の「売買損益」にも使える! 線分図を使った割合の解き方
線分図を使って割合の問題を解く方法は、中学受験 算数の単元でもある「売買損益」にも役立ちます。次のような売買損益の問題を線分図を使って解いてみましょう。
■問題
原価500円の品物に3割の利益を見込んで定価をつけました。定価はいくらでしょう。
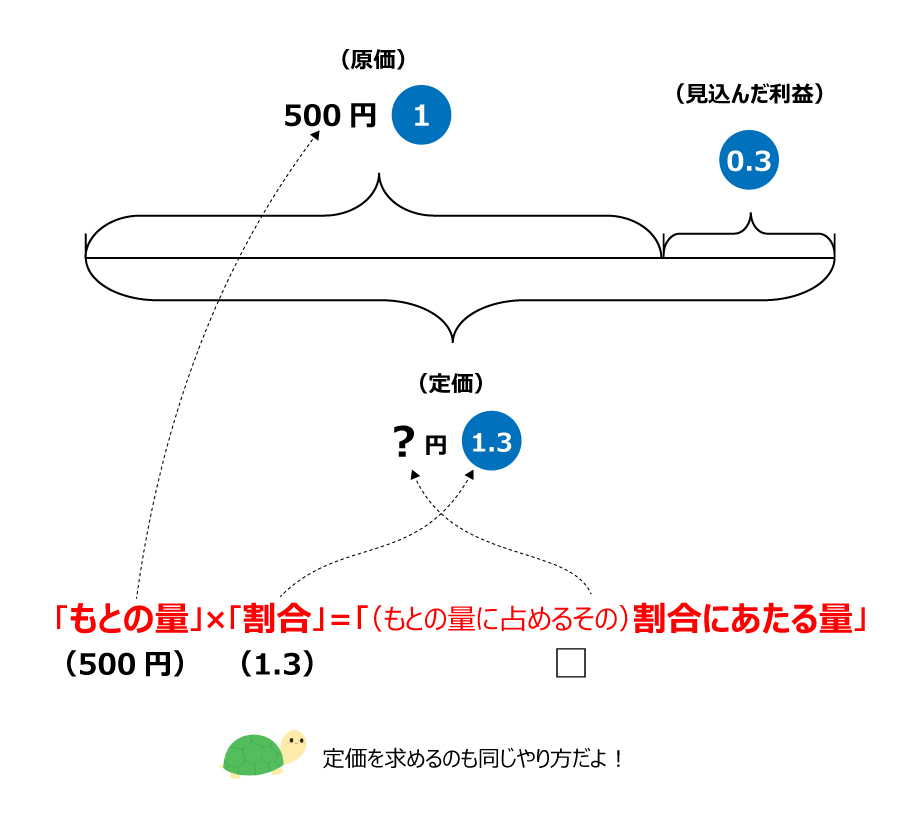
(線分図にわかっている数を書き込む)
「もとの数」×「割合」=「割合にあたる量」
なので、ここでは
500×1.3=650となり、
答えは650円となる
■問題
原価500円の品物に3割の利益を見込んで定価をつけましたが売れませんでした。そこで4割引にして売りました。その場合の損益はいくらでしょうか。

上の線分図より
500×1.3=650となり、
定価は650円ということがわかる
下の線分図から
650×0.6=390円となり、
売り値は390円ということがわかる
損益部分は2つの線分図から
500円-390円=110円
110円の損だということがわかる
このように線分図を書く練習をしておくと、応用問題や中学受験 算数の問題を解く際にも役に立ちます。
お子さんが割合をイメージできていない場合まず、学校でならう割合の問題を線分図に表す練習から始めるのがおすすめです。最初は「なぜわざわざ線分図に?」と思うかもしれませんが、慣れればとても使えるツールになります。是非ご家庭で取り組んでみてください。
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

