
小学生でもスッキリ理解できる! 体積比のコツと求め方
図形問題がとにかく苦手。立体図形を見ただけで尻込みしてしまう。
体積比を使った問題は解説を読んでも理解できない。
このような悩みを抱えた中学受験生は多いようです。「体積比」の理解が進まない理由は、大きく分けると次のふたつに集約されます。
■体積比の理解が進まない理由
・体積比が2種類に分けられることを知らない
・体積を公式でとらえている
ひとつでも当てはまれば、これからお話する内容は役立つはずです。体積比の理解が、グンと進む可能性があります。
Contents [hide]
体積比の求め方
そもそも体積比とは、その名のとおり「体積の比」のことです。体積が5㎤の立体と3㎤の立体の体積比は、5:3ですね。このようにそれぞれの立体の体積がわかっている場合には、簡単に体積比を求められます。では、体積がわからない場合はどうでしょうか? 実は体積がわからなくても、次の条件を満たせば体積比を求められるのです。
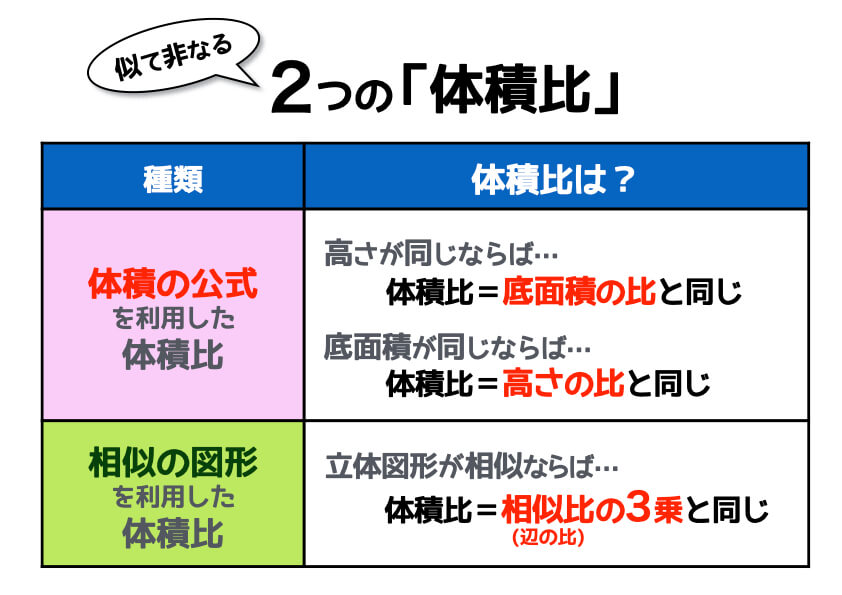
[1] 体積の公式を利用
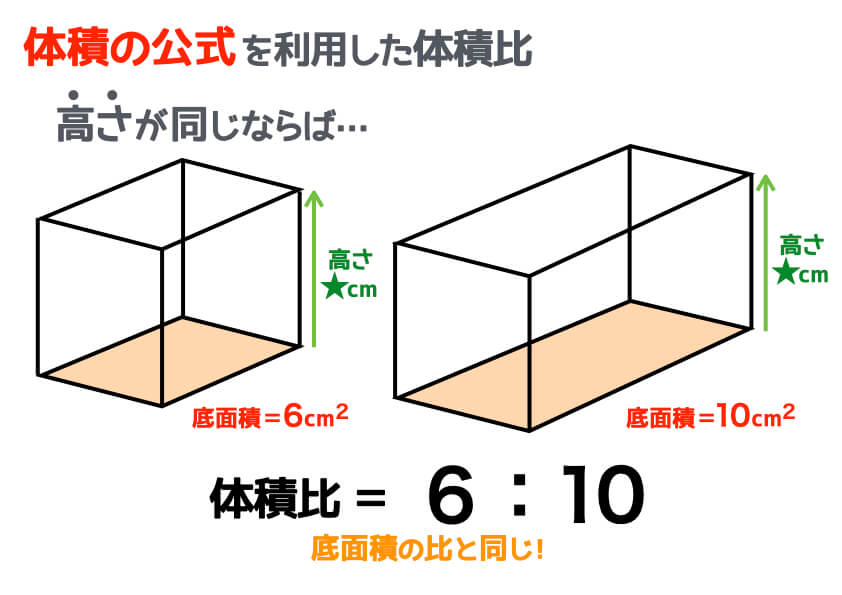
高さが同じふたつの立体があるとします。この場合、体積比は「底面積の比」と等しくなります。次のような直方体であれば、体積比は6:10です。簡単に表現すると3:5ですね。直方体の体積の公式は「底面積×高さ」のため、高さが同じであれば、体積は底面積に比例します。
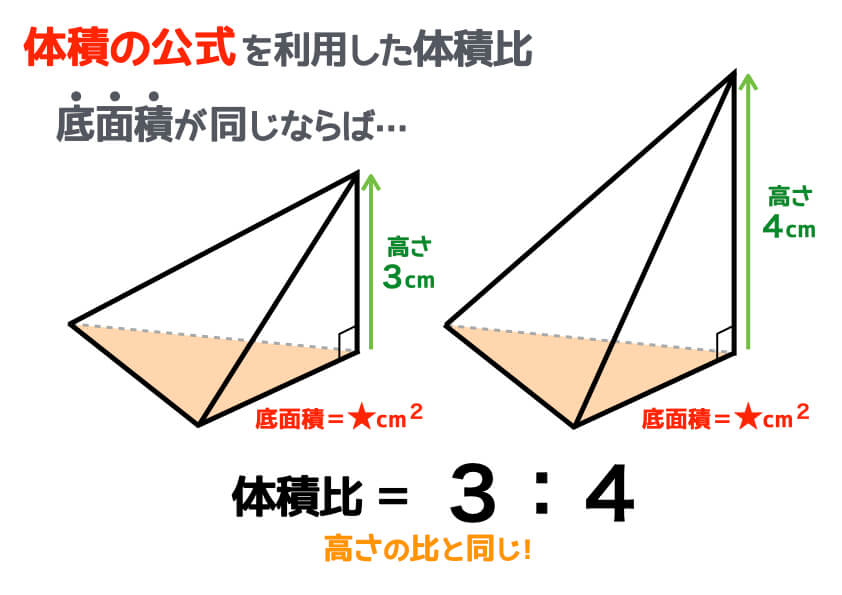
次に、底面積が同じふたつの立体があるとします。この場合、体積比は「高さの比」と等しくなります。次のような三角すいであれば、体積比は3:4です。三角すいの体積の公式は「底面積×高さ÷3」なので、底面積が同じであれば体積は高さに比例します。
[2] 相似の図形を利用
ふたつの図形が相似な場合にも、体積比を求めることができます。この場合、体積比は「相似比(辺の長さの比)の3乗」と等しくなります。
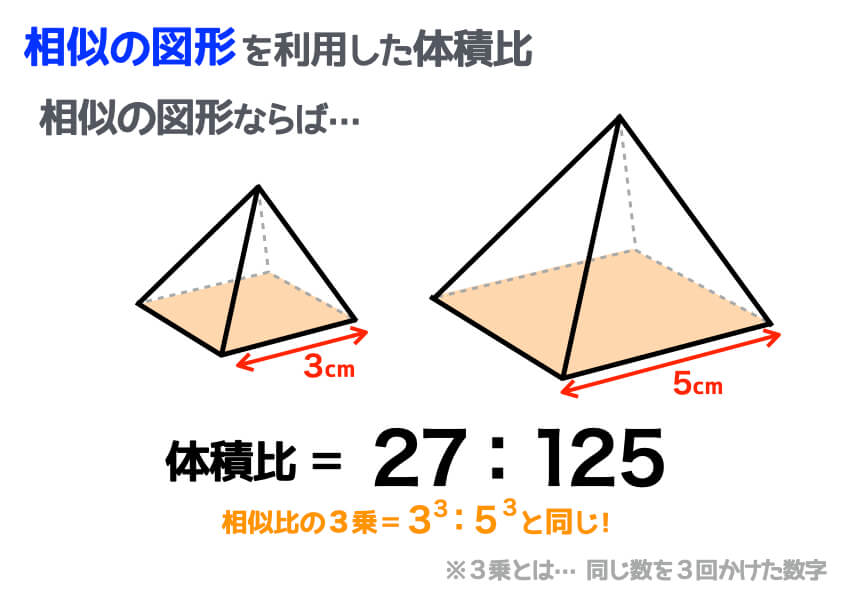
相似とは、形は変わらず、大きさだけが異なる図形同士を指す言葉です。上の図形であれば、どの辺の長さを測っても比は3:5です。先ほどお伝えしたとおり、体積比は「相似比の3乗」と等しくなるため、体積比は27:125となります。
体積比を理解するコツ
体積比を正しく理解するためのコツを紹介します。体積比だけでなく、立体図形の問題に取り組むときにも役立つので、ぜひマスターしましょう!
体積比のコツ
1.体積をイメージでつかむ
2.線、平面、立体の関係をおさえる
[コツ1]体積をイメージでつかむ
「体積を求めなさい」という問題に出会ったとき、「体積の公式」を記憶のなかから引っぱり出していませんか? 公式を思い出すのもたしかに大切ですが、実は「底面がどこか」という視点で立体図形を眺めると体積の問題は解きやすくなります。イメージとしては、“底面積に色を塗る”感覚です。
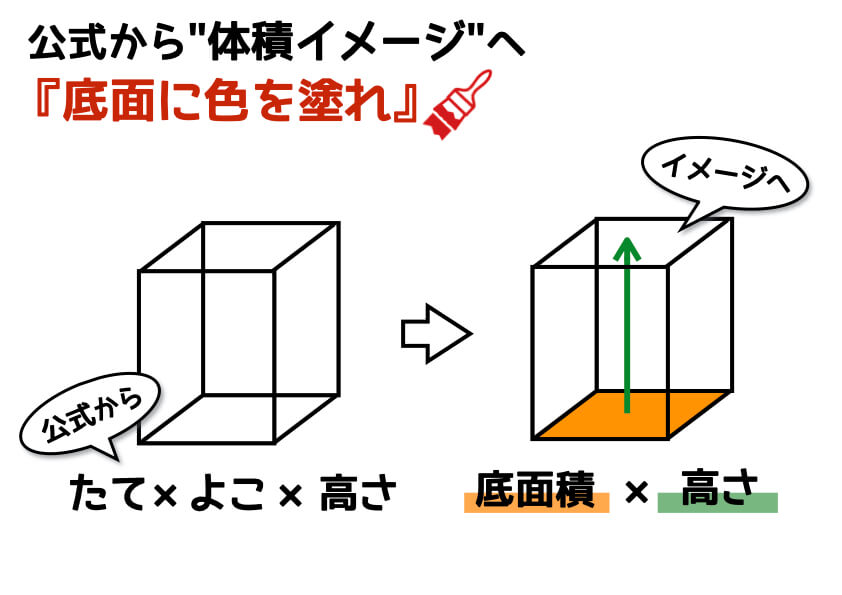
立方体や直方体だけでなく、円柱や円すいなども底面積に色を塗る感覚で見てみると体積のイメージがふくらみますよ。
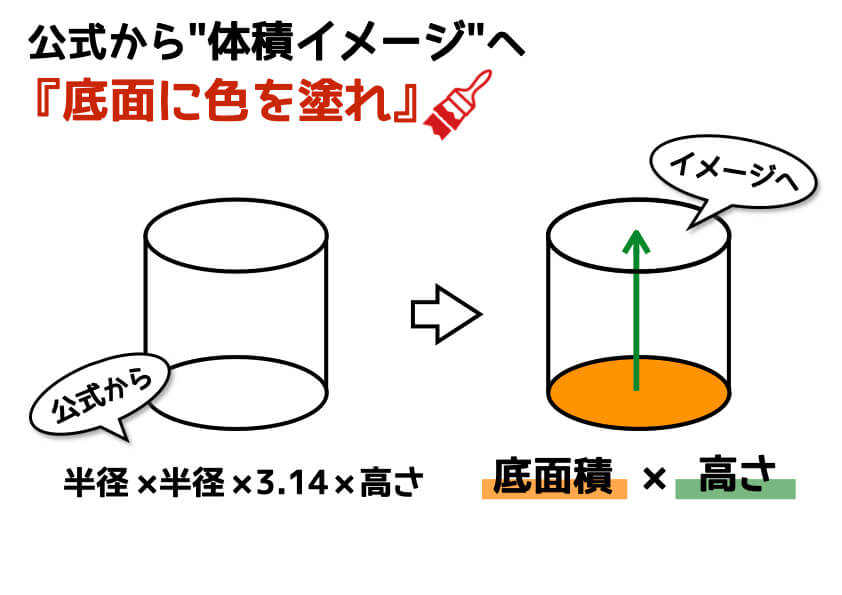
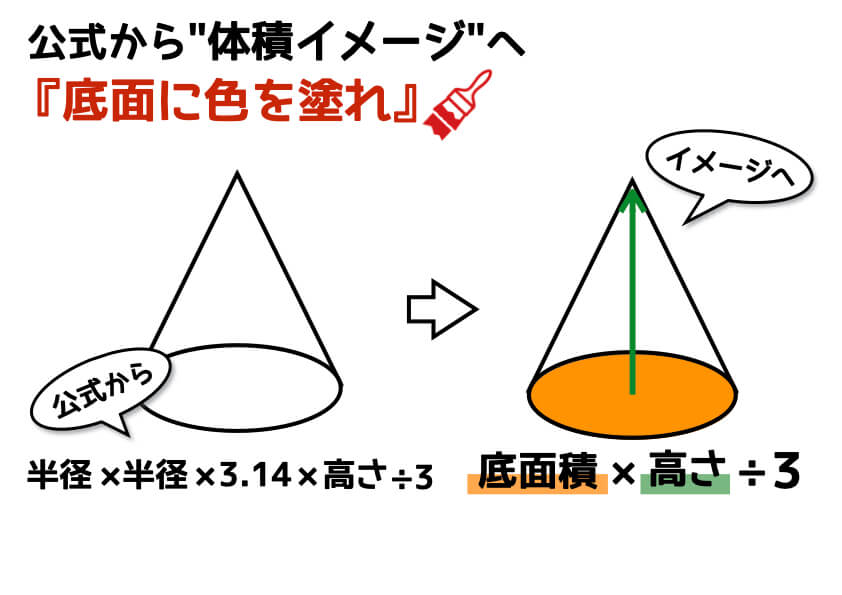
[コツ2]線、平面、立体の関係をおさえる
体積を正しく理解するためには、線、平面、そして立体の関係を改めて理解しておくことも大切です。
下の図のように、1本の「線」があるとします。この線を平行移動すると「平面」になり、その平面をさらに平行移動すると「立体」になります。
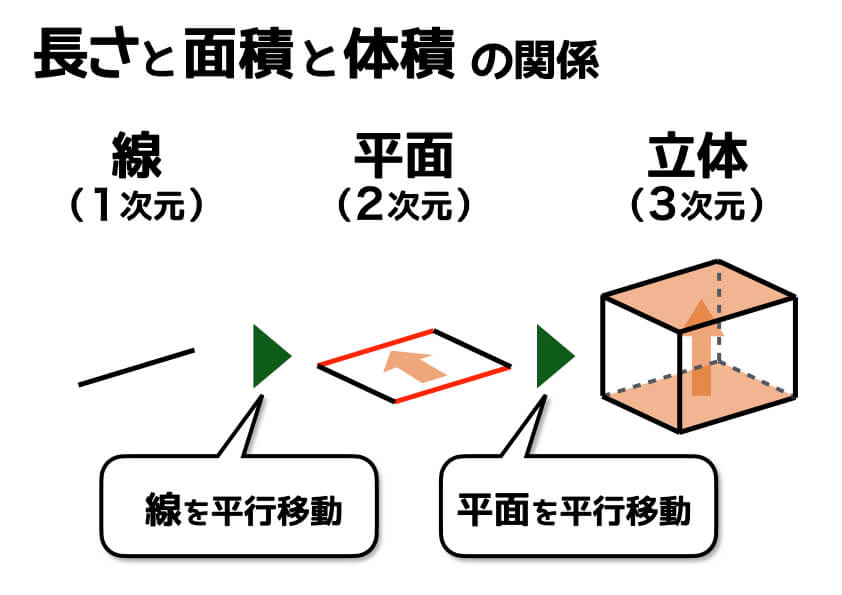
では、線と平面、そして立体の“大きさ”を表すにはどうすれば良いでしょうか? まず、線の大きさを表すのは「長さ」です。メートルやインチなど単位はさまざまですが、どれも「長さ」の単位ですね。次に、平面の大きさを表すのが「面積」。面積は、「長さ」と「長さ」を掛け合わせたものです。そして立体の大きさを表すのが「体積」です。体積は、「長さ」と「長さ」と「長さ」を掛け合わせたものと言うことができます。
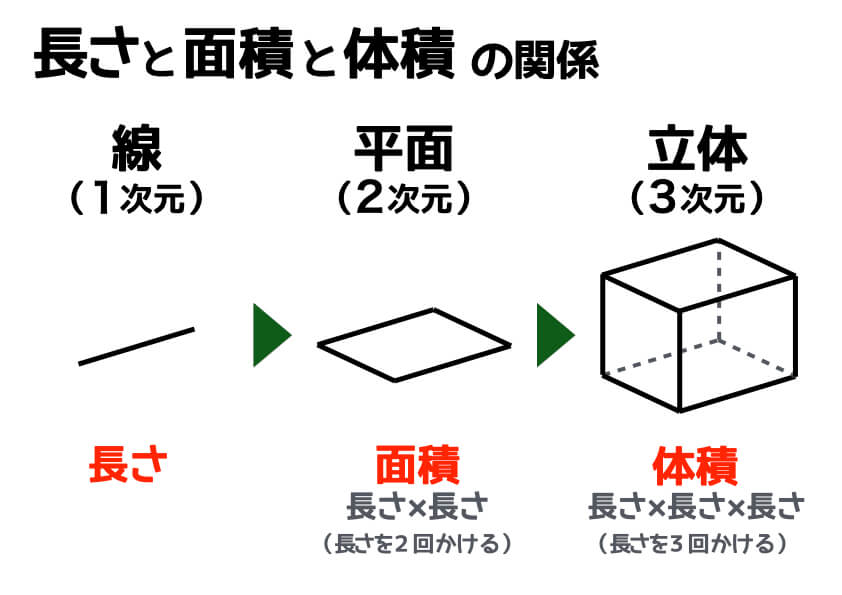
長さが2倍になったとすると、面積は「タテ」も「ヨコ」も長さが2倍になるため4倍(2×2)となります。一方で、体積は「高さ」も2倍になるので8倍(2×2×2)となるのです。
体積比の例題
体積比の例題をふたつ紹介します。
例題1 ―― 四角すいを切断
長方形ABCDを底面とする四角すいP-ABCDがあります。辺BCを3:2に分ける点をQ、辺ADを3:2で分ける点をRとします。この四角すいをP,R,Qを通るように切断したときにできるふたつの立体の体積比を、最も簡単な整数で表しなさい。
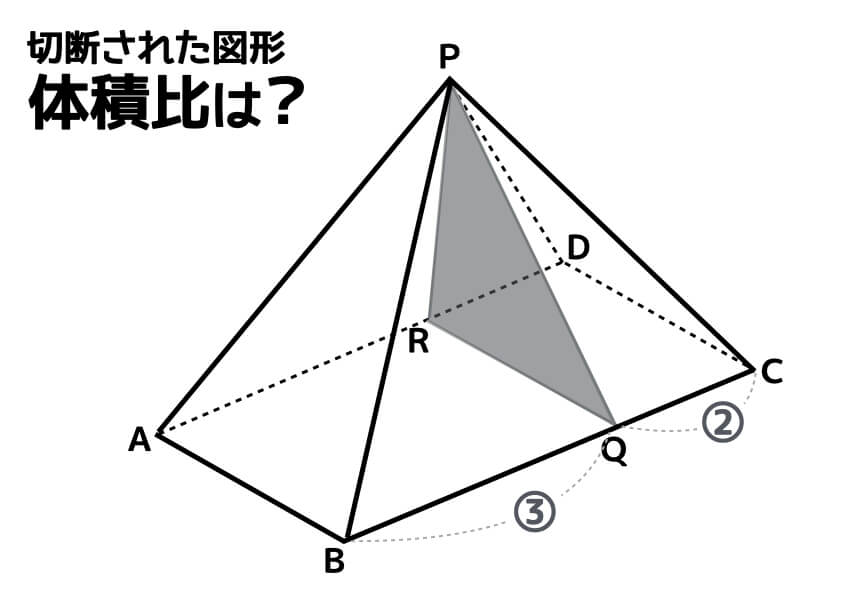
まずは、「どこが底面か」を意識しながらふたつの立体を眺めてみましょう。それぞれの立体の底面を、下の図のようにイメージできましたか?
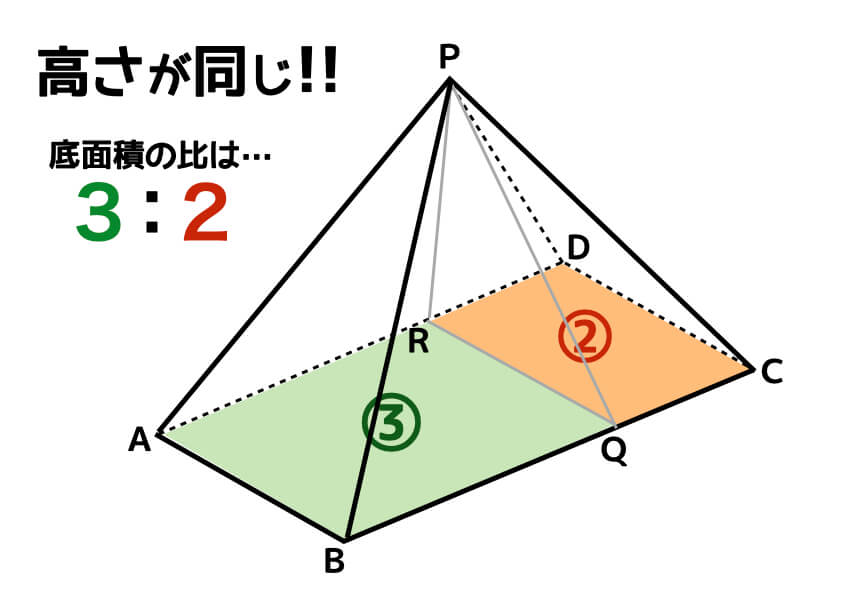
底面に色を塗るイメージがつかめると、切断されて生まれた立体は、高さが同じふたつの四角すいであることがわかりますね。それぞれの底面積の比は3:2のため、体積比も同じ比となります。つまり答えは「3:2」です。
例題2 ―― 三角すいを切断
三角すいP-ABCがあります。辺PAを2:1に分ける点をXとし、点Xを通り、面ABCと平行になるように図形を切断した。このとき、切断する前の立体P-ABCと、切断された立体P-XYZの体積比を最も簡単な整数で表しなさい。
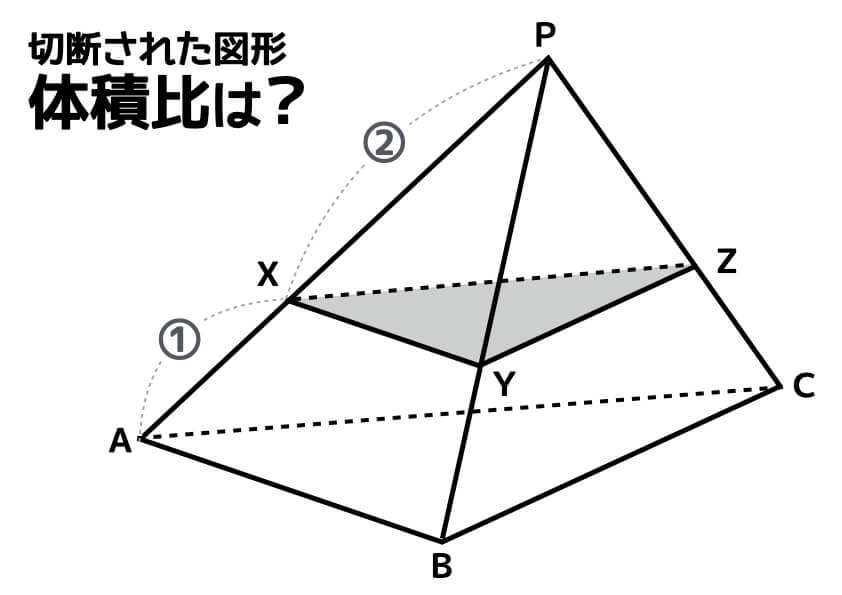
例題1と同じく、まずは「どこが底面か」を意識しながら立体を眺めてみましょう。下の図のようにイメージできましたか?
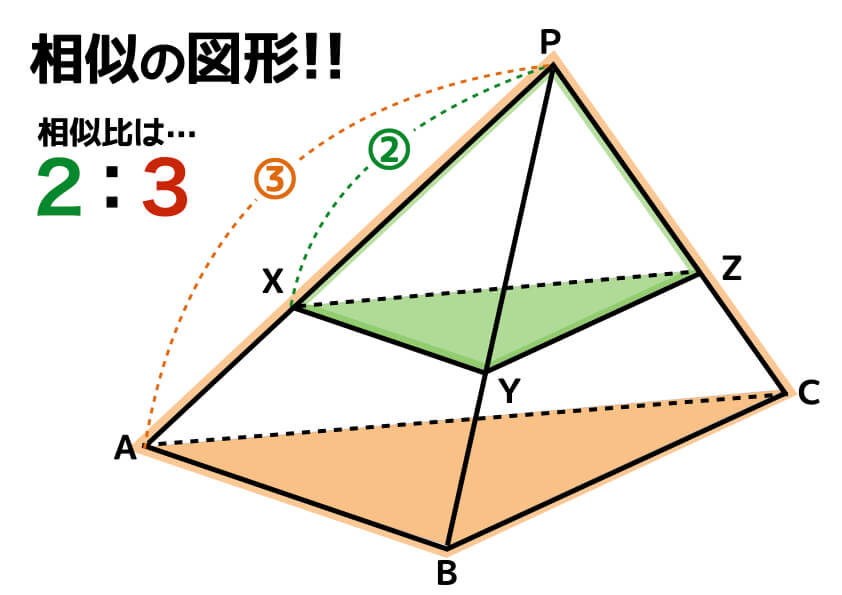
ふたつの立体は相似なので、体積比は「相似比の3乗」と等しくなります。相似比は2:3とわかるので、あとは計算です。
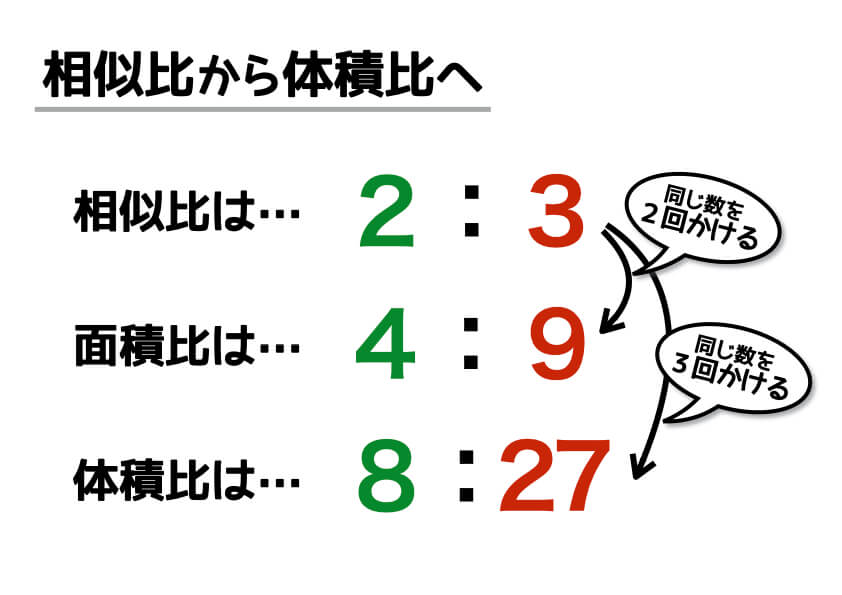
相似比を3乗すると、体積比は8:27。つまり答えは「8:27」です。
まとめ
立体図形に対し、苦手意識を持つ子は少なくありません。特に体積比の理解が進まない子は多く、その理由は次のふたつに集約されます。
■体積比の理解が進まない理由
・体積比が2種類に分けられることを知らない
・体積を公式でとらえている
体積は公式ではなく「イメージ」でとらえると理解が進みます。紹介したコツも押さえることで、体積、そして立体図形の苦手意識も減っていくことでしょう。問題を解きつつ、得意な単元としていってくださいね。
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

