「比例が苦手」を克服する方法

算数の関門の1つ「比の計算」。多くの子供が苦手にする単元です。また「割合」「速さ」などの基礎になる単元でもあります。「比例」の理解が曖昧であると、今後あらゆる単元でつまずくといっても過言ではありません。「比例」を基礎からの正しく理解し、応用力をつけていくために必要な学習法をまとめました。

最重要!! 徹底的に「比例の感覚」を身体に叩き込む

まずは「2つの数が比例する」ことを感覚的に理解できるようになることが最重要。コツをつかんだら何度も反復練習をして、「比例の感覚」を身体に叩き込みましょう。

「比例の表」をマスターしよう

下のような比例の表を使います。AとBが比例するとき、表の空欄を埋めていきましょう。

まずはA=1のときのBの値がわかっているパターン。比較的簡単にできると思います。

少し変化させてみるだけでもよいトレーニングになります。

比例への苦手意識がある段階では、教科書でも問題集でも、比例する2つの数が出てきたときはとにかくこの表を書く癖をつけましょう。慣れたら表を書かなくても大丈夫になるので、最初の段階では徹底して表を書くことが大切です。

ゲーム感覚で反復練習

感覚的に理解するためには、反復練習が必要不可欠。反復するためにはゲーム感覚で取り組むのが一番です。

たとえばタイマーを使って制限時間を設けるのが有効です。「考えればわかる」レベルでは応用はききません。「直感的に、手を止めないで表を埋めることができる」レベルを目指してください。

時間制限を設ける最大のメリットは、自然と早く計算するための工夫を考える習慣がつくことです。

たとえば、下のように最後A=6に対応するBの数を考えたとします。

普通に考えると、15×6=90と求めるところですが、繰り上がりの筆算が必要になりそうですよね。でも前の計算でA=3のときB=45になっていることを利用すると、

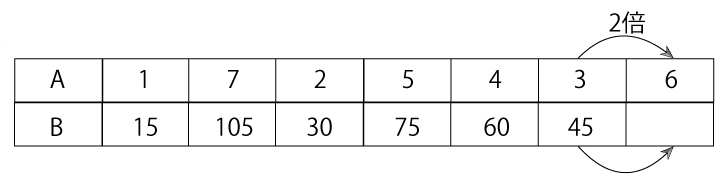
45×2=90と暗算で求めることができますね。

比例の表で「1」をつくろう

上の例でもわかったように、比例の表では「1」対応する数がとても大切です。「1」のある比例の表で比例の感覚がつかめてきたら、今度は「1」がない比例の表に挑戦しましょう。

比例の表に「1」がないときは……

発展的な問題になると、比例の関係で「1」に対応する量が与えられていない場合があります。たとえば次の問題を考えましょう。

まずは比例の表に数字を書き込みます。

次にA=1のときのBの値を求めましょう。

30÷2=15なので、B=15とわかりますね。

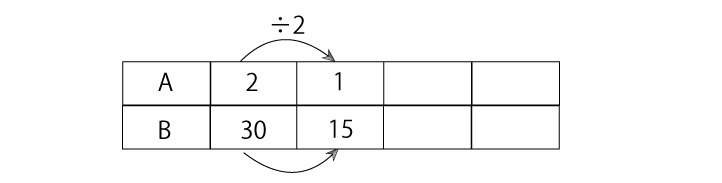
あとは比例の感覚にしたがって、求めたい量を求めればOKです。

「もとにする量」の「もと」とは「1」のことである

このように比例では「1」に対応する量を求めるのが重要です。

そしてこの考え方は「割合」の単元でも非常に重要になる考え方です。

「割合」では「もとにする量」という考え方がでてきます。「もと」とは漢字で「元」と書きます。平成元年といったら、平成1年を意味しますね。つまりこの「もとにする量」とは「1にする量」という意味なので、この比例の考え方を応用したものに過ぎません。

正しく意味を理解できていれば用語に振り回されず、本質的な理解ができるようになるのです。

計算を工夫しよう

ここまでできるようになれば、基本的な比例の計算は暗算でできるようになっているはずです。実際の問題でどのように考えればよいかみていきましょう。

分数計算で一発で求める

おもりの個数と重さは当然比例します。もちろん比例の表を作れば一発ですが、

「比例の表で『1』をつくる」すなわち「1個あたりの重りの重さを求める」ことが最重要とわかっていれば、

120÷3×5=200gと求めることができます。

もちろん慣れてくれば、120×\(\frac{5}{3}\)=200と分数を用いて計算するのがベターです。「×\(\frac{5}{3}\)」が「3で割って5倍すること」と感覚的に理解できるようになれば、どんどん分数をつかって式を書くようにしましょう。

計算に惑わされず、意味を確認しよう

分数計算では分母と分子の数字を逆にしてしまう間違いに注意です。

たとえば前の問題で、120×\(\frac{3}{5}\)=72gとしてしまう誤答は後を絶ちません。

もちろん比例の表で「1」をつくる感覚があればこのような間違いは起こらないはずなのですが……。

このようなミスを減らすために、「増えるか減るかチェック」をするのが有効です。

おもり3個で120g、これを5個にするのだから答えは120よりも大きな数字になるはずですね。72は120よりも小さいので、明らかな間違いだと気付けます。

比例の基礎を固めれば、応用も楽しめる

比例の計算はあらゆる単元の基礎になる分野なので、その場しのぎではない、本質的な理解が求められます。「なんとなく」「公式を習ったから」のような曖昧な理解では確実に先の単元でつまずきます。基礎さえしっかりとしていれば、応用問題はどんどん楽しくなるのが算数というもの。何度も比例の表を書いて、基礎固めをするようにしてください。

※記事の内容は執筆時点のものです