
規則性の問題にはパターンがある? 数列・周期・N進法を理解して苦手を克服
中学受験算数では規則性の問題がよく出ます。その中でも代表的なのが「数列」「周期」「N進法」の3パターンです。今回はこれらの特徴をそれぞれ解説し、具体的な問題とその解き方を紹介します。
【規則性の問題パターン1】数列
規則性の問題で一番多いのが数列です。図形問題の中にも数列が隠れていることがあります。
数列の特徴
数列とは、ある規則に従って順番に並んだ数の列です。中学受験でよく出るのは、ある数に同じ数を次々と加えていく等差数列です。以下は奇数の数列ですが、これは初めの数1に次々と2を加えていった等差数列です。
1、3、5、7、9、…
等差数列の初めの数を「初項」、加える数を「公差」といいます。また、等差数列のN番目の数と、1~N番目の数の和について、それぞれ次の公式が成り立ちます。
N番目の数=初めの数+加える数×(N-1)
1~N番目までの数の和=(初めの数+終わりの数)×N÷2
等差数列以外にも、初めの数に同じ数を次々とかけていく等比数列や、前の2つの数の和を並べたフィボナッチ数列などがあります。
数列の問題
【問題1】長さ5cmの長方形の紙をつないで1本のテープを作ります。のりしろを1cmとして紙を20枚つないだとき、テープの長さは何cmになりますか。
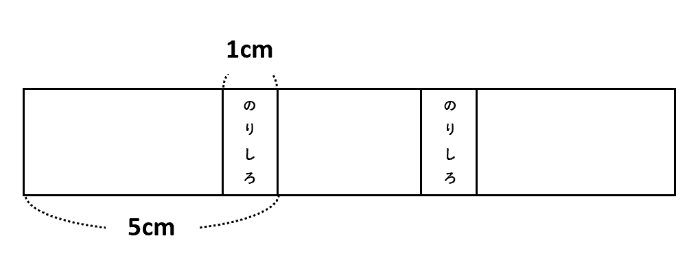
一見すると図形問題のようですが、まずは与えられた図を見ながらテープの長さを書き出していきましょう。
- 紙1枚…5cm
- 紙2枚…9cm
- 紙3枚…13cm
テープの長さは、初めの数が5、加える数が4の等差数列になっています。したがって、紙を20枚つないだときのテープの長さは、等差数列の公式から5+4×(20-1)=81(cm)です。
【規則性の問題パターン2】周期
くり返しのある規則性の問題では周期に注目するのがポイントです。
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます


