仕事算ってどんなもの？ 仕事算をわかりやすく解説

算数が嫌いな子供が苦手とする分野のひとつに「仕事算」があります。仕事算はどのような難易度の中学校でも出題される可能性があるため、中学受験をするうえで避けては通れない単元です。そこで、仕事算の基本的な解き方と、子供がつまずきやすいポイント・対策について解説します。

仕事算とは？ 中学受験ではどのような扱い？

仕事算とは、何人かの人が一緒に仕事をし、何日で完成するかを問う問題です。「公約数と公倍数」「分数」「割合と比」を使って解くため、まずはこれらの分野の計算がしっかりできるようにしておきましょう。

ベーシックな仕事算は、計算問題などとともに得点源の問題として出題されることがあります。また、仕事算の問題は応用がききやすいため、上位校では難しめの文章題として出題されることもあります。そのため、仕事算の基本的な解き方はすべての受験生がマスターする必要があるのです。

仕事算の基本的な解き方解説

次の例をもとに、仕事算の基本的な解き方をおさえましょう。仕事算には、「分数を使う方法」と「公倍数を使う方法」の2つの解き方があります。

仕事算の解き方その1 ――分数を使う方法

まず、仕事の全体量を「1」とおきます。

あきら君は「1」を10日かけて終わらせるので、1日で

の仕事をします。

一方、ゆうかさんは「1」の仕事を15日かけて終わらせるので、1日で

の仕事をします。

そのため、2人が1日でできる仕事の量は、

となります。

2人で「1」の仕事をするので、全部終わらせるのに、

かかることになります。

仕事算の解き方その2 ――最小公倍数を使う方法

最小公倍数を使って、仕事の全体量を決めましょう。

10（日）と15（日）の最小公倍数は「30」なので、仕事の全体量を「30」とおきます。

次に、1日当たりの仕事量を出します。

あきら君は「30」を10日かけて終わらせるので、1日で

の仕事をします。

ゆうかさんは「30」を15日かけて終わらせるので、1日で

の仕事をします。

つまり、2人で1日にできる仕事は、

です。

2人で「30」の仕事をするので、全部終わらせるのに、

かかることになります。

仕事算で子供がつまずきやすいポイント対策

仕事算で子供がつまずきやすいポイントは、大きく分けて4つあります。

それぞれ、対策を見ていきましょう。

仕事算で子供がつまずきやすいポイント［1］――仕事のイメージがつかめない

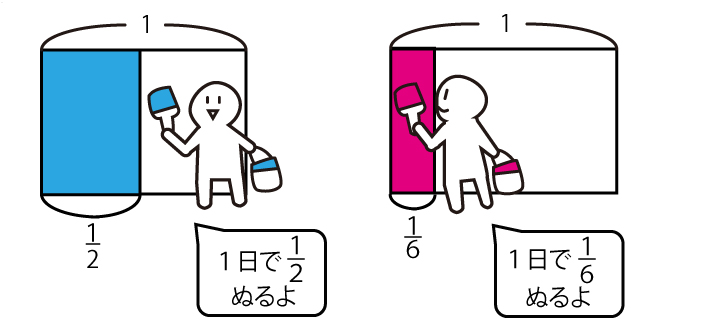
仕事算の典型的な問題は「ある仕事をするのに○○さんは○○（○日、○分など）かかります」といった内容です。そのため、子供によっては問題の状況がつかめないことがあります。まずは、【図1】のように、仕事の具体的なイメージをつけてあげましょう。

仕事算で子供がつまずきやすいポイント［2］――仕事の全体量を決められない

仕事算はまず仕事の全体量を決めるところから始まります。このとき、仕事全体を「1」、または「最小公倍数」とするのがセオリーです。難しい問題であっても、必ず仕事の全体量を決めることころから始めましょう。

仕事算で子供がつまずきやすいポイント［3］――「2人で仕事をする」場合の処理方法がわからない

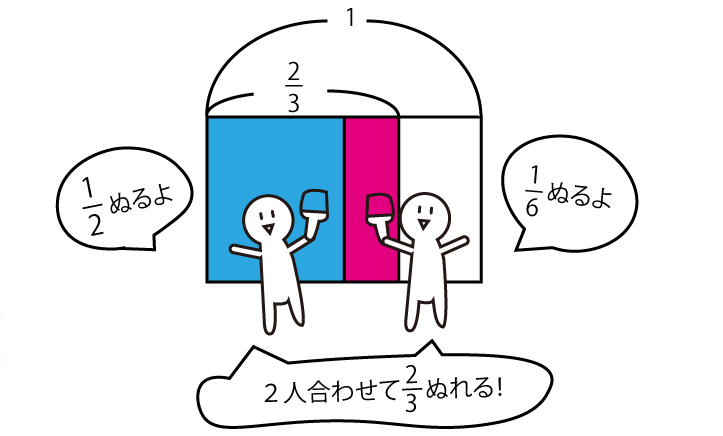
それぞれが1日でできる仕事量を足せば、2人が1日でできる仕事量を求めることができます。この計算そのものは簡単なたし算なのですが、そもそも「2人で仕事をする＝それぞれの仕事量をたす」というのが理解できないことがあります。

【図1】のように、それぞれの仕事のイメージをつかめたら、【図2】のように2人一緒に仕事をしているイメージも与えてあげましょう。

仕事算で子供がつまずきやすいポイント［4］ ――人数が増える、休憩をする、という変形パターンがわからない

応用的な仕事算になると、人数が増えたり、休憩をはさんだり、それぞれ仕事の全体量が変わったりします。これはそれぞれ解法がありますので、まずは［1］~［4］のポイントでひっかかるところがないか、基礎的な仕事算ができているかを確認しましょう。

仕事算は、応用パターンが出題されることもありますが、まずは基礎をおさえることが大切です。簡単な仕事算をくり返し解き、解法を身につけてください。

※記事の内容は執筆時点のものです