台形を対角線で分けてできた三角形を考える！ 面積比を求める方法をわかりやすく解説

台形を対角線で分けると三角形が2つ、または4つできます。これらの三角形の面積（比）を求める問題が中学受験算数ではよく出ます。台形の性質と底辺比・相似比を利用するのがポイントです。

台形を対角線1本で分けるとどうなる？

まずは台形の特徴を復習し、それをふまえて台形を対角線1本で分けてみましょう。

台形はどのような図形か？

台形は、1組の対辺（向かい合っている辺）が平行である四角形です。この平行な対辺が「上底」と「下底」と呼ばれます。「上にある辺が上底で、下にある辺が下底」ではありません。

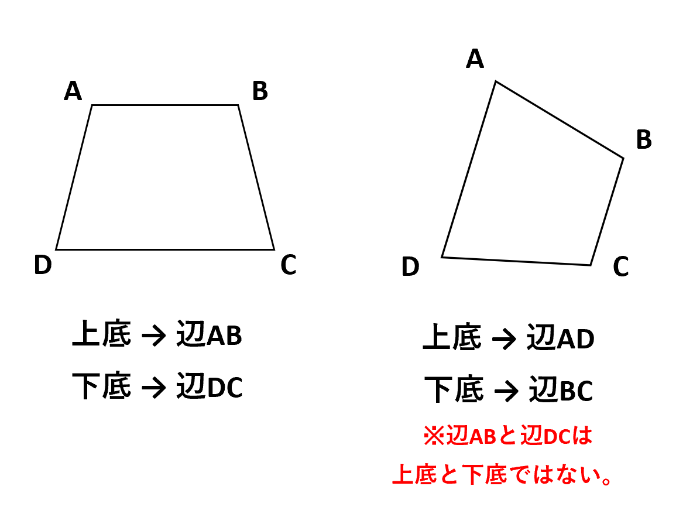
2つの三角形の面積比

台形を対角線1本で分けると、2つの三角形ができます。これらの三角形は、上底と下底をそれぞれ底辺とすると、高さが等しくなります。なぜなら、上底と下底が平行だからです。

高さの等しい三角形は面積比が底辺比と等しくなります。したがって、台形を対角線1本で分けた2つの三角形の面積比は「上底：下底」です。このことをふまえて次の【問題1】を解きましょう。

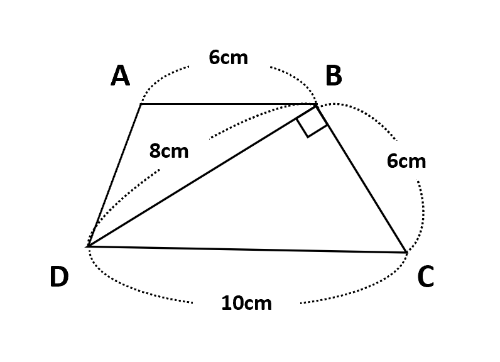
ABとDCが平行なので、四角形ABCDはABを上底、DCを下底とする台形です。また、角CBDが90°なので、三角形BCDはBCを底辺、BDを高さとする直角三角形です。したがって、三角形BCDの面積は6×8÷2＝24（cm\(^2\)）とわかります。

台形を対角線1本で分けた2つの三角形の面積比は「上底：下底」なので、三角形ABDの面積：三角形BCDの面積＝上底：下底＝6：10＝3：5です。したがって、三角形ABDの面積＝三角形BCDの面積×\(\frac{3}{5}\)＝24×\(\frac{3}{5}\)＝14.4（cm\(^2\)）から、四角形ABCDの面積は14.4＋24＝38.4（cm\(^2\)）となります。

台形を対角線2本で分けるとどうなる？

台形を対角線2本で分けると、相似な三角形ができます。そのため、相似比を利用して面積比を求められます。

相似な三角形はどこにできる？

下の図において、ABとDCが平行な台形ABCDを2本の対角線で4つの三角形に分けました。対角線の交点をEとすると、三角形ABEと三角形CDEは相似です。この理由を考えましょう。

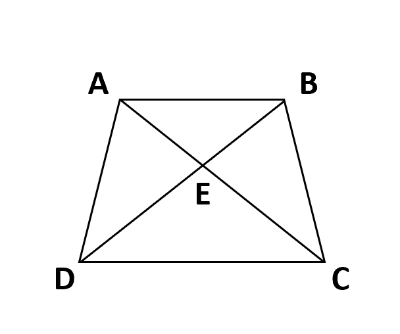
ABとDCが平行なので、平行線の錯角が等しいという性質から、角ABE＝角CDE、角BAE＝角DCEです。「2組の角がそれぞれ等しい」という相似条件が成り立つので、三角形ABEと三角形CDEは相似です。

4つの三角形の面積比

相似な三角形を利用して、台形を対角線2本で分けた4つの三角形の面積を求めてみましょう。