
ニュートン算は難しくない! 水量・行列・牧草の問題には解き方のパターンがある
水の量や人数などが増えると同時に減っている状況を問題にしたのが「ニュートン算」です。
増えるだけ・減るだけの問題よりも難しそうですが、実はパターンを覚えておけば決して難しくありません。今回はニュートン算の代表的な問題をわかりやすく解説します。
ニュートン算の基本的な考え方
ニュートン算の基本的な考え方を復習するため、水槽の水量が変化するタイプの問題を解いてみましょう。
【問題1】50Lの水が入った水槽があります。この水槽の給水管からは毎分3Lで水が入り、排水管からは毎分5Lで水が出ていきます。給水管と排水管を同時に開いておくと、何分で水槽は空になりますか。
【問題1】では、水槽の水が毎分3Lで増えて、毎分5Lで減っています。したがって、5ー3=2から毎分2Lずつ減ると考えれば、50÷2=25(分)で水槽が空になると考えられます。このように、差を利用して計算で解く方法があります。
計算でイメージが湧きにくい場合は線分図を利用するとよいでしょう。もともと入っていた水も増える水も減る水も、すべて一本の線分図に表します。【問題1】では、「もともと入っていた水の量+増える水の量=減る水の量」となります。□分で水槽が空になったとして、以下の線分図を描きました。
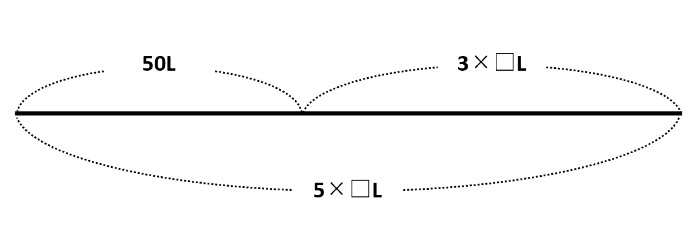
この線分図から、2×□=50であることがわかり、□=50÷2=25(分)を求められます。
ニュートン算の代表的な問題の解き方
ニュートン算の代表的な問題について、線分図を使いながら解いてみましょう。
井戸から水をくみ上げる問題
【問題2】ある井戸には水がたまっていて、一定の割合で水がわき出ています。この井戸を空にするのに、毎分50Lで水をくみ出すと20分かかり、毎分80Lで水をくみ出すと8分かかります。
(1) 井戸は毎分何Lの水がわき出ていますか。
(2) 井戸にたまっていた水は何Lですか。
【問題2】の線分図は以下の通りです。たまっていた水を左端に寄せて、毎分50Lの場合と毎分80Lの場合を2本の直線で表しました。線分の上の○で囲った数字は、毎分1Lで水がわき出るとしたときの増えた水の量です。線分の下には、くみ出して減った水の量を書き込みました。
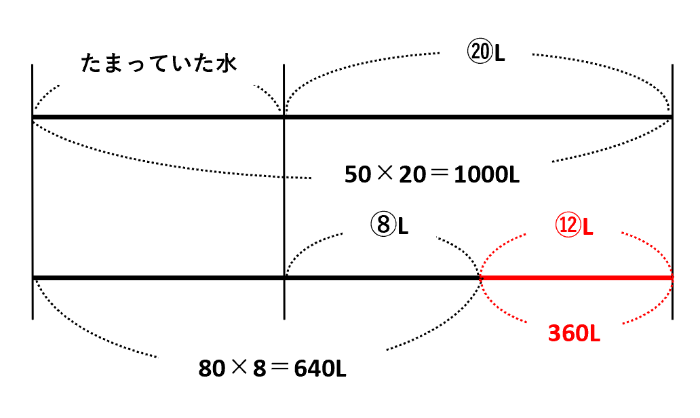
線分図の差(赤い線分)に注目して、⑫=360なので①=360÷12=30となり、(1)の答えが毎分30Lとわかりました。
(2)の答えは、たまっていた水の量=1000-⑳=1000-30×20=400(L)です。
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます


