【算数】3つのポイントをもとに「5種類の四角形」を見分けよう

4年生になると、多くの子が中学受験の準備を始めます。そして算数では、基礎中の基礎ともいえる図形の単元が登場します。

そう、四角形ですね。

小学校では5種類の四角形が登場しますが、これらを見分けることはできますか？

今回は5種類の四角形を見分けるための「3つのポイント」を紹介しつつ、中学入試で活かせる四角形の知識についても解説します。

5つの四角形

まずは、中学受験に登場する四角形の全体像をつかみましょう。

次の図をもとに、一般的な（ノーマルな）四角形に条件を追加していくことで、名前のついた“特別な四角形”ができあがる、という様子をイメージしてみてください。

5つの四角形は、それぞれ包含関係にあります。

たとえば平行四辺形は「台形」の一種です。そして長方形は「平行四辺形」の一種といえますね。

正方形は「ひし形」の一種でもあり、「長方形」の一種でもあり、さらには「平行四辺形」と「台形」の一種、ともいえるのです。

1、台形

はじめに登場する“特別な四角形”は「台形」です。

四角形には4つの辺があり、対面する辺が2対ありますよね。なんの変哲もない四角形のうち、対面する1対の辺が平行な場合は「台形」と呼ばれます。

2、平行四辺形

四角形には対面する辺が2対あり、ひとつの対だけ平行な場合には「台形」ですが、ふたつの対とも平行な場合は「平行四辺形」と呼ばれます。

3、ひし形

ふたつの対面する辺が平行な場合、その四角形は「平行四辺形」ですが、この平行四辺形の4つの辺の長さがすべて同じ場合は「ひし形」と呼ばれます。

4、長方形

平行四辺形の4つの角度をすべて90度にした形が「長方形」です。四角形と聞くと「長方形」を思い浮かべる子も多いかもしれませんが、実は四角形のなかでもかなり特殊な形なのですね。

5、正方形

平行四辺形のうち、4つの辺の長さが同じで、4つの角度も同じ四角形は何と呼ばれるでしょうか？

ひし形でも、長方形でもありません。この四角形は「正方形」と呼ばれます。正方形は身近な図形ですが、長方形と同じく“超特殊”な四角形なのですね。

3つのポイントで整理しよう

なんの特徴もない四角形に、いくつかの条件を付け加えると「特別な名前」がついた四角形ができあがります。

ところが、この条件がなかなか覚えられないんですよね……。

こうしたときは、3つのポイント（着目点）をもとに整理してみるのがおすすめ。四角形の種類を決定づける条件は、ザックリ整理すると次の3つだけです。とてもシンプルですよね。

ポイント【1】向かい合う辺は平行か

最初に注目したいのが、向かい合う辺が平行かどうか。四角形の種類を見分けるうえで、はじめにチェックしておきたい条件です。

具体的には、次のふたつのうち、どちらのパターンかを確かめることで四角形の名称をある程度絞り込むことができます。

小学生のうちは、条件を言葉で伝えると難しく感じてしまうので、下の図のような「四角形のシルエット」を見せても良いでしょう。こうすることで、平行とはどういうことかを感覚的に理解できるはずです。

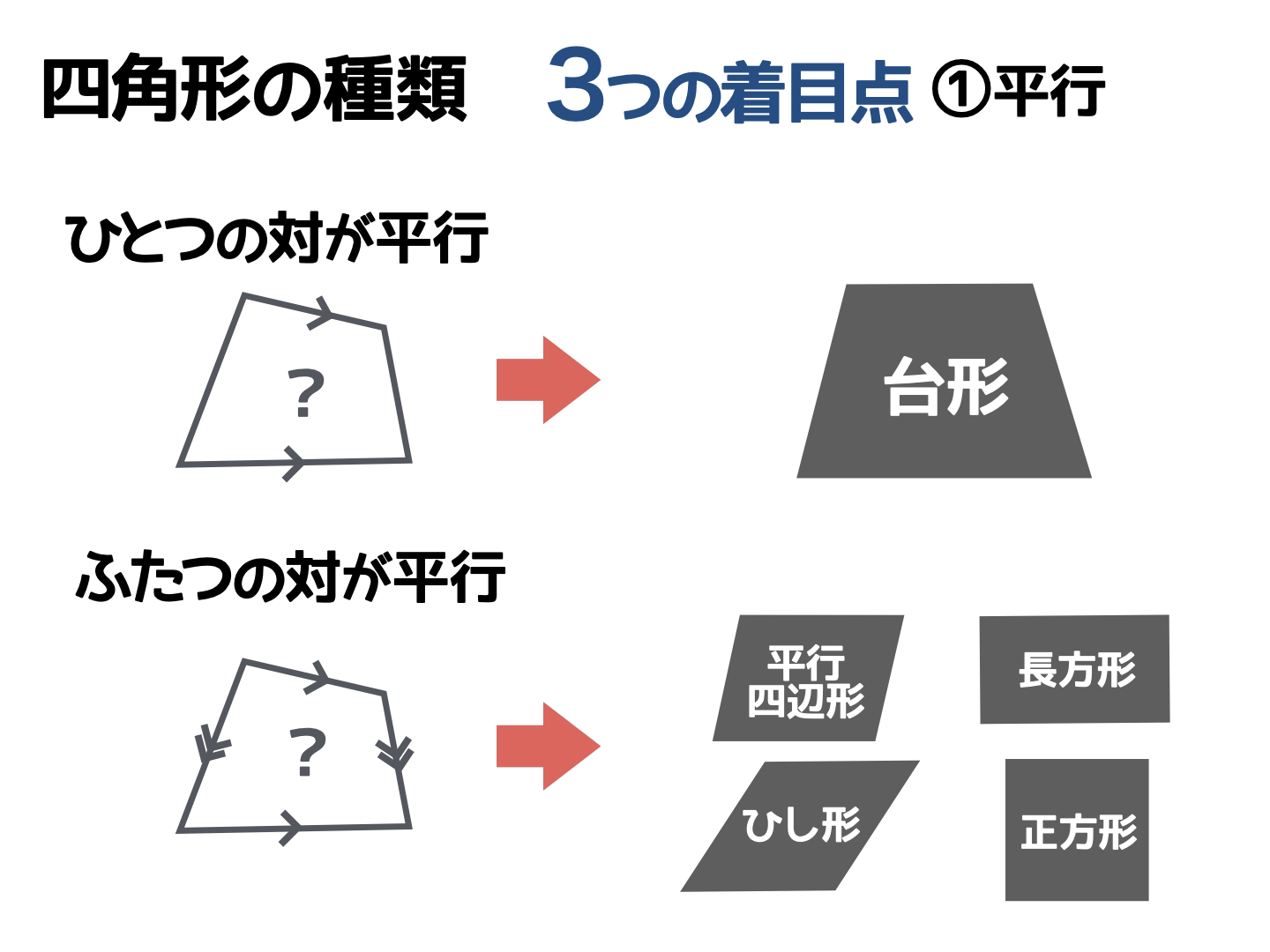
ひとつの対だけが平行

ひとつの対だけ平行な場合、その四角形は「台形」です。シルエットを見ると、上辺と下辺が平行になっていますよね。

一方、左辺と右辺はどうでしょうか？ それぞれ向きがバラバラなため、これは平行とはいえません。

ふたつの対が両方とも平行

ふたつの対とも平行であれば、平行四辺形、ひし形、長方形、正方形のどれか、ということがわかります。シルエットを見ると、どの四角形も上辺と下辺、左辺と右辺の方向がビシッとそろっていることがわかりますね。

なお、平行四辺形とひし形は「斜め」の方向にそろっていますが、長方形と正方形は「垂直」の方向にそろっています。このことを確認することが、この先で四角形の名称をさらに絞り込んでいくときに役立つため、「向かい合う辺は平行か」という条件をはじめにチェックすることが大切なのです。

ポイント【2】4つの辺の長さは同じか

次に注目したいのが、4つの辺の長さが同じかどうか。

4つの辺の長さが同じ四角形として真っ先に思いつくものは「正方形」かと思いますが、実はもう1種類あります。

そう、正方形を“グニャッ”とゆがませた形の「ひし形」ですね。

ポイント【3】4つの角度の大きさは同じか

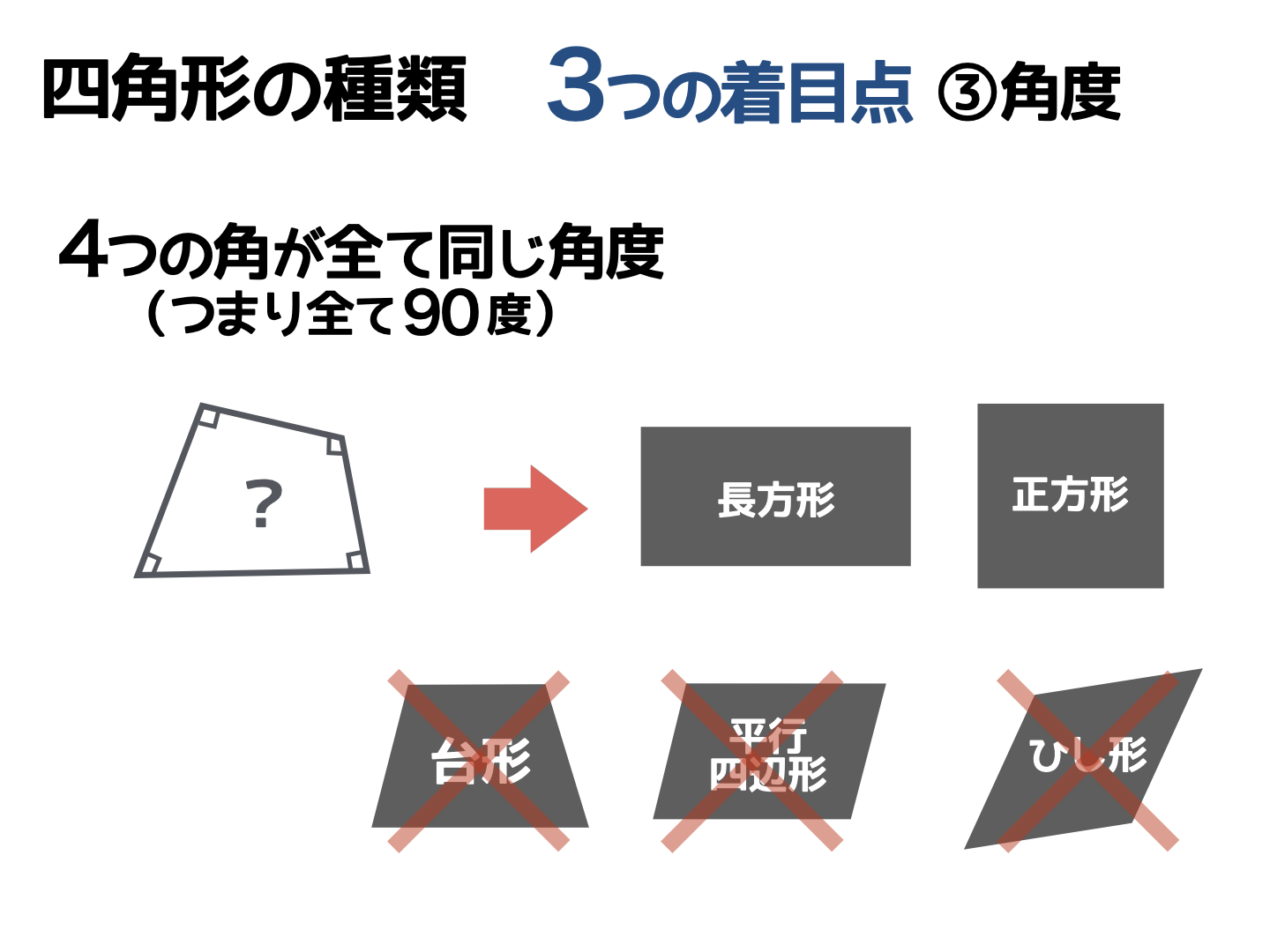
最後に注目したいポイントは、4つの角度の大きさが同じかどうか。

4つの角度が同じということは、すべての角度が90度ということ。90度は「直角」ともいいますね。

そして4つの角度がすべて同じ四角形は、たった2種類しかありません。それは、長方形と正方形です。

ちなみに世の中にある四角形には、長方形か正方形のものが多く見つかります。街にあるビルやその窓、家のなかにあるドアやテーブルなど、そのほとんどが長方形や正方形です。

中学入試に活かせる知識

四角形の種類を見極めるための「3つのポイント」を紹介してきました。実はとてもシンプルに見分けることができる、と感じたのではないでしょうか？ 先ほど紹介した表の理解度も、グッと上がっているはずです。

では最後に、中学受験の算数において、四角形の知識がどのように応用できるかをお伝えします。

四角形には「並行線」がたくさんある

四角形の種類を見極める条件として重要な条件は「対になる辺が平行かどうか」ですが、平行という言葉で思いつくことはありませんか？

そう、対頂角や同位角、錯角ですね。

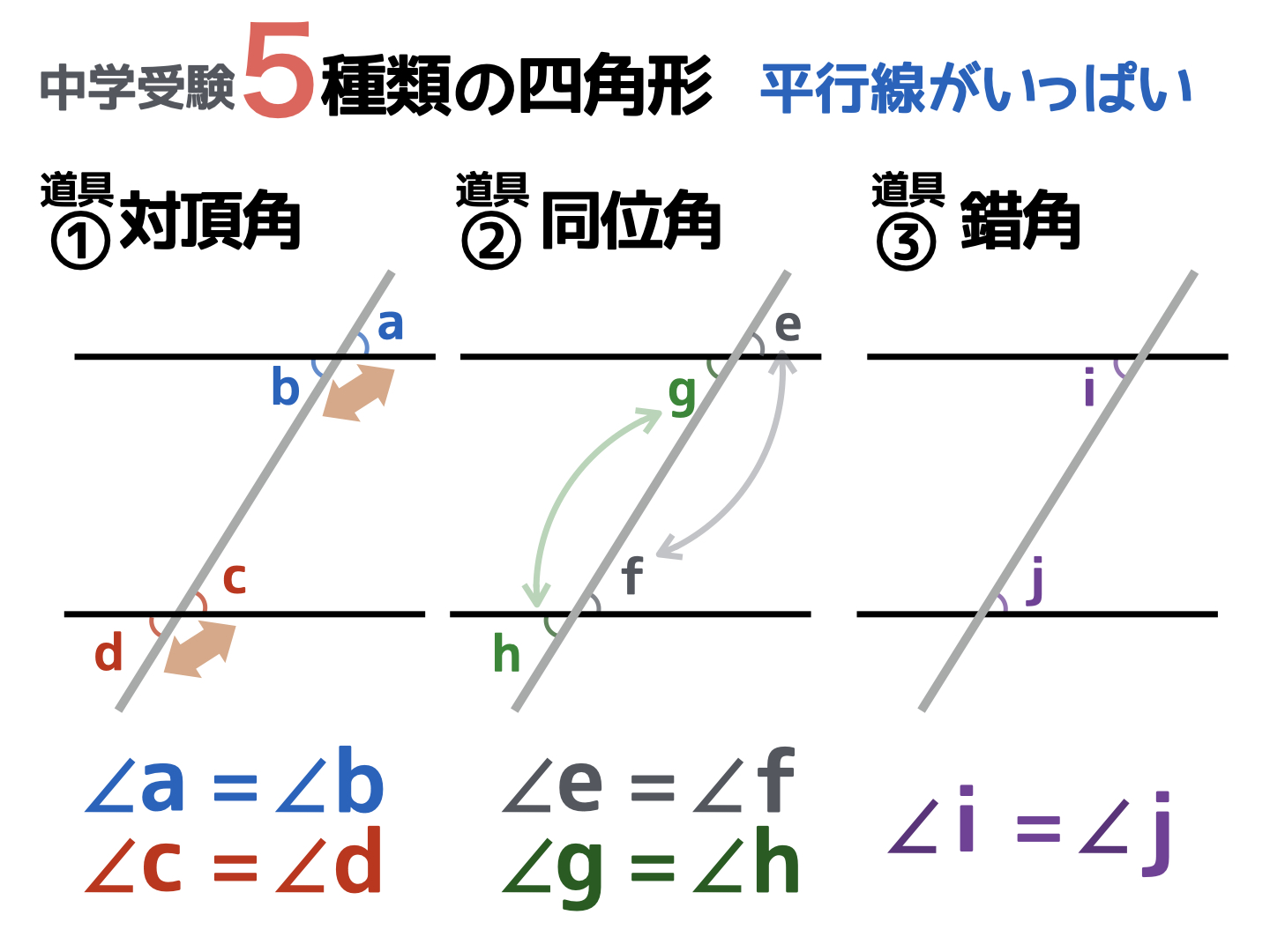
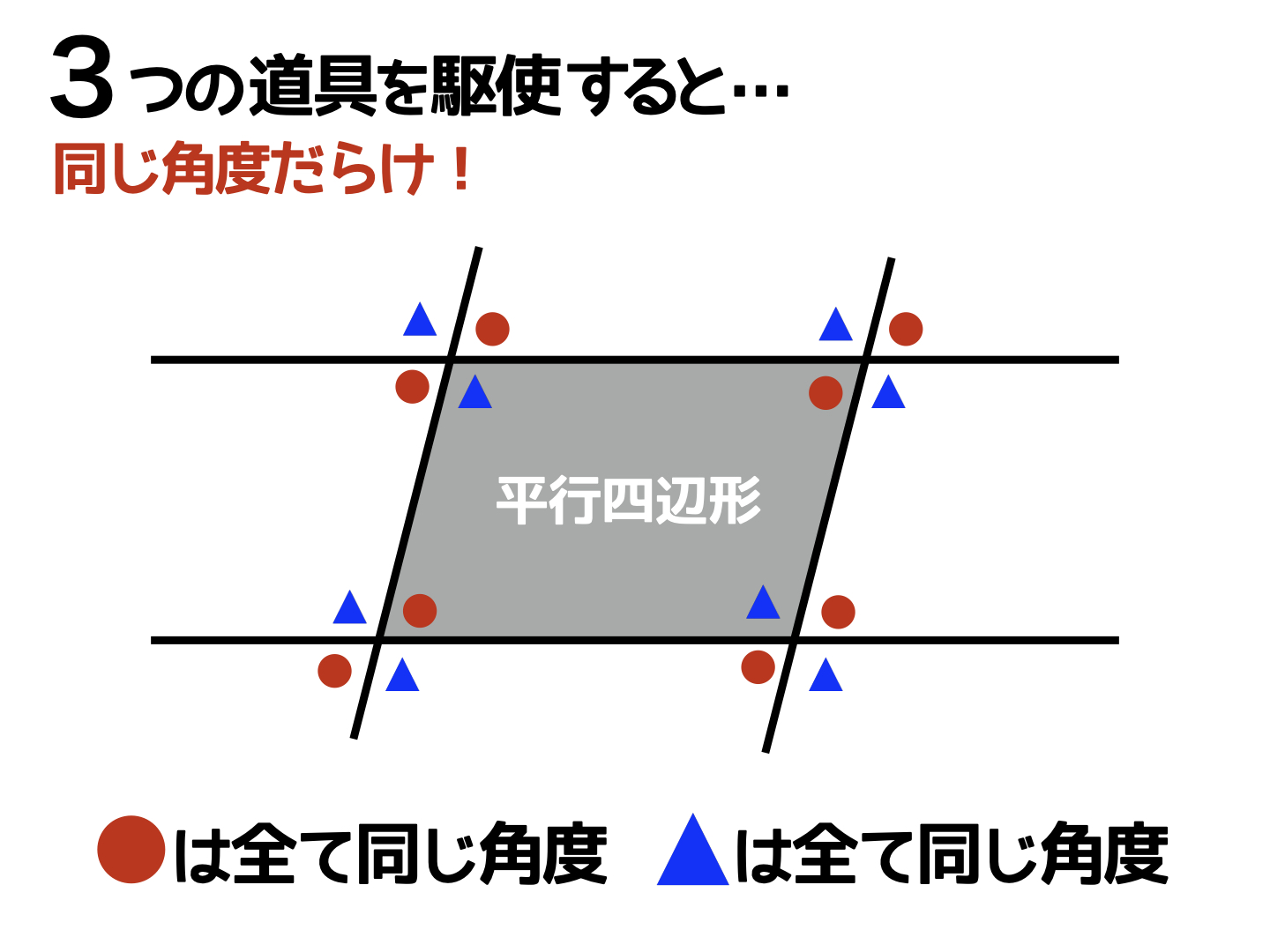
四角形に平行な線があれば、まずは「同じ大きさの角度が多く見つかるはず！」と考えてみましょう。対頂角・同位角・錯角の「3つの道具（3つの角度）」がそれぞれ同じ大きさであることを知っていると、平行四辺形には同じ大きさの角度がたくさんあるということも理解できます。

面積の公式は柔軟に使い分ける

「四角形の面積を求めよ」と問われたら、ほとんどの子は面積の公式を思い浮かべるでしょう。長方形であれば「たての長さ×よこの長さ」みたいなものです。

でも、すべての四角形は次のような包含関係にありましたよね。

たとえば正方形は長方形の一種ともいえますし、ひし形の一種ともいえます。そのため正方形の面積を求めるときに、長方形の面積の公式を使っても、ひし形の面積の公式を使ってもOKということ。

小学生は、四角形の種類と、その面積の公式が1対1で対応しているように思えるようですが、あまり公式にとらわれず、柔軟に考えるようにしたいですね。

まとめ

中学入試で高い確率で出題され、合否にも影響する「図形問題」。今回は、その入門編ともいえる「四角形」について解説しました。

まず身につけたいのが、なんの特徴もない四角形に条件を加えていくことで“特別な名前”がつけられていくという感覚です。

そして四角形の種類を決定づける条件は、次の3つのポイントに集約できます。

小学生で登場する「5つの四角形」を正しく理解しつつ、受験算数を攻略していきましょう！ 

※記事の内容は執筆時点のものです