拡大図と縮図で大切な「縮尺」とは何か？ 地図の問題は相似の考え方で解ける
中学受験算数でとても大切な「相似」は、学校の算数では6年で「拡大図と縮図」として学びます。入試では、典型的な相似の問題ではなく、地図を題材とした拡大図と縮図の問題が出ることもあります。中学受験算数と学校の算数をしっかり結び付けて理解しましょう。
Contents
拡大図と縮図で大切な「縮尺」
拡大図と縮図では、相似比は「縮尺」と呼ばれます。中学受験塾では相似を教えるときに縮尺も一緒に教えるので、受験生は5年で縮尺に触れるはずです。
縮尺とは何か？
実物を小さくして地図などに表すとき、実物の長さをどれほど短くしたかを表すのが縮尺です。対義語の「現尺」は、実物と同じ長さを図に表すときに使います。
縮尺は実物の長さに対する図での長さの割合なので、「\(\frac{図での長さ}{実物の長さ}\)」で表します。たとえば、縮尺が\(\frac{1}{10000}\)の地図では、100m（10000cm）の道路が1cmの長さで描かれます。また、\(\frac{1}{10000}\)は1:10000という比で表されることもありますが、分数も比も同じ縮尺なので混乱しないようにしましょう。
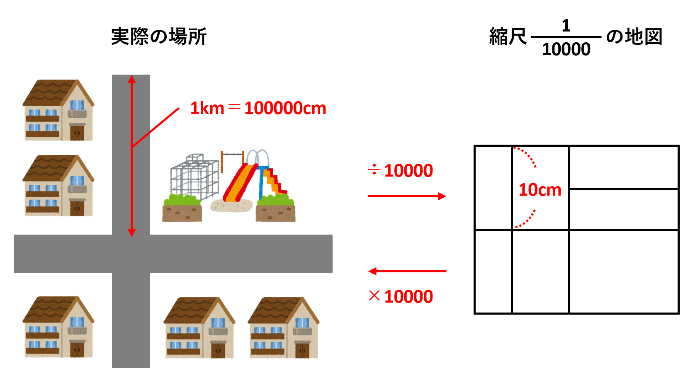
縮尺と距離・面積
縮尺と距離・面積の関係を次の【問1】で考えてみましょう。
【問1】縮尺\(\frac{1}{50000}\)の地図があります。
(1) この地図上で6cmの距離は、実際には何kmですか。
(2) 2.5kmの距離は、この地図上では何cmですか。
(3) この地図上で10cm\(^2\)の面積は、実際には何km2ですか。
(1)は、6cm×50000＝300000cm＝3kmです。
(2)は、2.5km＝250000cmなので、250000cm÷50000＝5cmです。
50000をかけるのか割るのか混乱することもあるかもしれません。「縮尺をかけるのは拡大したいときで、割るのは縮小したいとき」と覚えておけば混乱を防げます。
しかし、(3)も(1)と同じように考えて、10cm\(^2\)×50000＝500000cm\(^2\)とすると間違いです。
たとえば、10cm\(^2\)を縦2cm、横5cmの長方形とすると、縦と横のそれぞれを50000倍しなければなりません。
したがって、10cm\(^2\)＝2cm×50000×5cm×50000＝10cm\(^2\)×50000×50000＝25000000000cm\(^2\)＝2.5km\(^2\)が正解です。
面積の場合は、縮尺を2回かけたり割ったりする必要があります。
拡大図と縮図は入試問題としてどう出る？
拡大図と縮図は入試問題として出る場合、学校のテストよりもやや難しくなります。
単位換算の問題
【問2】縮尺\(\frac{1}{25000}\)の地図で10cm\(^2\)の面積は、実際には何haですか。
10cm\(^2\)を実際の面積に変換すると、10cm\(^2\)×25000×25000＝6250000000cm\(^2\)です。
1a＝100m\(^2\)＝1000000cm\(^2\)、1ha＝100a＝1000000cm\(^2\)×100＝100000000cm\(^2\)なので、6250000000cm\(^2\)＝62.5haが答えです。
面積なので縮尺を2回かけた上で、cm\(^2\)をhaに変換します。aとm\(^2\)、aとhaなどの単位換算に不安がある場合は復習しましょう。
速さから縮尺を求める問題
【問3】時速50kmの車で走ると12分かかる距離は地図上で20cmです。この地図の縮尺は何分の1ですか。
速さから縮尺を求める問題では、最初に実際の距離を求めます。「速さ×時間＝距離」なので、12分＝\(\frac{12}{60}\)時間＝\(\frac{1}{5}\)時間として、時速50km×\(\frac{1}{5}\)時間＝10km＝1000000cmです。
1000000cmが20cmになっているので、\(\frac{20}{1000000}\)＝\(\frac{1}{50000}\)（50000分の1）が答です。
距離から面積を求める問題
【問4】長方形の土地の周りを時速45kmの車で一周すると40分かかります。この土地の縦の距離が縮尺\(\frac{1}{50000}\)の地図上で12cmのとき、この土地の面積は何haですか。
「速さ×時間＝距離」なので、40分＝\(\frac{40}{60}\)時間＝\(\frac{2}{3}\)時間として、時速45km×\(\frac{2}{3}\)時間＝30kmが土地の周りの長さです。1周が30kmなので、縦と横の和は30km÷2＝15kmとわかります。
次に、縮尺\(\frac{1}{50000}\)の地図上で12cmの距離は、実際は12cm×50000＝600000cm＝6kmです。縦の距離が6kmなので、横の距離は15－6＝9kmと求められます。したがって、土地の面積は6km×9km＝54km\(^2\)です。1km\(^2\)＝100haなので、54km\(^2\)＝5400haが答えです。
拡大図と縮図は社会の地理でも必要
縮尺については、算数だけでなく、社会の地理でも必要となることがあります。社会の計算問題としても出やすいので、単位換算も含めて、できるようにしておきましょう。
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます
