
「反比例が苦手」を克服する方法
反比例は比例と同様、今後の学習の成果に直結する非常に重要な考え方です。たとえば「速さ」が苦手な子供はよくよく原因を探ると反比例の理解が不十分であることが少なくありません。どのレベルまで理解しておけば十分なのか、まとめました。
Contents [hide]
反比例の感覚を身体に叩き込む
「比例」を理解できたら、次は反比例。小学生で出てくる関数はほぼ比例と反比例に集約されます。2つの特徴は、理屈はもちろん「直感的に」わかる状態まで理解を深めておく必要があります。
「反比例の表」をマスターしよう
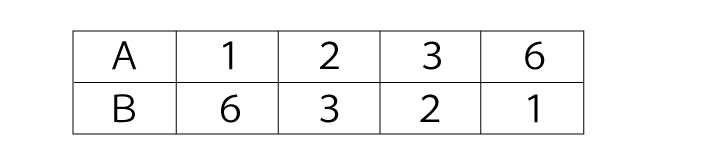
下のような反比例の表を使います。AとBが反比例するとき、表の空欄を埋めていきましょう。「Aが●倍になったら、Bは1/●倍」になるルールを確認しながら進めてください。
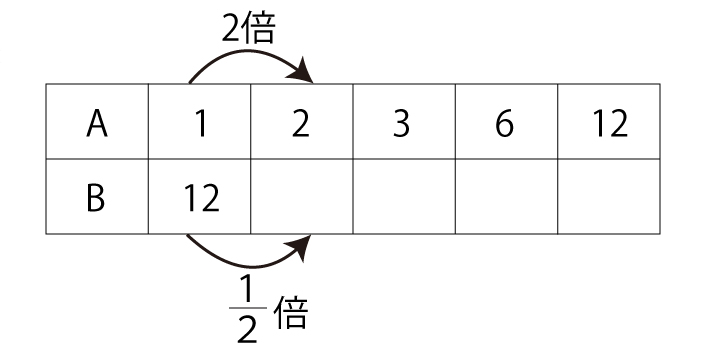
慣れてきたら、分数が登場するものも積極的に扱いましょう。
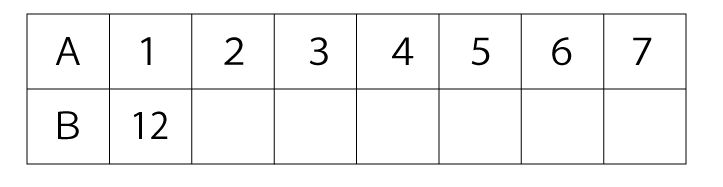
身近なもので理解することも大切ですが、表を使って理解する方が近道であることが実は多いです。
反比例に慣れてきたら一段追加!
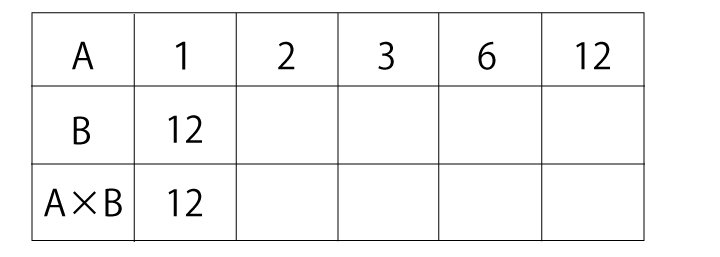
上のように1段「A×B」の行を追加します。もちろんAとBが反比例の関係にあるとき、A×Bの値は一定になりますね。このように作業を通して段階的にA×Bの値が一定になることを理解することが大切です。完成した表は下のようになりますね。
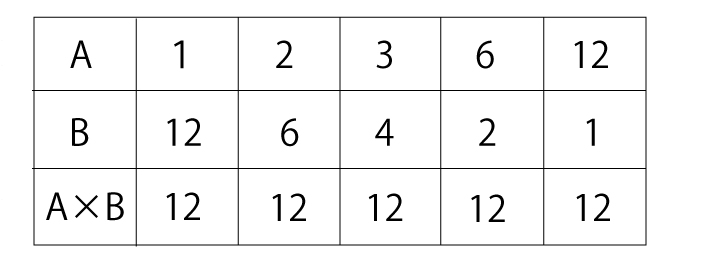
「速さ」の復習に用いる
小学校のカリキュラムでは「速さ」を習ったあとに「反比例」を学習することが多いです。しかし実は「反比例」を習ったあとでこそ、「速さ」への理解が深まることが多いのです。
反比例の表を速さの表に
上の表はまさに「速さ」「時間」「距離」の3つの関係です。
実際に書き込んでみると下のようになります。
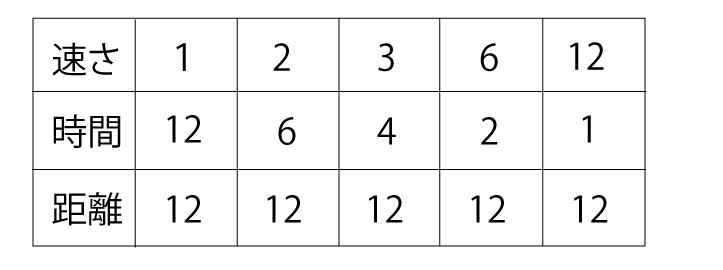
反比例の感覚がある子であればすぐに3つの数の関係性を理解できると思います。
速度の問題は「公式」に頼らない
「は・じ・き」公式というものを聞いたことがあるかと思います。「速さ・時間・距離」の頭文字をとったものですね。速度の3量の関係を便宜的に覚えてしまおうという公式です。
これはもちろん便利な公式なのですが、公式から理解してしまうと、理解が表面的になり、応用問題に太刀打ちできません。
「反比例の感覚を叩き込む」→「速度の3量(速さ・時間・距離)の関係を(直感的に)理解する」の順番を大切にしてもらいたいと思います。
反比例のグラフに強くなる
グラフは視覚的に関数をとらえるのに有効です。反比例のグラフは「初めて見る変な曲線」が登場します。慣れておくことが今後の複雑な関数の学習への苦手意識の克服につながるでしょう。
反比例のグラフは「なめらかに」
比例のグラフは「定規で」直線を描けばよいものでした。一方反比例のグラフは定規を使いません。通る数点をフリーハンドで「なめらかに結ぶ」能力が求められます。
この反比例の表に基づいてグラフを描くと下のようになります。
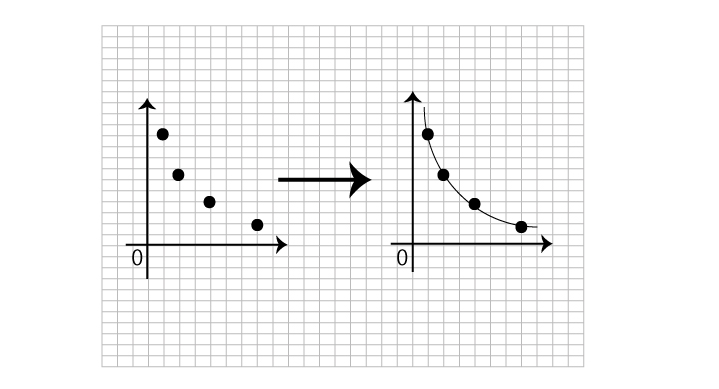
グラフをなめらかに描く能力は、今後の学習に大きく影響します。定規では簡単に描けても、フリーハンドで描くのが苦手な子供がいます。その場合、グラフを描くのが億劫になり、関数の学力低下に直結するのです。
長方形をかきこむ
最後に1つ、グラフに「長方形を描く」学習法を紹介します。
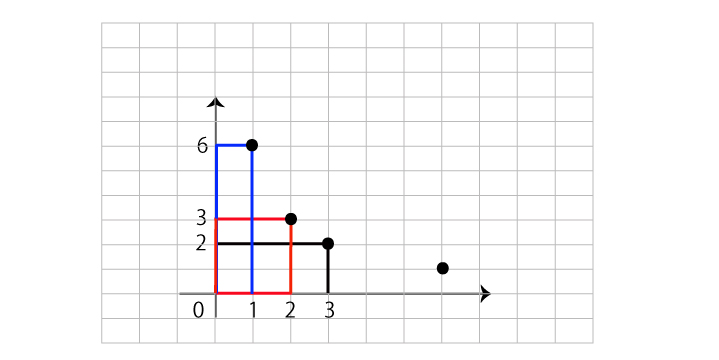
図のように、グラフを描くときに書き入れた点で長方形をつくります。図でできた3つの長方形の面積はそれぞれどうなっているでしょうか。
青の長方形は縦が6、横が1なので面積は6×1=6ですね。
同様に赤は2×3=6、黒は3×2=6となり、すべて面積が6になりますね。
これは表で「A×Bは一定」であることを図で確認したものです。表による表現とグラフによる表現の関連性を知ることで、応用力はどんどん高まっていくでしょう。
基礎は「できる」ではなく「早く、直感的にできる」ことが大切
反比例は今後の学習につながる基礎です。なんとか「できる」のレベルではなく、「早く、直感的にできる」レベルになるように、本記事を参考に反比例の苦手克服に取り組んでみましょう。
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

