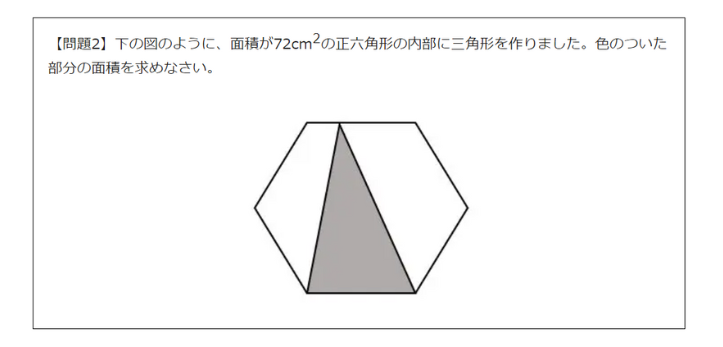
周りの長さの求め方を理解しよう! 四角形やおうぎ形を組み合わせた図形を考える
算数の図形問題では、図形の周りの長さを求めなければならないことがあります。円周の長さを求める公式はありますが、他の図形については公式がありません。そのため、図形の周りの長さを求める問題に苦手意識のある中学受験生もいるでしょう。今回は、そんな受験生のために、図形の周りの長さの求め方を整理して紹介します。
Contents [hide]
基本的な図形の周りの長さの求め方
周りの長さを求める問題を解くためには、基本的な図形の周りの長さの求め方を正しく理解することが大切です。
四角形の周りの長さの求め方
四角形の中でも特に基本的なのが長方形と正方形です。長方形は、内角が全て直角になっている四角形で、向かい合う辺の長さは同じです。そのため、「長方形の周りの長さ=(縦+横)×2」が成り立ちます。一方、正方形は、4つの辺の長さが同じ長方形です。そのため、「正方形の周りの長さ=一辺×4」が成り立ちます。
特に正方形の周りの長さは、公式として覚えるよりも、意味を理解しましょう。そうすれば、「正N角形の周りの長さ=一辺×N」もわかります。中でも、円に内接する正六角形の周りの長さは「一辺=半径」なので「正六角形の周りの長さ=一辺×6=半径×6=直径×3」と表せます。
円とおうぎ形の周りの長さの求め方
円周の長さについては、円周率の定義から「円周の長さ=直径×円周率=半径×2×円周率」です。この式は覚えておかなければなりません。
おうぎ形は円の一部を切り取った図形なので、おうぎ形の弧の長さは中心角の大きさに比例します。そのため、「弧の長さ=円周の長さ×\(\frac{中心角}{360°}\)=直径×円周率×\(\frac{中心角}{360°}\)=半径×円周率×\(\frac{中心角}{180°}\)」が成り立ちます。
弧の長さの求め方さえわかれば、「おうぎ形の周の長さ=弧の長さ+半径×2=弧の長さ+直径」となることもわかるでしょう。この式をわざわざ覚える必要はありません。
複雑な図形の周りの長さの求め方
一見すると複雑な図形も、基本的な図形の組み合わせに過ぎません。そのため、基本的な図形を見つけることが大切です。
でこぼこした図形の周りの長さの求め方
【問題1】下の図は、大きな長方形から小さな長方形を切り取ってできた図形です。この図形の周りの長さを求めなさい。

【問題1】のように、でこぼこした図形の周りの長さを求める場合、一部の長さを移動して基本的な図形を作れないかどうかを考えることが大切です。
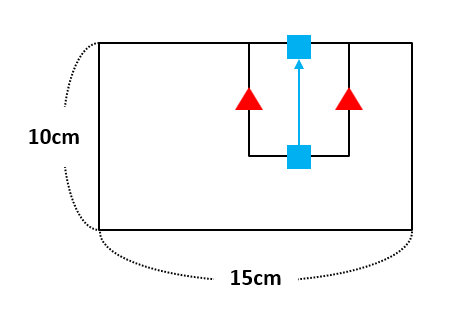
【問題1】では、下の図のように、■の長さを上に移動すると、10cm×15cmの長方形になります。また、▲の長さはどちらも6cmです。したがって、求める周りの長さは、(縦×2+横×2+▲×2)=10×2+15×2+6×2=62(cm)です。
正方形を組み合わせた図形の周りの長さ
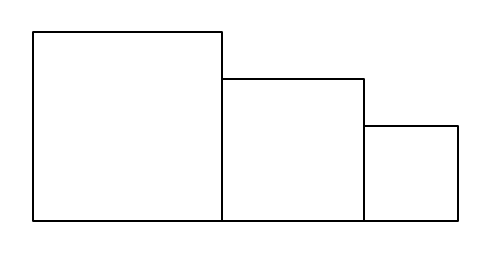
【問題2】下の図は、大中小の正方形を3つ並べてできた図形です。この図形の周りの長さを求めなさい。ただし、大中小の正方形の面積の比が25:16:9で、最も大きな正方形の一辺の長さが15cmです。
【問題2】でも、まずは一部の長さを移動して基本的な図形を作れないかどうかを考えましょう。下の図のように、■と◆を上に移動して、▲と●は右に移動しました。そうすると、求める周りの長さは、縦が大の正方形の一辺、横が大中小の正方形の一辺の和となる長方形の周りの長さに等しいことがわかります。

次に、中小の正方形の一辺の長さをそれぞれ求めます。大中小の正方形は全て相似で、面積の比が25:16:9です。相似な図形では「面積比=相似比×相似比」なので、25:16:9=5×5:4×4:3×3より、大中小の正方形の相似比(=一辺の長さの比)は5:4:3と求められます。大の正方形の一辺の長さが15cmなので、大中小の正方形の一辺の長さは5:4:3=15cm:12cm:9cmです。
したがって、求める周りの長さは(大の正方形の一辺×2+大中小の正方形の一辺の和×2)=15×2+(15+12+9)×2=102(cm)です。
おうぎ形を組み合わせた図形の周りの長さの求め方
【問題3】下の図では、同じ大きさの四分円が正方形の中にあります。色のついた図形の周りの長さを求めなさい。ただし、円周率は3.14とします。
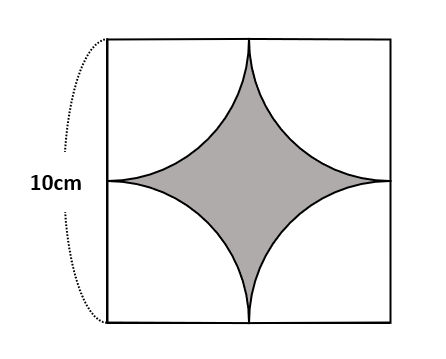
【問題3】では、色のついた図形に注目すると、周りの長さを求めるのが難しそうです。こういう場合は視点を変えましょう。そして、色のついた図形の周りの長さが四分円の弧の長さの和に等しいことに気づけば、あっという間に答えを求められます。(色のついた図形の周りの長さ)=(四分円の弧の長さ×4)=(半径が5cmの円の円周の長さ)=5×2×3.14=31.4(cm)が答えです。

複雑な図形の面積の求め方5選! 分割・移動・等積変形などのパターンを覚えよう
中学受験の算数では、図形の面積を求める問題が頻繁に出ます。しかも、問題となるのは、典型的な多角形や円ではなく、これら...
周りの長さを求めるのに必要なのは「ていねいさ」
複雑な図形の周りの長さを求める場合、どこが「周り」に含まれるのかを適切に把握し、それらを基本的な図形に変形することで、問題を解いていきます。このときに必要なのは、公式などに頼らず図形としっかり向き合う「ていねいさ」です。
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます