周期算で規則性の基礎を固める！ 割り算のあまりから循環小数や日暦算を考える
中学受験生の多くが小学4年で学ぶ特殊算の一つに「周期算」があります。周期算は割り算の商とあまりを利用して解くのが一般的で、慣れるまで難しく感じられるかもしれません。そんな周期算の基礎から応用までをわかりやすく解説します。
周期算の基本問題
周期算の基本問題を通して、周期算で大切な考え方を学びましょう。
周期とは何か？
周期とは、ある現象の同じ状態が繰り返し現れるときの間隔です。多くの場合、時間や期間が「周期」とされます。一方、中学受験算数では、繰り返される数の個数を「周期」といいます。7,8,9,7,8,9,7,8,9,…ならば、7,8,9が繰り返される数でその個数は3個なので、周期は3です。
規則的に並べられた数をグループ分けして考える数列の問題に「群数列」があります。周期算も群数列の一種です。
周期算をどう解くか？
【問題1】ある規則に従って以下のように数を並べました。
2,9,7,2,1,5,2,9,7,2,1,5,2,9,7,…
(1) 左から数えて2024番目の数はいくつですか。
(2) 左から数えて2024番目までに2は何回出てきますか。
(3) 左から数えて1番目から2024番目までの数の和はいくつですか。
問題を見て「繰り返しがある」と気づいたら、必ず周期（繰り返される数の個数）を求めましょう。【問題1】では、2,9,7,2,1,5が繰り返されるので周期は6です。
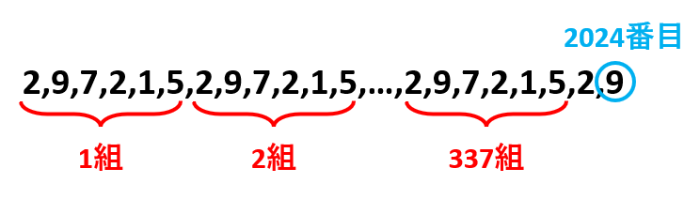
(1) 2,9,7,2,1,5が何組あるかを考えるため、2024を周期の6で割って商とあまりを求めます。2024÷6＝337あまり2より、商から2024番目までに2,9,7,2,1,5が337組あり、あまりから338組の2番目の数が答えだとわかります。したがって、9が答えです。
(2) 2,9,7,2,1,5から2は2回出てきます。(1)の割り算の商より、337組の2,9,7,2,1,5から2は2×337＝674（回）出てくるとわかります。あまりも考えて338組の1番目にも2があるので、674＋1＝675（回）が答えです。
(3) 2＋9＋7＋2＋1＋5＝26が337組あり、これに338組の2＋9＝11を足して、26×337＋11＝8773が答えです。
周期算の応用問題
周期算の応用問題も、割り算の商と余りを利用して解きます。
小数第N位を求める（循環小数）
【問題2】\(\frac{3}{7}\)の小数第50位の数を求めなさい。
とりあえず\(\frac{3}{7}\)＝3÷7を計算してみると、3÷7＝0.42857142…となり、428571が繰り返されることがわかります。このように、小数点以下で同じ数が無限に繰り返される小数を循環小数といいます。一方、円周率の3.141592…は同じ数が繰り返されない無限小数なので、循環小数ではありません。
循環小数の小数第N位を求める問題も周期算の一種です。【問題2】では、428571より周期は6なので、50÷6＝8あまり2を計算します。あまり2から、428571の2番目の数の2が答えだとわかりました。
特定の日の曜日を求める（日暦算）
【問題3】2023年の4月1日は土曜日です。このとき、次の問いに答えなさい。
(1) 同じ年の9月1日は何曜日ですか。
(2) 同じ年の4月1日から12月31日までに水曜日は何日ありますか。
(3) 2024年の4月1日は何曜日ですか。
特定の日の曜日を求める特殊算を「日暦算」といいます。月火水木金土日の7つの曜日が繰り返されることから、日暦算も周期算の一種です。
日暦算は、以下の常識を知らないと解けません。
- うるう年でない年の1年は365日で、原則として1か月は31日。
- 4・6・9・11月は30日。
- 2月は、うるう年でなければ28日、うるう年ならば29日。
- 西暦の年号が4で割り切れる年がうるう年。ただし、100で割り切れて400で割り切れない年はうるう年でない。
2と3を合わせて「に（2）し（4）む（6）く（9）さむらい（士＝11）」と覚えている受験生は多いはずです。
(1) 日暦算の周期は7です。4月1日の土曜日からスタートすると、あまりで次のように曜日がわかります。
あまりが1…土、2…日、3…月、4…火、5…水、6…木、0…金
したがって、2023年4月1日から9月1日までは30日×2（4・6月）＋31日×3（5・7・8月）＋1日（9月1日）＝154日で、154÷7＝22あまり0なので、金曜日が答えです。
(2) 4月1日から12月31日までは30日×4（4・6・9・11月）＋31日×5（5・7・8・10・12月）＝275日で、275÷7＝39あまり2です。4月1日から12月31日までに39週と2日あり、40週目の2日間に水曜日は含まれません。したがって、水曜日は39日あります。
(3) 2024年は4で割り切れる年なのでうるう年です。2024年2月は29日なので、2023年4月1日から2024年4月1日までは365日＋1日（2024年2月29日）＋1日（2024年4月1日）＝367日です。367÷7＝52あまり3なので、月曜日が答えです。
周期算で規則性に慣れる
算数では、周期のような規則性に着目して解く問題が少なくありません。周期算を通して規則性に慣れておけば、数列や方陣算などを解くのが楽になります。小学4年のうちに周期算をたくさん練習しましょう。
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます