計算の工夫の基礎力-計算量を減らしてミスを防ごう!｜中学受験算数の基礎力を伸ばす#15

こんにちは。ドリるゼミ講師のさちです。

今回は「計算の工夫の基礎力」というテーマでお届けします。

お子さまは「計算の工夫」は得意ですか？

計算を工夫すると計算量が減り、ミスの発生確率も下がります。

計算があまり得意ではない・計算ミスが多い子こそ、計算の工夫を習得するメリットは大きいです！

この記事では、以下の3つのポイントに分けて計算の工夫をお伝えしていきますね。

1. 共通の数字でまとめよう
2. 順序を変えよう
3. 10,100,1000を作ろう

1.  共通の数字でまとめよう

1つめの工夫は「共通の数字でまとめる」です！

以下の問題をもとに考えてみましょう。

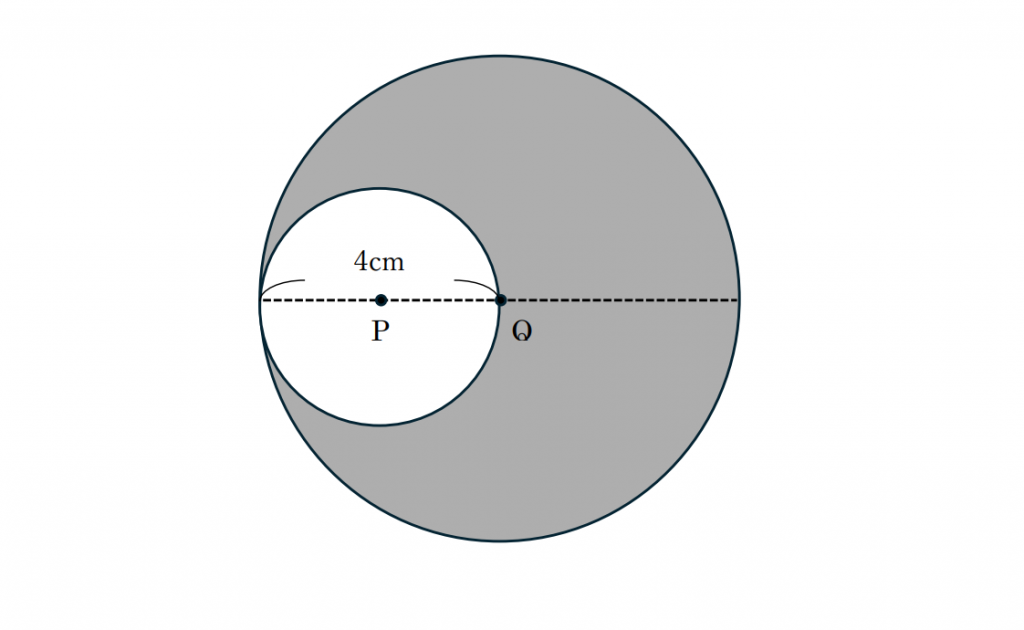
斜線部分の面積は

（大きい円の面積）-（小さい円の面積）

で求められるので、式は

4×4×3.14-2×2×3.14

となります。

この式を

• そのまま計算する
• 共通の数字でまとめる

の2パターンで計算してみましょう。

いかがでしょうか？

共通の数字でまとめると、面倒な3.14のかけ算が1回で済みましたね！

人間は機械ではないので、どんなに気を付けても計算ミスはゼロにはなりません。

計算の回数そのものを減らすことで、ミスの発生確率を減らすことを意識しましょう！

練習問題を用意しましたので、ぜひやってみてください！

解答・解説は以下の通りです。

2.  順序を変えよう

2つめの工夫は「順序を変える」です。

以下の問題をもとに考えてみましょう。

まずは28×9ですが、計算が大変ですよね。

そこで、次のような工夫をしてみましょう。

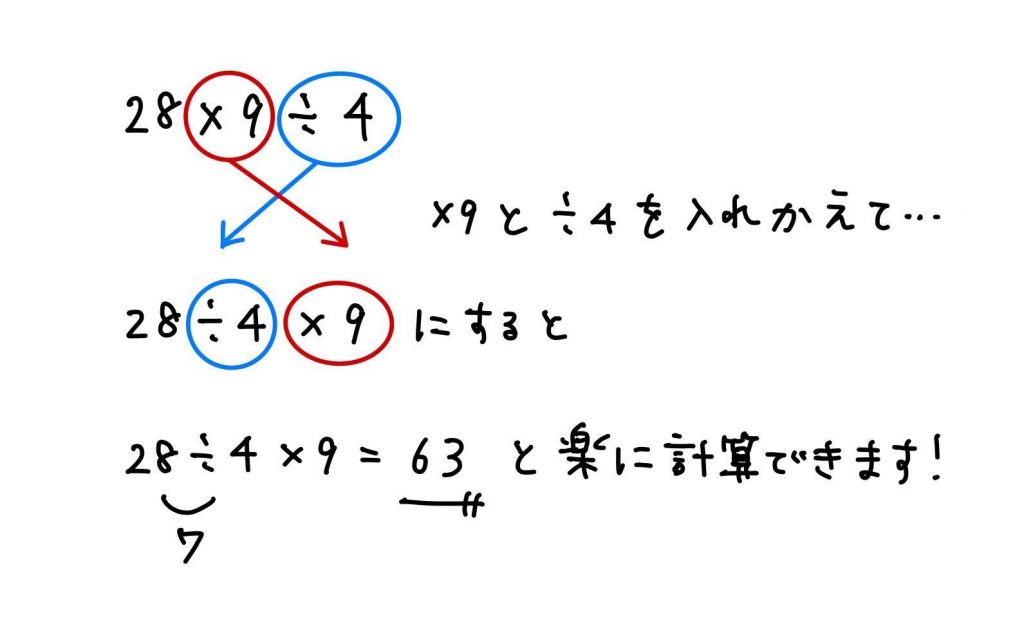
×9と÷4を入れ替えることで、計算が楽になりましたね。

×9と÷4を入れ替えても大丈夫なのは、わり算は逆数のかけ算に直すことができるからです

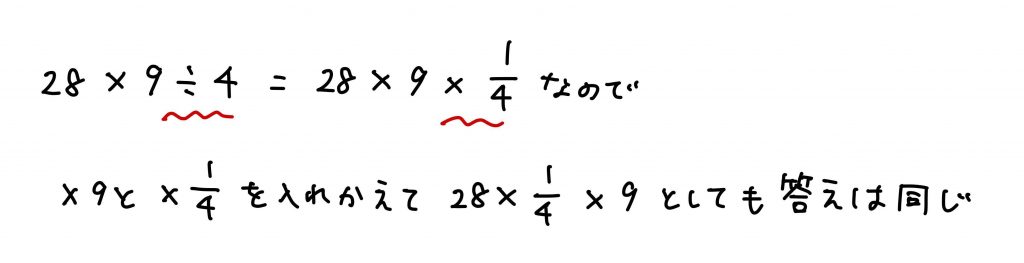
それでは練習問題です！

「順序を変える」を利用して、以下の問題を解いてみてください。

解答・解説は以下の通りです。

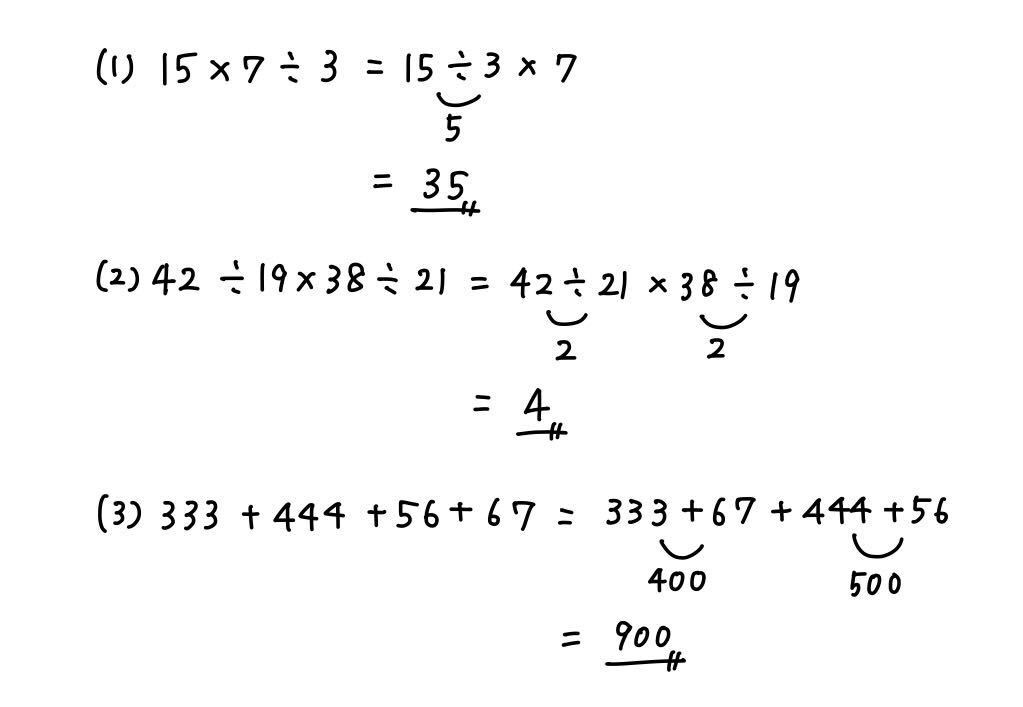
3．10,100,1000を作ろう

最後の工夫は「10,100,1000を作る」です！

まずは以下の計算をやってみましょう。

筆算でやろうとした子、ちょっと待った！

5×2＝10を利用して計算すると、以下のようになります。

10の倍数を作ることで、計算がより簡単になりましたね。

また、

• 25×4＝100
• 125×8＝1000

なども計算を楽にするのに使えます。

これらを踏まえて、練習問題を解いてみましょう！

答えはこちらです。

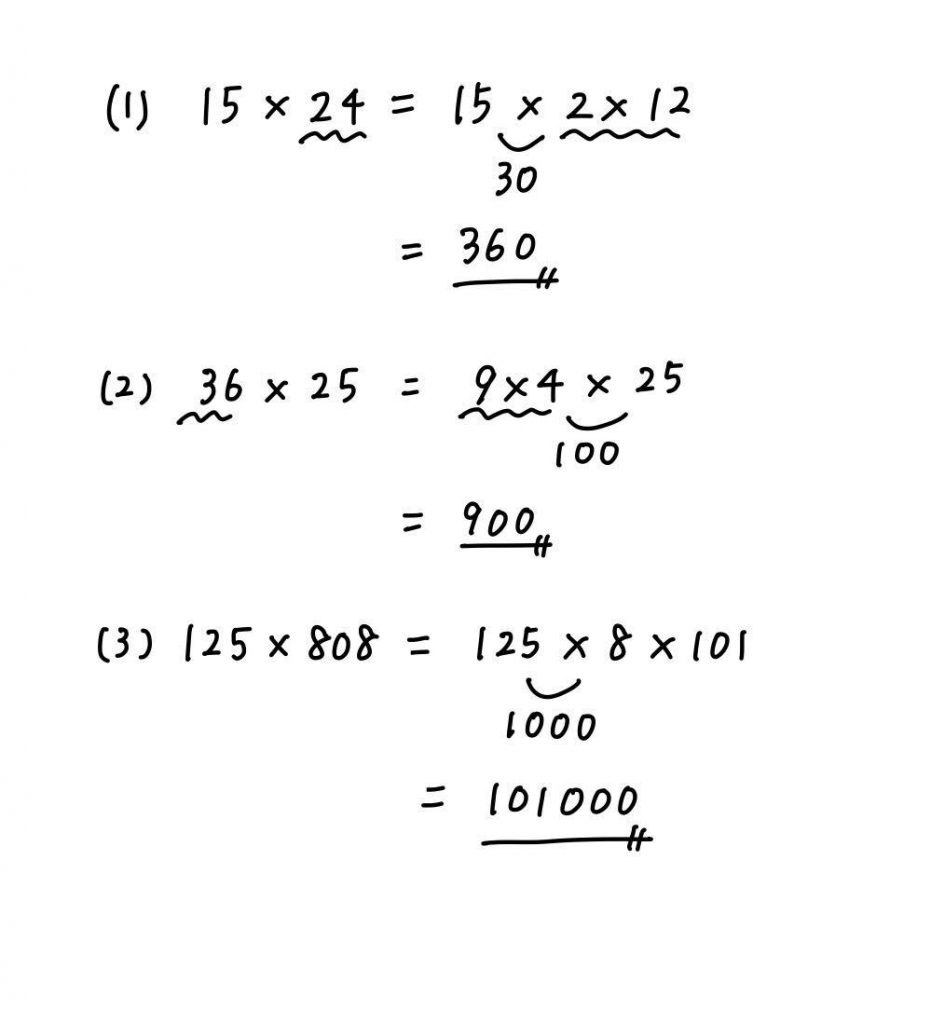
まとめ

1. 共通の数字でまとめよう
2. 順序を変えよう
3. 10,100,1000を作ろう

の3つの工夫を紹介しましたが、いかがだったでしょうか？

慣れないうちは「普通に計算する方が速いのに…」と思うこともあるかもしれませんが、使い慣れればお子さまにとって大きな武器＆一生の財産になります。

やり方や仕組みが理解できたら、あとは練習あるのみ。

実際に使ってみることで、自分のものにしていきましょう！

※記事の内容は執筆時点のものです