「扇形の面積が苦手」を克服する方法

平面図形の中でも、扇形に対して苦手意識を持っている子供は少なくありません。しかも、入試では扇形の面積や弧の長さについて単体で問われることはあまりなく、正方形と組み合わせた求積問題や、円錐の展開図など、複合的に問われることがほとんどです。

当然扇形に対して苦手意識を持っていると、このような入試問題には対応できません。扇形に対する苦手意識をなくすため、まずは基本的な公式の意味から理解していきましょう！

扇形は「円」と「割合」を用いて理解しよう

当たり前すぎてあまり意識することはないかもしれませんが、扇形とは「円から半径2本で切り取られた図形」です。

ここで重要なのは、扇形には「切り取られる前の円がある」ということです。つまり扇形は、元の円と切り取る割合によって決まります。これは言い換えれば、扇形の面積や弧の長さを考える際に重要なのは「円」と「割合」、この2つの単元の理解だということです。

扇形は円の一部

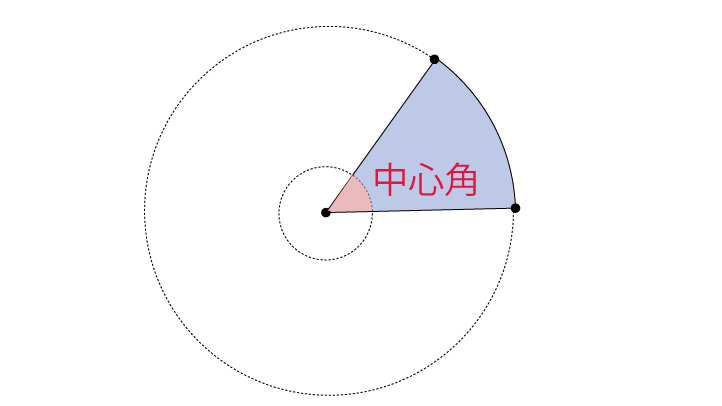
図のように扇形が円の一部であることを意識しましょう。そうすれば円の面積に、「円のなかで扇形の占める割合」をかければ扇形の面積が求められることがわかると思います。扇形の弧の長さも同様ですね。

式に直せば、

ということになります。

ここで、\(\frac{（中心角）}{360°}\) を「円のなかで扇形の占める割合」と定めれば、

で求められることになります。

これがいわゆる扇形の公式ですね。丸暗記ではなく、なぜこの公式で表せるのかを理解することは大切です。

扇形の占める「割合」が重要

単に公式として理解すると、あたかも扇形の面積や弧の長さを求めるために、「中心角を求める」のが必須なように見えます。しかし、角度を求めることにとらわれすぎる必要はありません。これまで書いてきた通り、重要なのは「割合」です。

これがわかっていれば、中心角を求めなくてもよい場合があり、無駄な計算を減らすことができます。

扇形の占める割合は弧の長さでも求められる

中心角なしで求める場合を考えてみましょう。

であるということは、

で求められるということですね。これを利用すれば、中心角なしで、扇形の面積や弧の長さを求めることができます。

実際に応用してみよう！

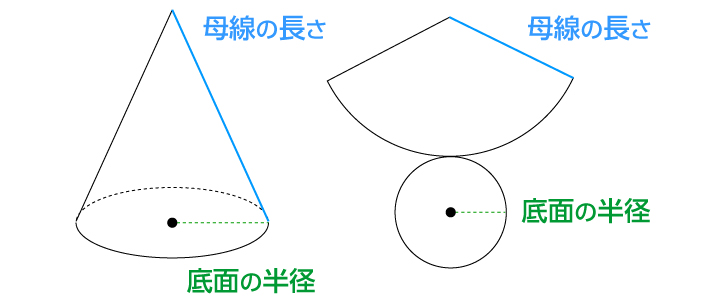
例えば、円錐の側面積を求める計算をしてみましょう。

底面の半径と、母線の長さがわかっていれば中心角なしで求められます。

展開図の扇形の弧の長さは、底面の円周と同じなので、

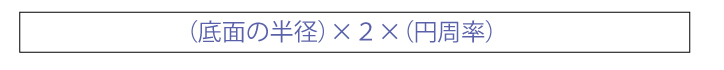
となります。

扇形の占める割合は、\(\frac{（扇形の弧の長さ）}{（円周）}\) なので式にすると

つまり、

ということになります。

この式を使って、円錐の側面積を求めると

と表すことができ、中心角なしで側面積を求めることができました。

基礎となる単元をしっかり理解しよう

公式を暗記して切り取ってしまうとわかりにくい応用も、体系的に学べば自然に受け入れられます。扇形の面積でいえば、円と割合の単元の理解が重要です。遠回りなようですが、ほかの単元から理解することで、本当の応用力が身につけられるのです。

※記事の内容は執筆時点のものです