旅人算ってどんなもの？ 旅人算をわかりやすく解説

「速さ」を使った文章題のひとつが旅人算です。旅人算にはパターンが複数あるため、どれが出題されても対応できるよう、準備しておく必要があります。速さの問題を不得意とするお子さんは多いので、しっかりと理解して、周りの受験生に差をつけましょう。

旅人算とは――中学受験ではどんな扱い？

旅人算とは、「速さ」の単元の問題の一種で、複数の人がでてきます。さまざまなバリエーションがあるのが特徴で、「駅にむかった母親を、自転車で追いかける」「池の周りを逆向きに走って出会う」といった問題が出題されます。

かなり複雑な問題もあり、特に難関校を受けるお子さんは対策が必須です。旅人算は速さの計算が身についていないと解けないので、あらかじめ、「速さ」「時間」「距離」を自由に使いこなせるようにしておきましょう。

旅人算の基本的な解き方

旅人算の基本的なパターンは「向かい合わせで出発する」パターンと、「追いかける」パターンです。それぞれの解き方を解説します。

旅人算の基本パターン1――向かい合わせで出発

まずは、状況を図にします。

【図1】

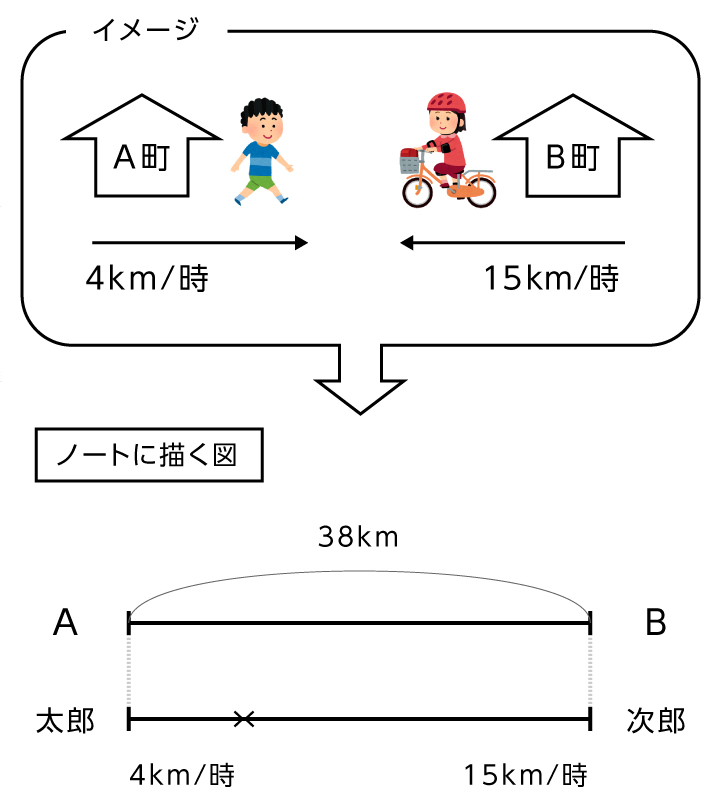
太郎君は1時間に4km、花子さんは1時間に15km進むので、2人合わせて1時間に

4＋15＝19km

進みます。

2人合わせて38kmの道のりを進めばよいので、かかる時間は

38（km）÷19（km/時）＝2時間

となります。

旅人算の基本パターン2――追いかける

状況を図にします。

【図2】

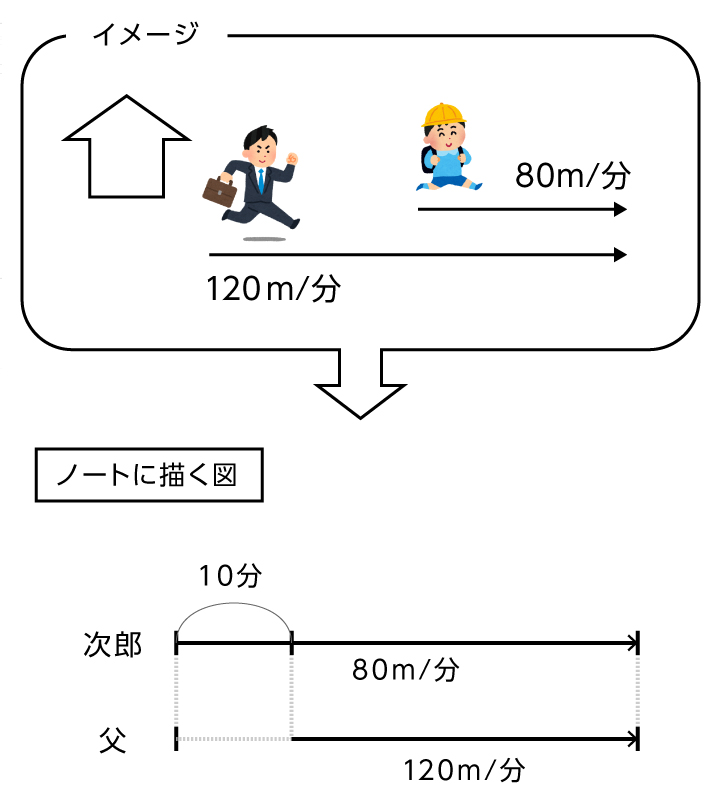
次郎君が出発してからお父さんが忘れ物に気づくまで、次郎君は

80（m/分）×10（分）＝800m

進んでいます。

お父さんと次郎君の速さの差は

120（m/分）－80（m/分）＝40（m/分）

です。

800mの距離を、40m/分で近づいていくので、

800（m）÷40（m/分）＝20（分）

午前7時10分にお父さんは家を出発しているので、

午前7時10分＋20分＝午前7時30分

に2人は出会います。

旅人算の問題には、2人が「池の周りを回る」などの形もあります。しかし、何かの周囲を回る問題も、ここで紹介した2パターンが基本です。まずは、「向かい合う」「追いかける」という2つの基本をおさえましょう。

旅人算で子供がつまずきやすいポイントとその対策

旅人算で子供がつまずきやすいポイントは、大きく分けて3つあります。

それぞれの対策を見ていきましょう。

［1］図が描けない

旅人算を解くうえで、図を描くことは非常にとても重要です。図を描かないと、状況が理解できないからです。

まずは【図1】【図2】の「イメージ」のような絵で、何が起きているのかを想像させましょう。そこから図を描くトレーニングをします。

図の描き方もパターンがあります。繰り返し解いていくうちに、「このパターンは、この図だな」とわかるようになります。

［2］処理方法がわからない

「図は描けているのに、その後の処理がわからない」といった場合、そもそも図の意味が理解できていないことがあります。もう一度、和差算にさかのぼって、図を使った解き方を復習しましょう。

また、旅人算はそもそも速さの計算がスムーズにできないと、図を描いても処理できないことがあります。お子さんが速さの計算でつまずいている場合は、そちらを優先的にフォローしましょう。

［3］応用問題に対処できない

旅人算の応用問題は、はっきり言って難しいです。ここで紹介した基本的な解法では解けず、比を使わなければ解けない問題もあります。しかし、まずはここで紹介した基本的な問題を解けるようにしましょう。応用問題の解法を覚えるのは、次の段階です。

旅人算は中学受験算数のなかでもかなりの難関です。速さの計算や、図を使った解き方を身につけることが重要です。基礎的な問題に取り組みながら、少しずつ難度を上げて会得していきましょう。いきなり難しい問題に飛びつかないのが、旅人算マスターのコツです。

※記事の内容は執筆時点のものです