正方形の対角線の長さを求めたい！ 小学生が算数の知識を使ってどこまでできる？

多角形で、隣り合わない2つの頂点を結んだ線を「対角線」といいます。多角形の中でも、正方形の対角線の長さは小学校の算数の範囲内で求めることができそうに思えますが……。実際のところはどうなのでしょうか？

今回は、正方形の対角線について考えてみたいと思います。

正方形の対角線の長さを求める方法はあるの？

まずは、次の問題を考えてみましょう。

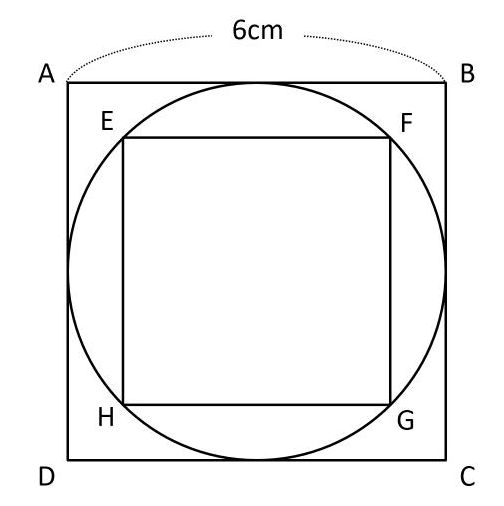
「長さを求めましょう」という問題が出るということは、小学生でも対角線EGの長さを求められるはずです。

円にくっついている正方形を45°回転させると……

正方形EFGHを45°回転させると、次の図のようになります。

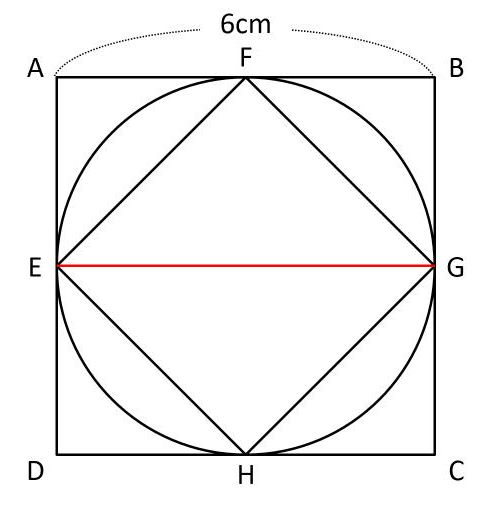
これを見れば、対角線EGの長さがABの長さに等しいことがわかります。したがって、EGの長さは6cmです。

この問題は発想の転換を必要とするパズル的な問題です。そのため、この問題を解くための考え方を他の正方形の対角線の長さを求めるのに応用することはできません。

では、一辺の長さが6cmの正方形ABCDの対角線ACの長さを求めることはできるでしょうか？

正方形の一辺の長さがわかっていても、対角線の長さを求められない

正方形の面積を求める公式は「面積＝一辺×一辺」です。また、正方形はひし形の一種なので、ひし形の面積公式「面積＝対角線×対角線÷2」も使えます。そこで、一辺の長さが6cmの正方形ABCDの面積を、2種類の公式を使って表してみます。

まずは、「面積＝一辺×一辺」より、面積は6×6＝36（cm²）です。次に、正方形ABCDの対角線ACの長さを□cmとして、「面積＝対角線×対角線÷2」より、面積は□×□÷2です。これが先に求めた面積の36（cm²）に等しいので、□×□÷2＝36となり、両辺に2をかけて□×□＝72となります。

小学生の算数の範囲では、この式の□の値を求めることができません。なぜなら、72は4（＝2×2）や64（＝8×8）のような平方数ではないからです。□の値を求めるには、中学数学で習う根号（√）の知識が必要になります。