倍数とはどのような数ですか？ 用語の区別と最小公倍数の求め方に慣れよう

中学受験算数では、「倍数」の理解がとても大切です。しかし、この倍数は、日常生活であまり使わない考え方なので、苦手とする受験生もちらほら……。さらには、「倍数」「公倍数」「最小公倍数」と紛らわしい言葉も出てくるので、「倍数が嫌い！」となってしまうこともあります。

そこで今回は、用語の確認や最小公倍数の求め方、倍数の問題の解き方を紹介します。

「倍数」「公倍数」「最小公倍数」を理解しよう

3の整数をかけていくと、3、6、9、12、15、……となっていきます。これらの数は、3×1、3×2、3×3、3×4、3×5、……となっていて、「3×整数」で表せます。このように、ある数を整数倍した数を倍数といいます。「Aの倍数」は「A×整数」という意味でもあります。

公倍数とは何ですか？

2の倍数と3の倍数を書き並べてみます。

2の倍数と3の倍数を見比べると、6と12が共通です。このように、複数の数に共通する倍数を公倍数といいます。

「公」は「共通の」という意味です。また、最も小さい公倍数を最小公倍数といいます。2と3の最小公倍数は6です。

公倍数は最小公倍数の倍数です。したがって、2と3の公倍数は、最小公倍数6の倍数である6、12、18、24、30、……です。

2つの数の最小公倍数を求めよう

公倍数を求めるには、最小公倍数を求めればよいことがわかりました。では、その最小公倍数は、どのようにすれば求められるのでしょうか？

2と3、4と5のように、2つ以上の数すべてを割り切れる数が1だけの場合、これらの数を「互いに素（そ）」といいます。

互いに素の数同士では、それらの数をかけた数が最小公倍数になります。たとえば、2と3の最小公倍数は2×3＝6、4と5の最小公倍数は4×5＝20です。

一方、互いに素でない数同士では、連除法（すだれ算）を用いて最小公倍数を求めると簡単です。連除法は次の手順で行います。今回は8と12の最小公倍数を求めます。

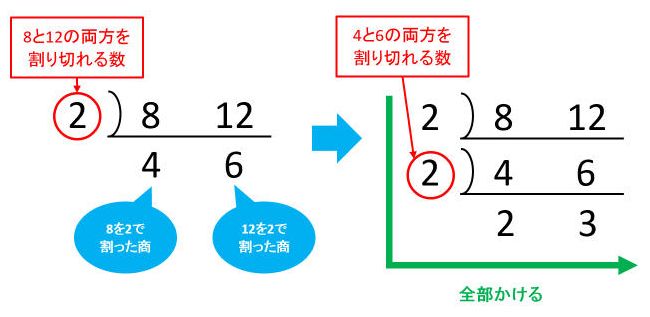
2つの数をどんどん割っていって、割り切れなくなったところで終了です。左の数と下の数をすべてかければ最小公倍数になります。8と12の最小公倍数は2×2×2×3＝24です。