方陣算がおもしろい！ 正方形の形に並べた碁石の数を上手に数えてみよう

「方陣」という言葉をご存知ですか？ 算数に登場する方陣として有名なのは「魔方陣」でしょう。魔方陣とは、数字を縦と横に同じ数だけ並べて、横・縦・斜めの和がすべて等しくなるようにした問題をいいます。中学受験算数でも魔方陣を時々見かけます。

しかし、それよりも出題頻度が高いのは「方陣算」です。方陣算は、正方形の形に並べた碁石の数を数える問題です。今回は、この方陣算について解説します。

中実方陣と中空方陣の考え方を理解しよう

方陣算には、碁石が中までぎっしりつまった中実方陣と、中の碁石が取り除かれている中空方陣の2種類があります。

それぞれの方陣算について、どのように考えればいいのでしょうか？

中実方陣のすべての碁石の数は平方数になる

碁石が中までぎっしりつまった中実方陣では、（縦の碁石の数）×（横の碁石の数）＝（すべての碁石の数）になります。ここで（縦の碁石の数）＝（横の碁石の数）なので、（すべての碁石の数）は1、4、9、16、…という平方数になります。このことをふまえて、次の問題を解いてみましょう。

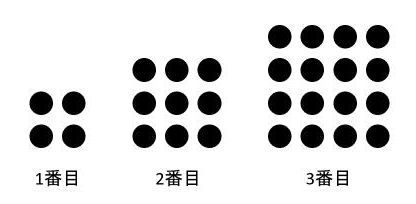
「あるきまり」がどのようなものかを考えます。1番目に並んでいる碁石は全部で4個です。同じように、2番目は9個、3番目は16個です。このことから、n番目に並んでいる碁石の数は全部で（n＋1）×（n＋1）で表されることがわかります。したがって、10番目に並んでいる碁石の数は全部で11×11＝121（個）です。

すべての碁石の数を数えるだけなら簡単でした。一方、周りに並んでいる碁石の数を数える場合、中空方陣になるので、少しだけ難しくなります。中空方陣については、次で解説します。

中空方陣では4つの角に位置する碁石に注意する

中の碁石が取り除かれている中空方陣では、正方形の4つの角に位置する碁石をどうするかがポイントです。次の2つの考え方があります。

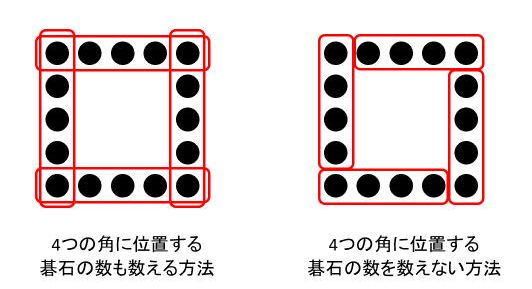
4つの角に位置する碁石の数も数える方法（上図：左）では、5×4＝20（個）を求めた後、4つの角に位置する碁石4個を引きます。したがって、20－4＝16（個）となります。