時間と速度の単位換算をわかりやすく解説
時間と速度の単位換算を苦手とする子は意外と多いです。その理由はおもに2つ。「解き方を知らない」「分数が苦手」です。時間と速度の問題が苦手な子は、この手の問題をみつけたとたん「自分には無理だな……」と考えて捨て問題にしてしまいます。点が取れる部分なのに、とてももったいないです。
今回は、親御さんがお子さんにわかりやすく教えられるよう、時間と速度の単位換算問題について解説していきます。
時間の単位換算
まずは解き方を覚えて自信をつけましょう。時間の単位換算は下記を覚えてしまえば簡単です。
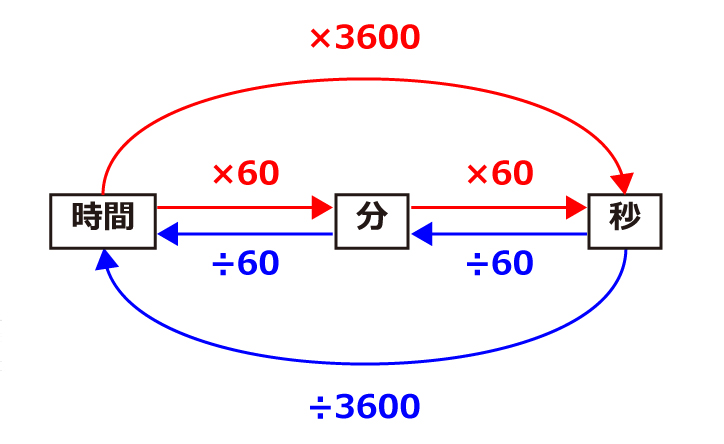
次の穴埋め式の例題を用いて解き方をみてきましょう。
24分は□時間です。
「分」を「時間」に直さなければいけないので、「÷60」します。
24÷60＝0.4
24分＝0.4時間 です。
分数をすでに学んでいるのであれば、次のように分数を利用して解く練習もしておくと、難問にも対応できるようになります。
\(\frac{24}{60}\)=\(\frac{2}{5}\)時間
理由を教える
解き方を覚えたら、なぜそうなのかを伝えることが重要です。
「時間」を「分」に換算する場合を考えてみましょう。
「1分が60回きたら1時間」なのですから、次のように表せます。
1時間＝60分
2時間＝60分×2＝120分
3時間＝60分×3＝180分
：
「時間」を「分」に換算する場合、「×60」ですね。
次に「分」を「時間」に換算するパターン。子供たちが問題でつまずきやすいのは、このパターンです。アナログ時計をケーキや円グラフに見立てて説明してあげると、イメージが湧きやすくなります。
1分は\(\frac{1}{60}\)時間
2分は\(\frac{2}{60}\)（＝\(\frac{1}{30}\)）時間
3分は\(\frac{3}{60}\)（＝\(\frac{1}{20}\)）時間
15分は\(\frac{15}{60}\)（＝\(\frac{1}{4}\)）時間
20分は\(\frac{20}{60}\)（＝\(\frac{1}{3}\)）時間
25分は\(\frac{25}{60}\)（＝\(\frac{5}{12}\)）時間
30分は\(\frac{30}{60}\)（＝\(\frac{1}{2}\)）時間
：
：
時計の盤面をよく見れば、1時間は60分に分けられることがわかります。
「分」を「時間」に換算するには、分母を60とする分数にするか、「÷60」の計算をするわけですね。
速度の単位換算
速度の単位換算も基本をおさえれば簡単です。まずは下記を覚えましょう。
前述した時間の単位換算とは「逆」なので要注意です。
では、次の例題を用いて解き方をみてきましょう。
時速12kmは分速□mです。
下の図のように、2つの単位に注目します。
「時速」から「分速」へ、「km」から「m」に換算しなければいけません。
「時速」から「分速」への換算は「÷60」ですから、
12÷60=0.2
で、時速0.2kmとなります。
次に、「km」から「m」への換算ですが、その前に「km」という単位に注目してみましょう。
「km」は下の図のように「接頭辞」と「基準の単位」でできています。
「k」（キロ）が「接頭辞」で「m」（メートル）が「基準の単位」です。
距離を表す単位は、ほかに「cm」（センチメートル）や「mm」（ミリメートル）がありますよね。それぞれの頭についている、「c」（センチ）と「m」（ミリ）は接頭辞です。
「k」（キロ）、「c」（センチ）、「m」（ミリ）といった接頭辞は基準の単位からどれくらい大きいか（or小さいか）を表すもので、代表的な接頭辞を表にすると次のようになります。
さて、「km」を「m」へ換算してみましょう。
換算は上の表を参考にするとわかりやすいです。
「k（キロ）」は基準の1000倍です。なので、1kmは1000mですね。
12÷60=0.2 ……「時速」から「分速」への換算
0.2×1000＝200 ……「km」から「m」への換算
これで、時速12kmは分速200mであることがわかりました。
前述の表の並びと小数点の移動で、次のように考えることもできます。
「k（キロ）」から基準へ行くには「どの方向」に「何回移動」しないといけないか考えます。この場合は「右に3回」移動が必要ですね。
ですから、0.2の小数点を「右に3回」移動させます。
この方法でも、分速0.2kmから分速200mへの変換ができました。
「ミリ」「センチ」「キロ」の換算も小学生がつまずきやすいポイントです。接頭辞と基準の単位をもとに換算する方法は、次の記事も参照ください。
・「ミリ」「センチ」「キロ」小学生が苦手な単位換算をわかりやすく解説
理由を教える
速度の換算も、なぜそうなのかを理解するのが重要です。難問を解くには、仕組みを理解する必要があります。まず速度とは何かを教えましょう。とても重要なポイントです。
「1時間」に進む距離を表したものが「時速」
「1分間」に進む距離を表したものが「分速」
「1秒間」に進む距離を表したものが「秒速」
つまり、先ほど例題で出てきた「時速12km」は「1時間に12km進む速さ」ということになります。1時間は60分ですから、言い換えると「60分に12km進む速さ」とできます。
ここまできたら、あと一息です。下記のように言葉を変えて表すことができませんか？
「時速12kmは分速□m」
「1時間に12km進む速さは、1分間に□m進む速さ」
「60分間に12km進む速さは、1分間に□m進む速さ」
かんの良い子供はこのあたりで納得し始めます。
「1分あたり何km進むかを考えて、そのあとkmをmに直せばいいんだ！」
ちなみに、線分図を使って考えると次のように表せます。
12÷60＝0.2km
0.2km=200m
やはり時速12kmは分速200mですね。
まとめ
苦手意識のある子供には、簡単な問題でやり方を教え、「自分には解けない」という意識から「解けるかも！」という意識へ誘導するのがおすすめです。その際「なぜそうなのか？」をゆっくりと教えましょう。この「なぜ？」を理解させることが、苦手を得意に変えるためのカギです。ぜひご家庭で試してみてください。
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます