時計算ってどんなもの？ 時計算をわかりやすく解説

時計算の問題はシンプルですが、計算の複雑さもあいまって、これを苦手とする子供も多いです。この記事では時計算がどういったものなのか、そして基本的な解き方と子供がつまずきやすいポイントを解説します。

時計算とは？ 中学受験ではどのような扱い？

時計算とは、時計の長針と短針が作る角度を使った問題です。入試では、長針と短針の作る角度を求める問題や、逆に角度から時間を求める問題などが出題されます。

時計の針の動きをイメージできなかったり、計算式を立てる作業が難しかったりするため、受験生には敬遠されがちです。

しかし、苦手といっても、入試には出題されます。時計算は簡単な計算問題のひとつや、中級レベルの問題として出題されることがほとんどなので、解けるようにしておきたい問題のひとつです。

時計算の基本的な解き方解説

次の例題をもとに時計算の基本的な解き方を見ていきましょう。

まずは、長針と短針 がそれぞれ1分間に何度進むかを考えます。

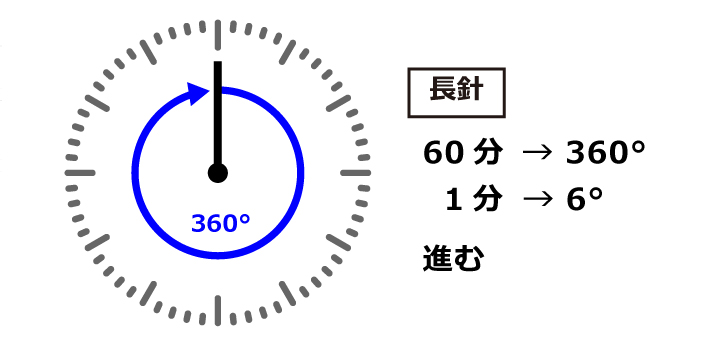
長針は1時間（60分）で360^°回るので、1分間に

360÷60＝6^°

進みます。

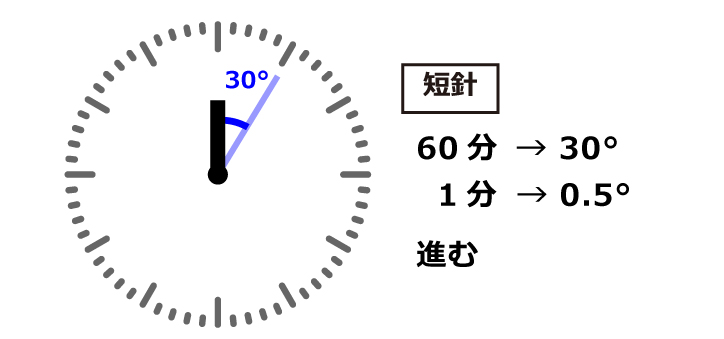
一方、短針は1時間（60分）で30^°進みます。よって、1分間では、

30÷60＝0.5^°

進みます。

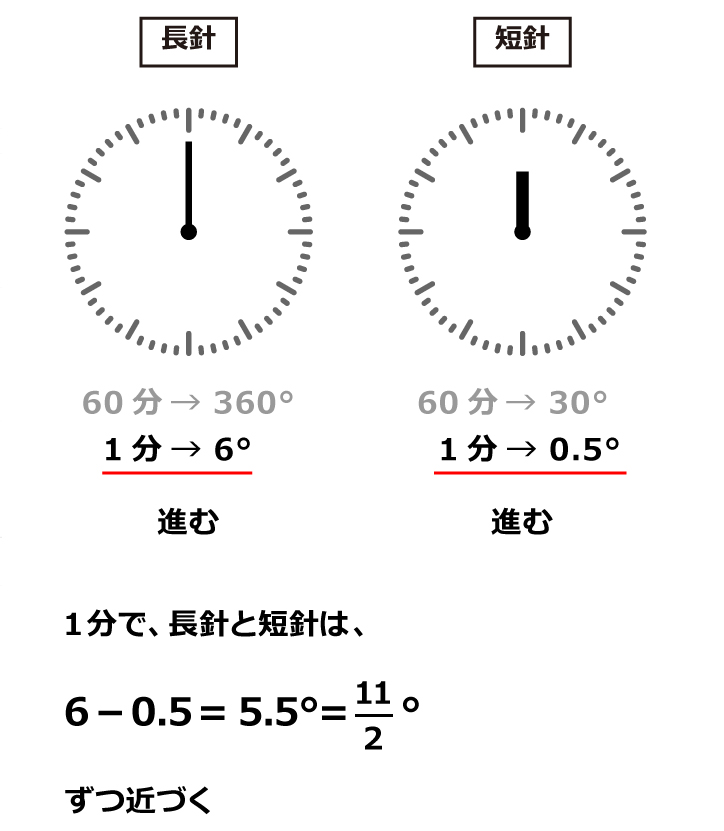
次に、1分間の長針と短針の動きを確認してみましょう。

長針も短針も同じ方向に進みます。

そこで、旅人算の要領で考えると、2つの針が作る角度は1分間に

6－0.5＝5.5^°＝\(\frac{11}{2}\)^°

ずつ小さく なっていくことがわかります。

ここまでが、時計算に必要な前提知識です。

前提知識を確認したところで、先ほどの問題に戻りましょう。

5時のときを図にすると、次のようになります。

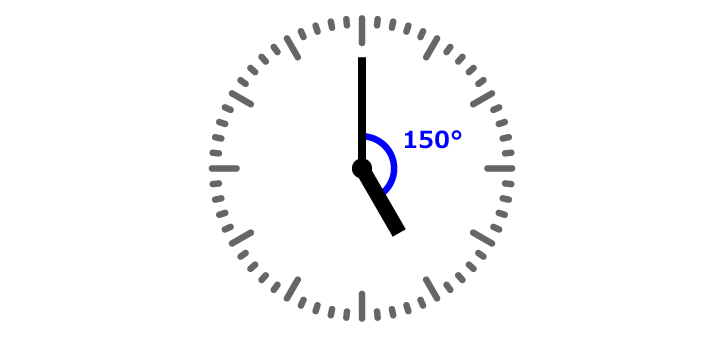
5時のとき、長針と短針が作る角度は150^°ですね。ここから、先ほど説明したとおり、短針と長針が作る角度は1分間に5.5^°（\(\frac{11}{2}\)^° ）ずつ小さくなっていきます。

よって、短針と長針が重なるのは

150÷5.5

＝150÷\(\frac{11}{2}\)＝150×\(\frac{2}{11}\)

＝27\(\frac{3}{11}\)分後

です。

「5時と6時の間で、長針と短針が重なる時間」なので、

5時27\(\frac{3}{11}\)分

が答えとなります。

時計算で子供がつまずきやすいポイント

子供がつまずきやすいポイントは、以下の3つです。

それぞれ対策を見ていきましょう。

［1］分数の計算ができない

「中学受験を考えている子が、5・6年生の段階で分数の計算ができないわけがない」と考えている親御さんは多いです。しかし、実際には高学年になっても分数の計算が怪しい子がいます。

特に時計算は「小数から分数に直す」「分母が11になり、なんだか気持ちが悪い」計算になりますので、今まで分数の計算ができていた子供もつまずくことはよくあります。

対策として、日々の学習で分数の計算を繰り返すとともに、時計算の場合は割り切れない数（多くの場合、分母が11）が答えになることが多い、ということを覚えておきましょう。

［2］長針と短針の作る角度が「1分間に5.5°小さくなる」ことがわからない

時計算は、円の周りを同じ方向に進む旅人算の考えを使います。そのため、「長針の進んだ角度－短針の進んだ角度＝5.5^°」という値が導き出せるのです。

この理屈を飛ばして、単に「5.5^°」という数字だけを覚えている子供がいますが、これはやめた方がよいでしょう。

時計の針の動きがわからないと、複雑な問題のとき、どうやって解けばよいのかわからなくなってしまうからです。必ず、「同じ方向に進むから、それぞれの進む角度の引き算をするんだ」という意識をもたせましょう。

［3］出題のパターンが変わると解けなくなる

旅人算にはいくつかの決まったパターンがあります。

ここでは一番基本的な「長針と短針が重なる」パターンの問題を取り上げましたが、ほかに

といった問題が出題されます。

こういった問題の場合、解法を知らないとなかなか自力で解くことはできませんが、まずは基本をおさえうえで、こういった問題の解法をおさえていくことが肝要です。

時計の針が進むイメージをもつ

ここでは簡単に説明するために「時計の針が近づく」「角度が小さくなる」と表現しましたが、正確には、時計の針には次の3つの状態（近づく、重なる、遠ざかる）があります。

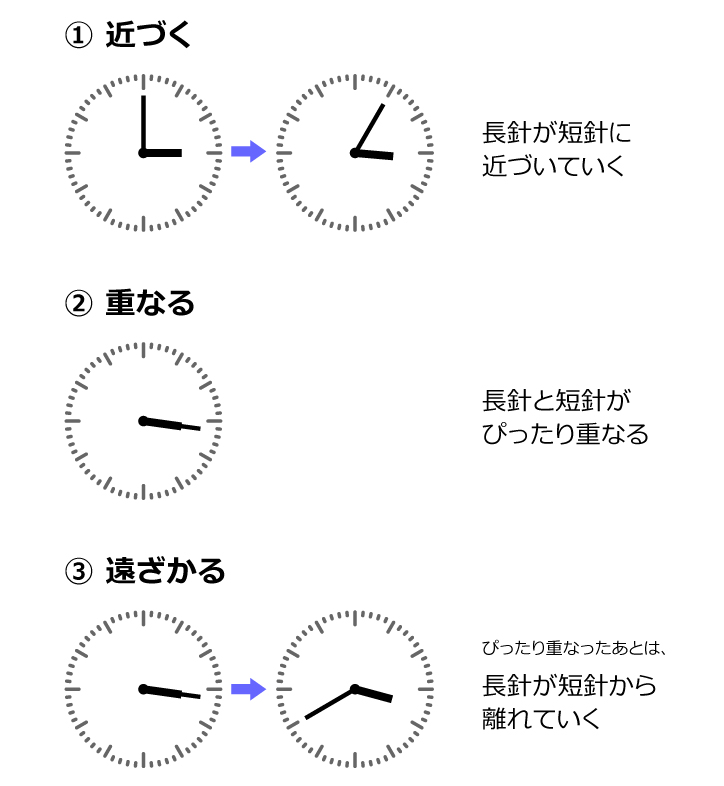
実際の時計を思い浮かべるとわかりやすいでしょう。上の図は3時からの針の動きです。長針が短針に近づき、2つの針が重なったあと、離れていきます。

時計算は針が進むイメージをもち、「今、長針と短針がどの状態にあり、どこの角度を問われているのか」を念頭において問題を解くことが重要です。

もっともこの部分は子供が混乱に陥りやすい部分でもあるので、まずは「長針と短針が近づくパターン」を確実に解けるようにしてから、ほかのパターンも解けるようにしていきましょう。

※記事の内容は執筆時点のものです