【サイコロの展開図】中学受験生が押さえておきたい3つの基礎知識

立体図形が苦手な子は多いかと思いますが、なかでも「展開図」がからむとさらにわからなくなってしまう子は少なくないでしょう。そこで展開図を苦手としている場合には、まずは展開図の基本ともいえる「立方体」をマスターすることがおすすめです。

この記事では、サイコロの展開図をベースに、展開図の問題を攻略するために押さえておきたい3つの基礎知識をお伝えします。後半では、基礎知識を使って解ける例題も紹介するので、ぜひ挑戦してみてくださいね。

3つの基礎知識

まずは、サイコロの展開図をマスターするために必要な「3つの基礎知識」から見ていきましょう。お伝えする知識をしっかり身につけることで、サイコロの展開図の“本質”を理解できるようになります。

基礎知識【1】サイコロは「対（つい）」で整理する

そもそもサイコロは、立方体です。そして立方体は6つの面を持った立体のことですが、このとき「2つの向かい合った面が3対（つい）ある立体」と考えておくと、展開図に関してもスッキリと理解できます。

なお3つの対を区別する場合には、日常生活でも馴染みのある次の言葉に置き換えてみるのがおすすめです。

この3つの対がどれかひとつでも異なっていると、面のパターンが違うサイコロになります。この3つの対は“超重要”なので、サイコロの展開図を見たときは、まずはしっかりと意識するようにしましょう。

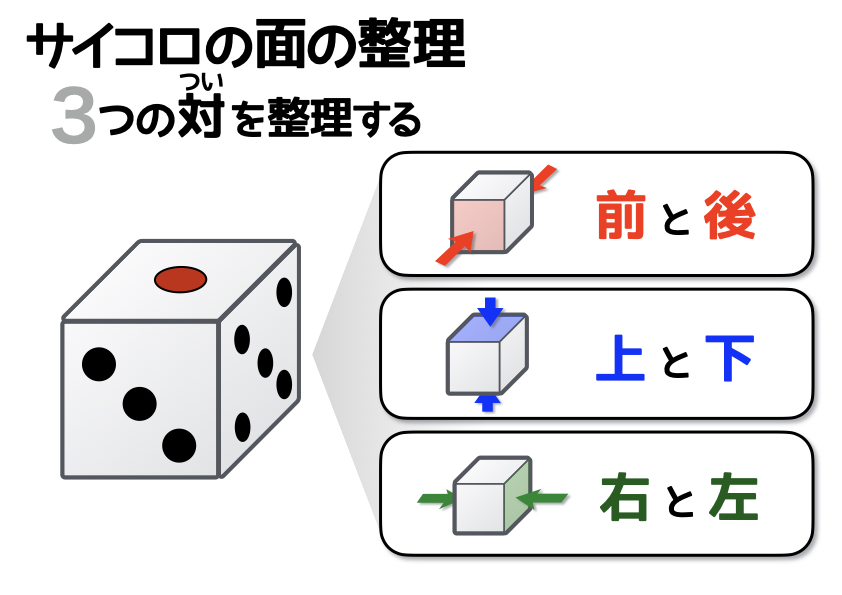
そしてもうひとつ重要なことは、「向かい合う面の目の合計は7」ということです。この知識は中学受験では覚えなくても大丈夫ですが、サイコロの展開図の問題では、ほぼ確実に問題文に記されています。ちなみに上の図では「前」が3となっているので、「後」の面は4になっていることがわかりますね。

基礎知識【2】展開図には4つのパターンがある

では、サイコロを展開していきます。ちなみに「展開図」と聞くと無数のパターンが存在すると思うかもしれませんが、実はたった4つのパターンに分類できてしまいます。

パターン【1】1つ／4つ／1つ

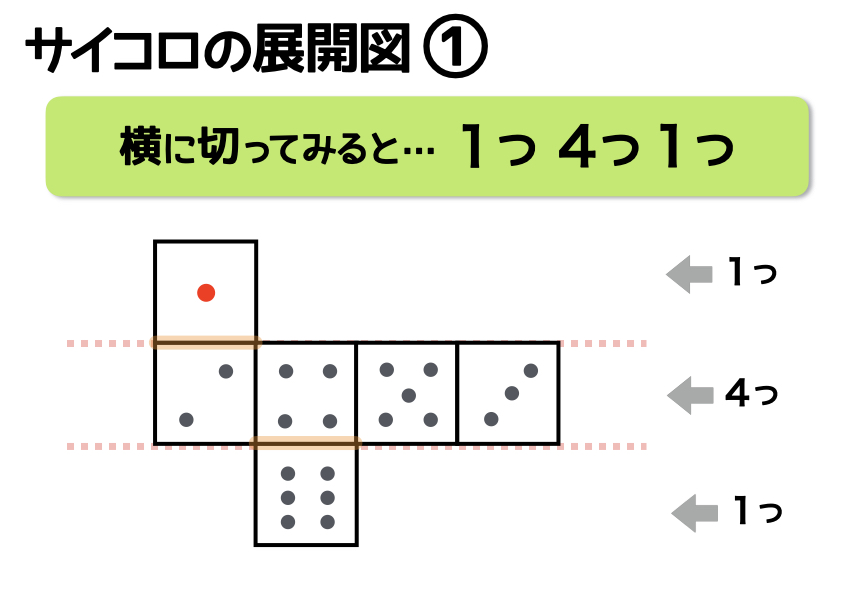
まずひとつ目は、展開図を横に切ってみたときに、上段に1つ、中段に4つ、下段に1つの正方形が合わさっているパタ―ンです。この展開図はメジャーなため、頭のなかでも組み立てやすい形といえるでしょう。

パターン【2】1つ／3つ／2つ

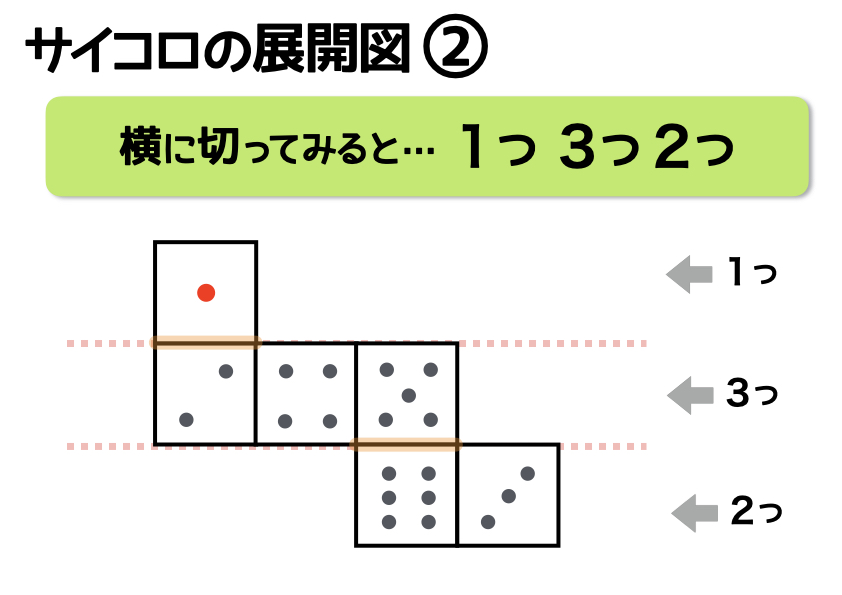
ふたつ目は、上段に1つ、中段に3つ、下段に2つの正方形が合わさっているパターンです。パターン1よりも、少しだけ複雑に感じるかもしれません。

パターン【3】2つ／2つ／2つ

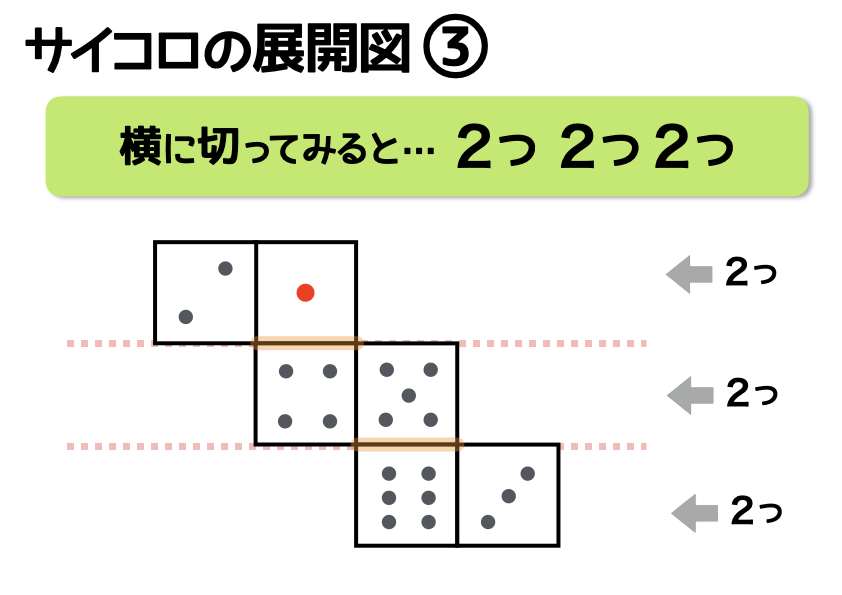
3つ目は、上段に2つ、中段に2つ、下段に2つの正方形が合わさっているパターンです。この形は、頭のなかだけで組み立てるのはちょっと難しそうです。

パターン【4】3つ／3つ

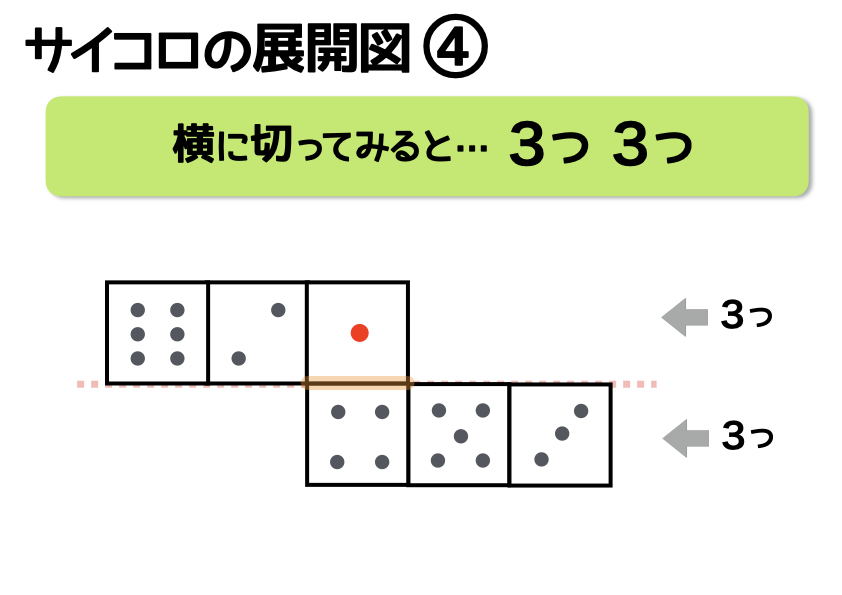
最後は、これまでと違って「2段」の展開図です。上の図をみると、上段3つ、下段3つとなっていますね。この展開図も、頭のなかで組み立てるのは苦労するかもしれません。

基礎知識【3】展開図では、対になる面は「隣の隣」になる

向かい合った3つの面でサイコロを整理すること、そして展開図のパターンを見てきました。そして、展開図でも「3つの対」が大切なカギをにぎります。具体的には、まずは展開図では対になる面が「隣の隣」にくることを押さえましょう。また、2つの対がわかると残りが決まる、という知識も合わせて覚えておきたいですね。