
【算数】歯車の問題は「表」で攻略しよう! 押さえておきたい基礎知識や例題も紹介
算数の単元「比例と反比例」で突然登場する、歯車の問題。歯車の歯数や、回転数の比や逆比を使った解き方が掲載されていることが多いですが、その解説がどうもわかりにくく、頭を抱えている子は多いかもしれません。筆者の子供も、教科書やテキストの解説を読んでもいまいちピンときていない様子で、比や逆比を使ってなんとか説明しても理解できず……。一方で、歯車の情報を「表」で整理する方法をすすめてみたところ、スッキリと理解できたようでした。
そこでこの記事でも、表を使って歯車の問題を解く方法をお伝えします。例題も紹介しますので、「比や逆比を使った解き方が理解できない……」と悩んでいる場合には、ぜひ最後まで読み進めてみてください。
Contents [hide]
3つの基礎知識
歯車を正しく理解するためには、そもそも歯車がどのような性質を持っているか知る必要があります。「性質」と聞くと難しく感じてしまうかもしれませんが、押さえるべきことは3つだけ。これらの知識を知っておくと、歯車の問題がグッと解きやすくなります。
3つの基礎知識
- 歯車の歯数×回転数=進む歯数
- 噛み合った歯車&軸が同じ歯車
- 歯車どうしの関係(重要ポイント!)
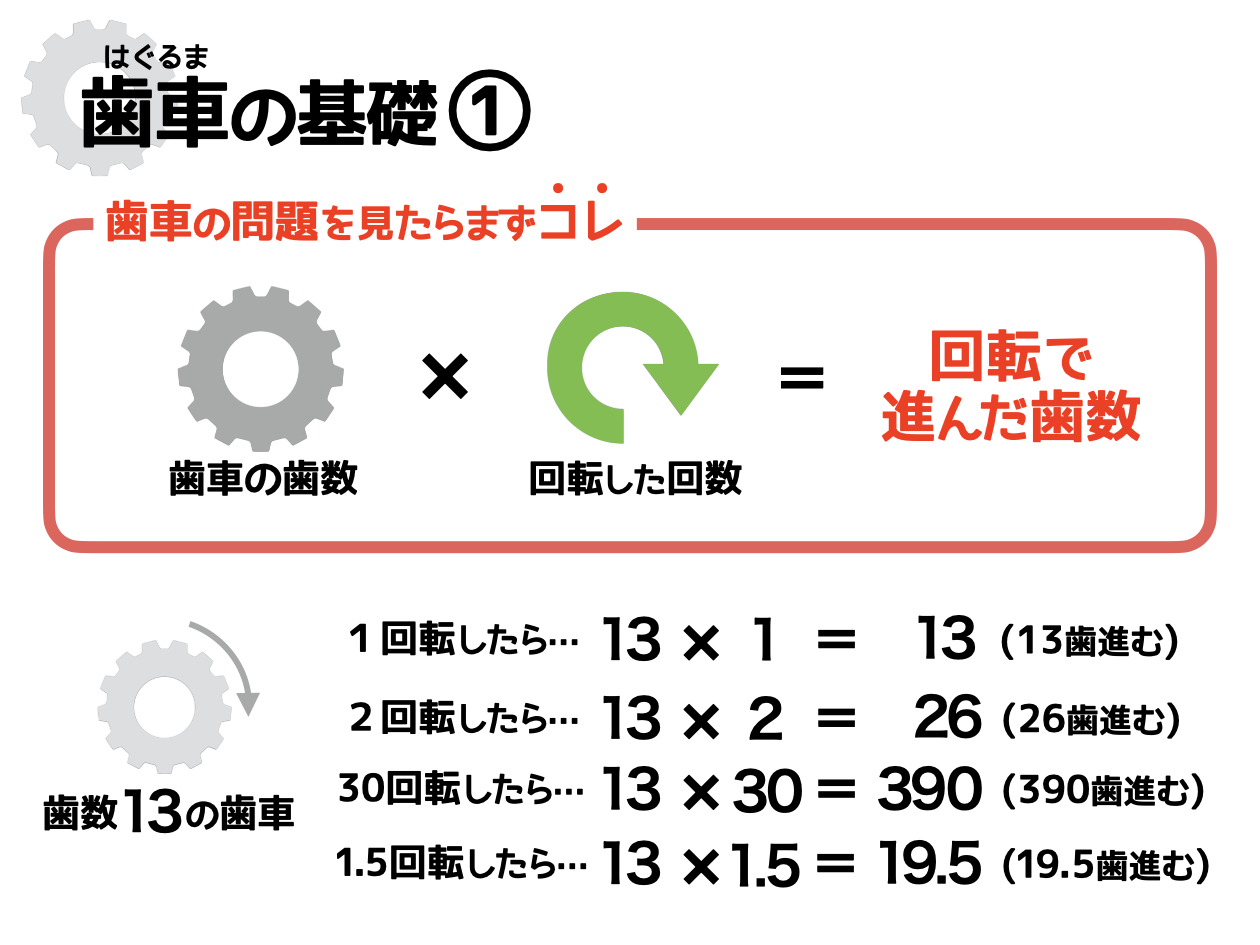
1、歯車の歯数×回転数=進む歯数
歯車の問題を見たら、まずは「3つの数を整理する」という意識をもちましょう。
意識したい3つの数
- 歯車の歯数
- 回転数
- 進む歯数
これらは問題にすべて書かれているとは限らず、遠回りな書き方をされている場合もありますが、いずれにせよ、この3つを押さえることは歯車の問題を解くうえで大切です。
たとえば歯の数が「13」の歯車が1回転すると、13歯進みますね。2回転なら26歯です。では、30回転ではどうでしょうか? または1.5回転ではどうなると思いますか? この場合も、考え方は変わりません。具体的には次のように計算します。
歯の数が13の場合
30回転:13×30=390(390歯進む)
1.5回転:13×1.5=19.5(19.5歯進む)
このように、歯車が回転することで進む数は「歯車の歯数」と「回転数」を掛けることで簡単に計算できます。
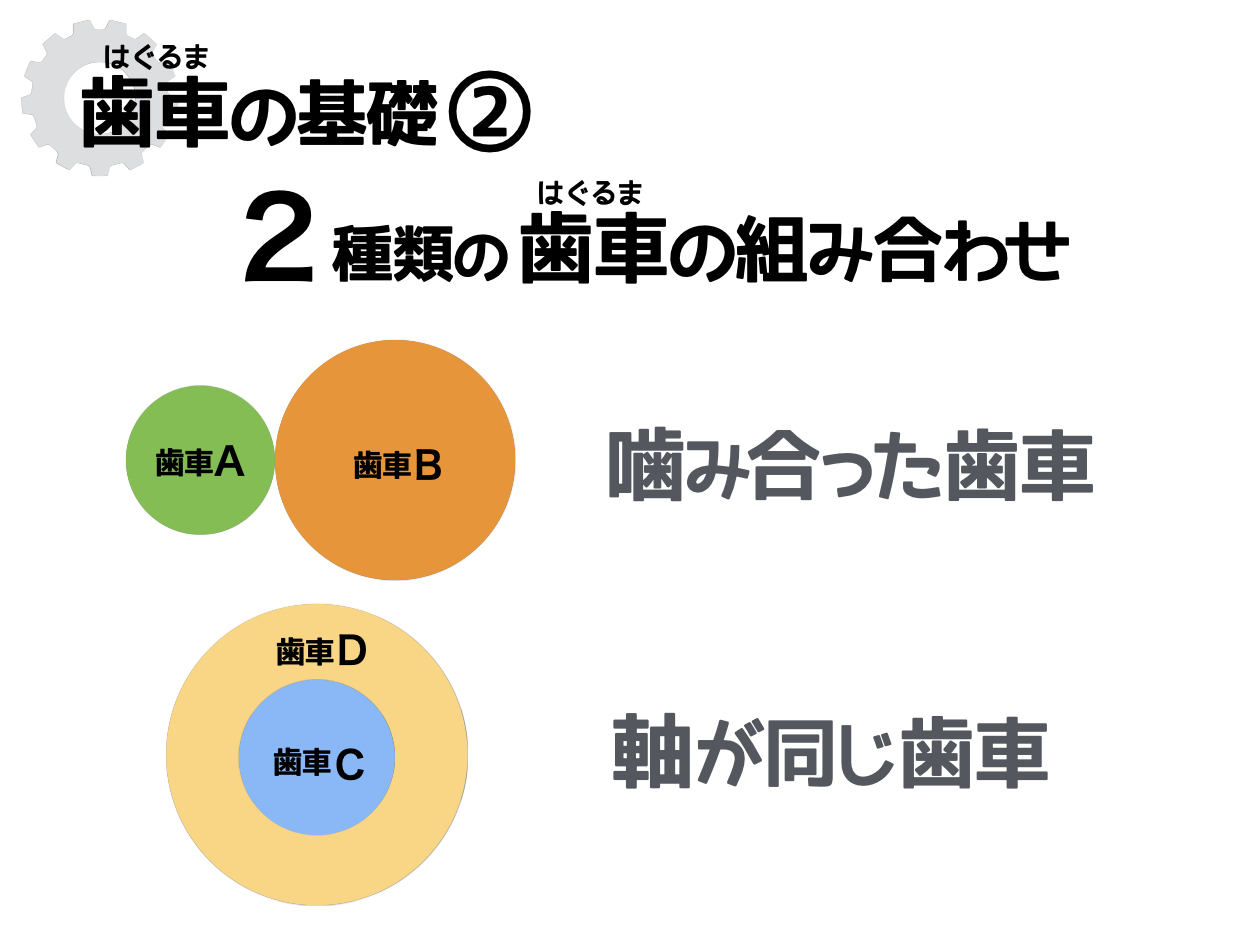
2、噛み合った歯車&軸が同じ歯車
歯車は単体で使われることはなく、ふたつ以上の歯車を組み合わせて使われるのが一般的です。そして実は、組み合わせ方には次の2種類が存在します。
歯車の組み合わせ方
- 噛み合った歯車
- 軸が同じ歯車
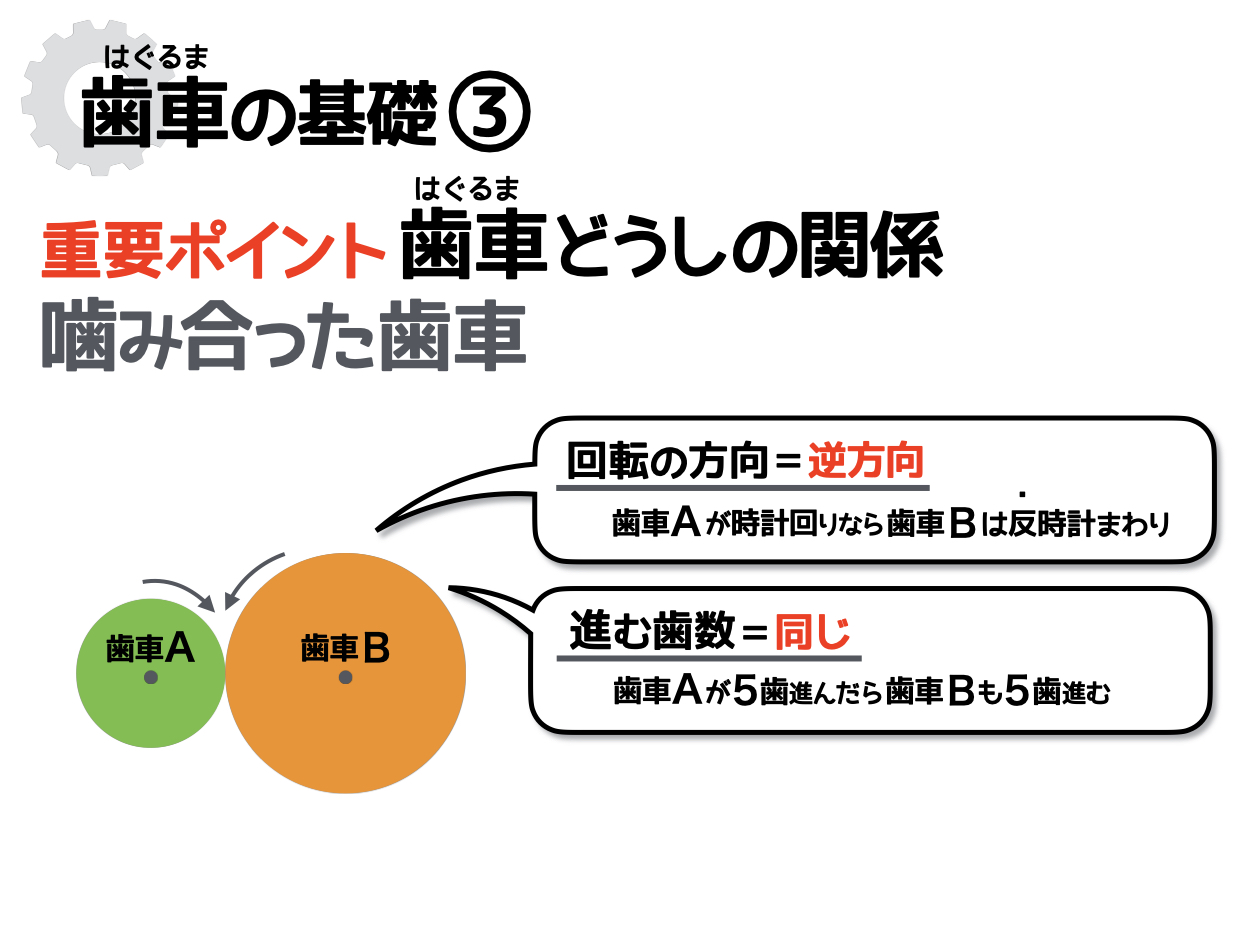
3、歯車どうしの関係(重要ポイント!)
「噛み合った歯車」が回転する様子をイメージしてみましょう。このとき、ふたつの歯車が進む歯数は同じです。そして、それぞれの歯車が回転する方向は逆になります。
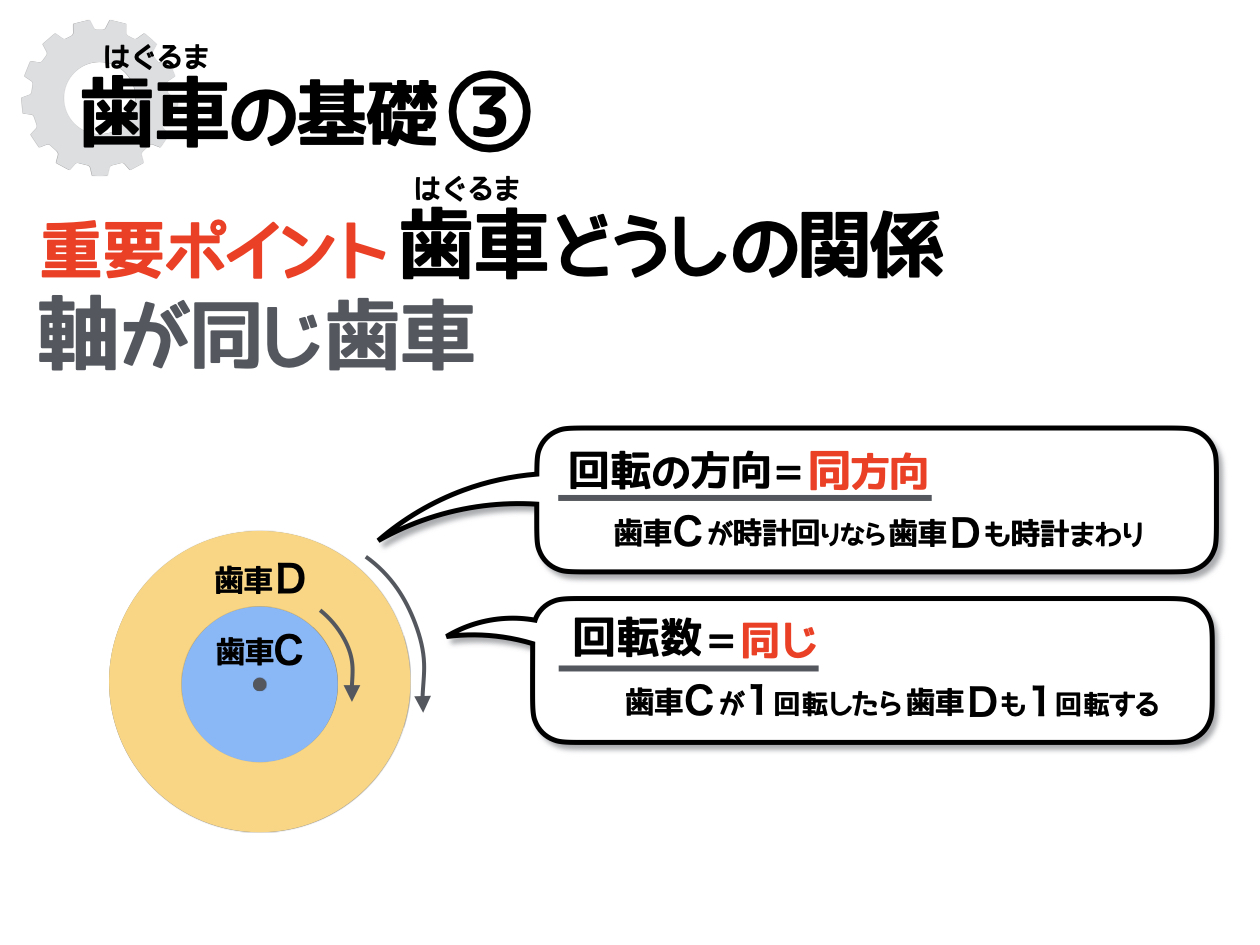
 次に、「軸が同じ歯車」が回転する様子を想像してみましょう。このとき、ふたつの歯車の回転数は同じで、さらには回転する方向も同じになりますね。
次に、「軸が同じ歯車」が回転する様子を想像してみましょう。このとき、ふたつの歯車の回転数は同じで、さらには回転する方向も同じになりますね。
ここまでの情報をまとめると、次のとおりです。大切な知識のため、しっかりと押さえておきましょう。
■噛み合った歯車
進む歯数は同じ、回転の方向は逆
■軸が同じ歯車
回転数は同じ、回転の方向も同じ
表を使った解き方
歯車の問題は、表を使うとシンプルに解くことができます。さっそく「サンプル問題」を使いつつ、答えを導いていきましょう。なお、解く際には次のステップを踏むのがおすすめです。
解き方の3ステップ
- 情報を整理する
- 歯車の関係性をもとに表を埋める
- 答えを導きだす
<サンプル問題>
歯数が30の歯車Aと、歯数が50の歯車Bが噛み合っています。歯車Aが時計回りに100回転した時に、歯車Bはどちらの方向に何回転するでしょうか?
ステップ[1]情報を整理する
はじめに、問題文の情報を整理しましょう。整理する情報は先ほどお伝えしましたが、思い出せますか? そう、次の3つでしたね。
- 歯車の歯数
- 回転数
- 進む歯数
歯車Aの「進む歯数」は示されていませんが、問題文から「歯車の歯数(30)」と「回転数(100回)」はわかっているので、掛け算によって求められます。

ステップ[2]歯車の関係性をもとに表を埋める
問題文から情報を整理できたら、いよいよ重要知識の出番。この問題のふたつの歯車は「噛み合った歯車」のため、進む歯数は同じで、回転の方向は逆です。この知識をもとに考えると、歯車Bの「進む歯数」の空欄が埋められます。そして「回転の方向」には“反時計回り”と記入できますね。
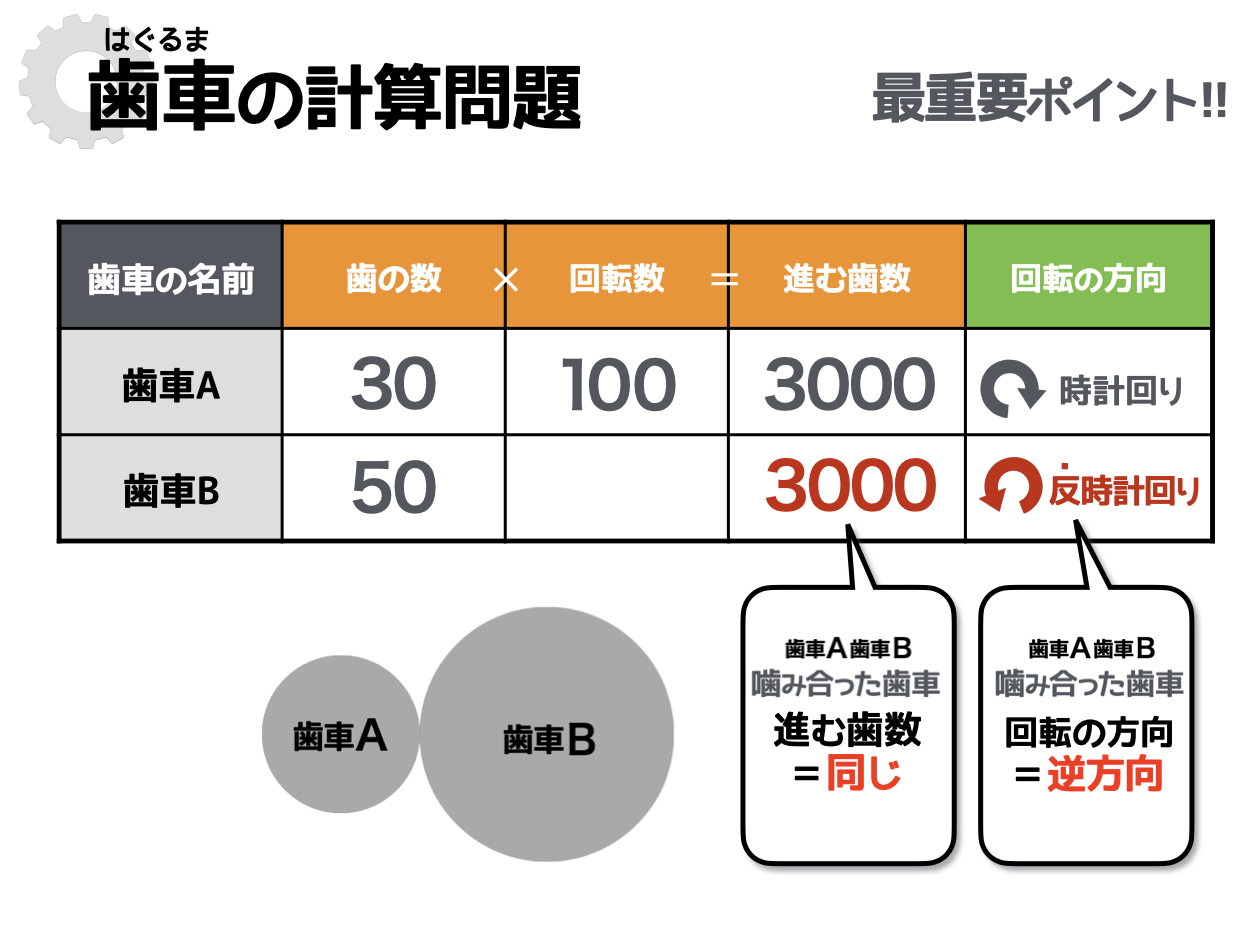
※図の縮尺は目安です
「ふたつの歯車の関係性をもとに表の数字を埋める」というステップは、歯車の問題では特に重要なポイントです。しっかりとマスターしましょう!
ステップ[3]答えを導きだす
基本的な情報を表にまとめ、歯車どうしの関係性をもとに表を埋めていけば、答えは表のなかに見えてきます。
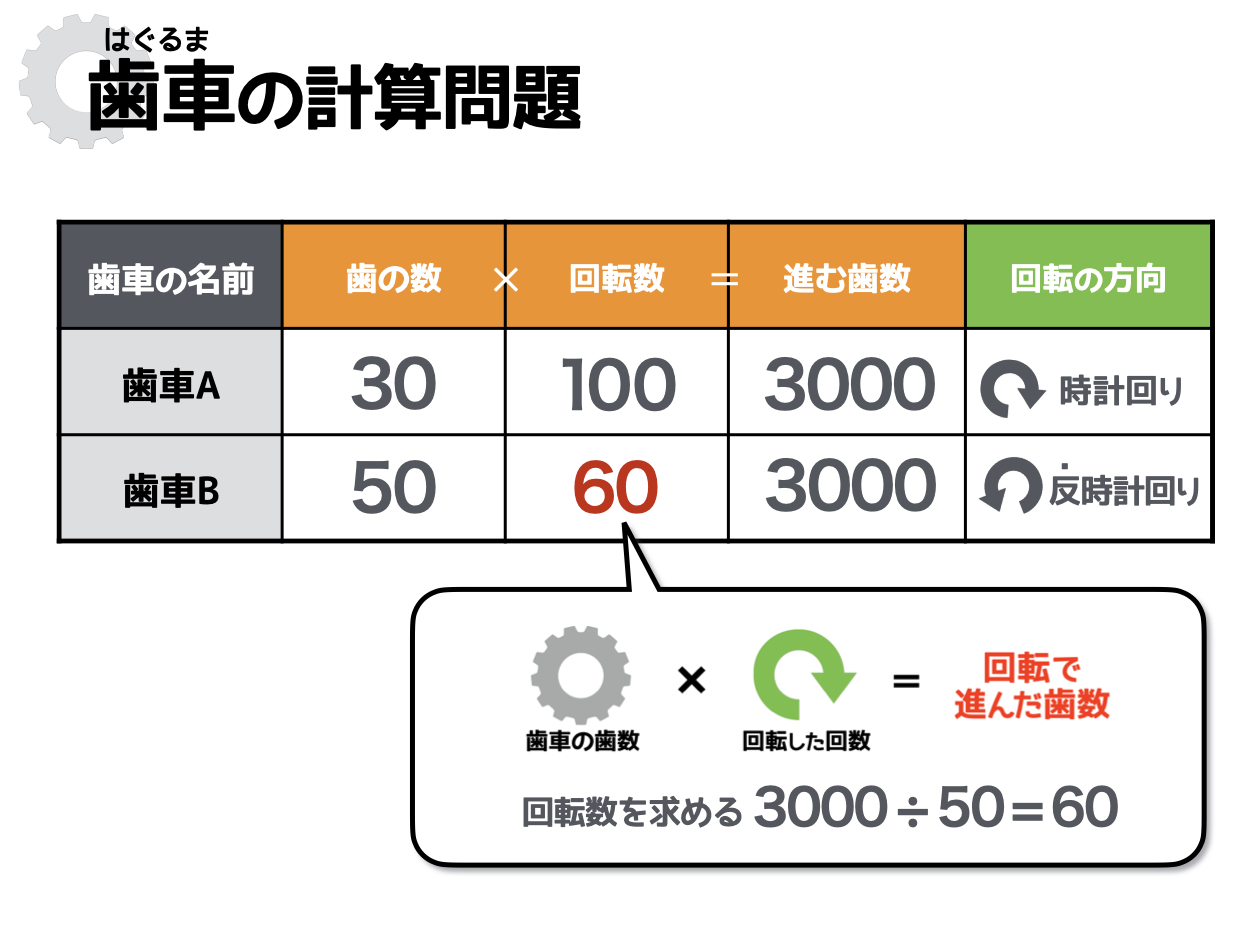
答えは、歯車Bは「反時計回りに60回転する」です。
例題で解き方をたしかめよう
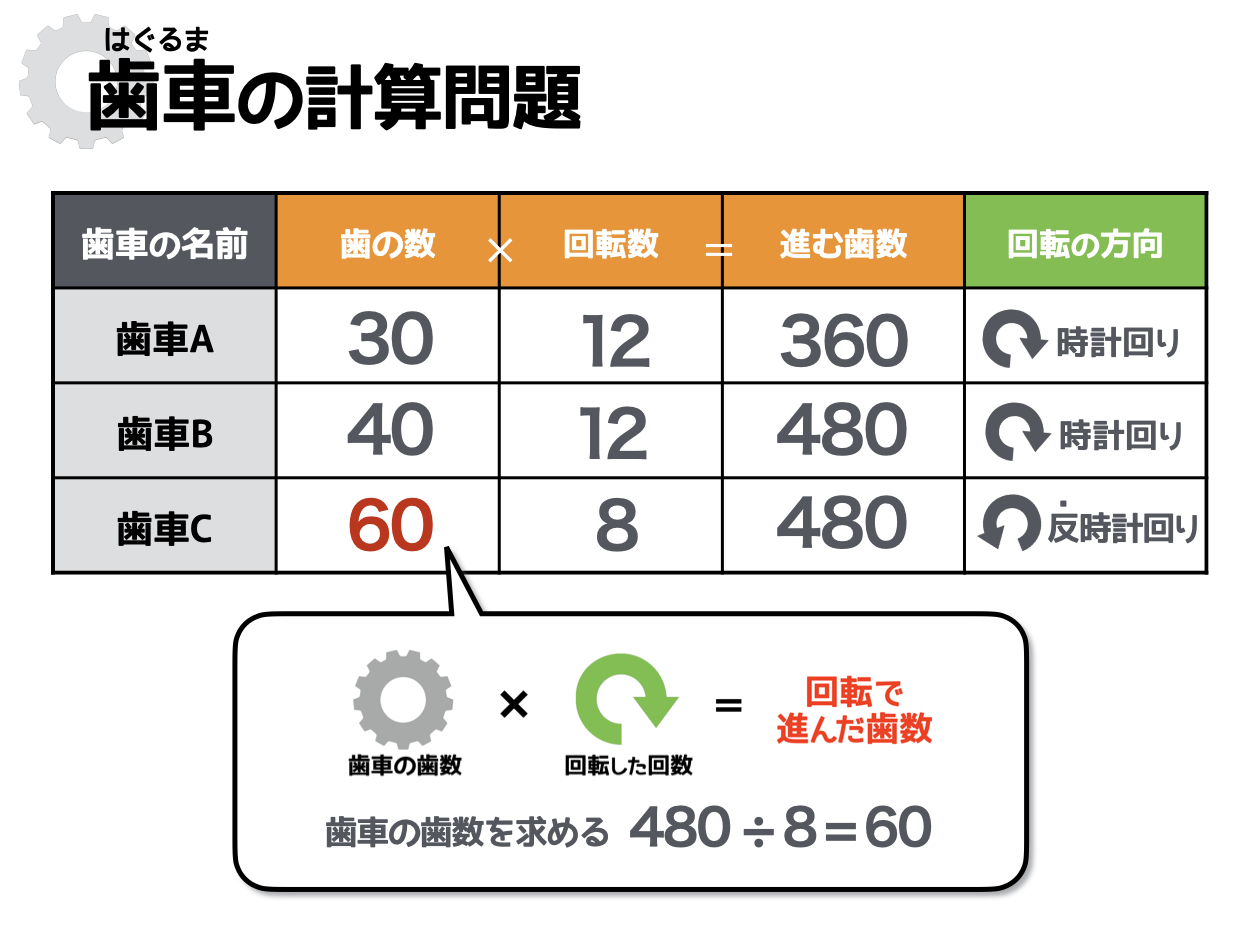
<例題>
歯数30の歯車Aと、歯数40の歯車Bと、歯車Cがあります。歯車Aと歯車Bの軸は同じで、歯車Bと歯車Cは噛み合っています。歯車Aが時計回りに12回転した時、歯車Cは8回転しました。歯車Cの歯数はいくつでしょう?
さっそく、問題文の情報をもとに表をつくりましょう。歯車が3つなので、表は3行になりますね。
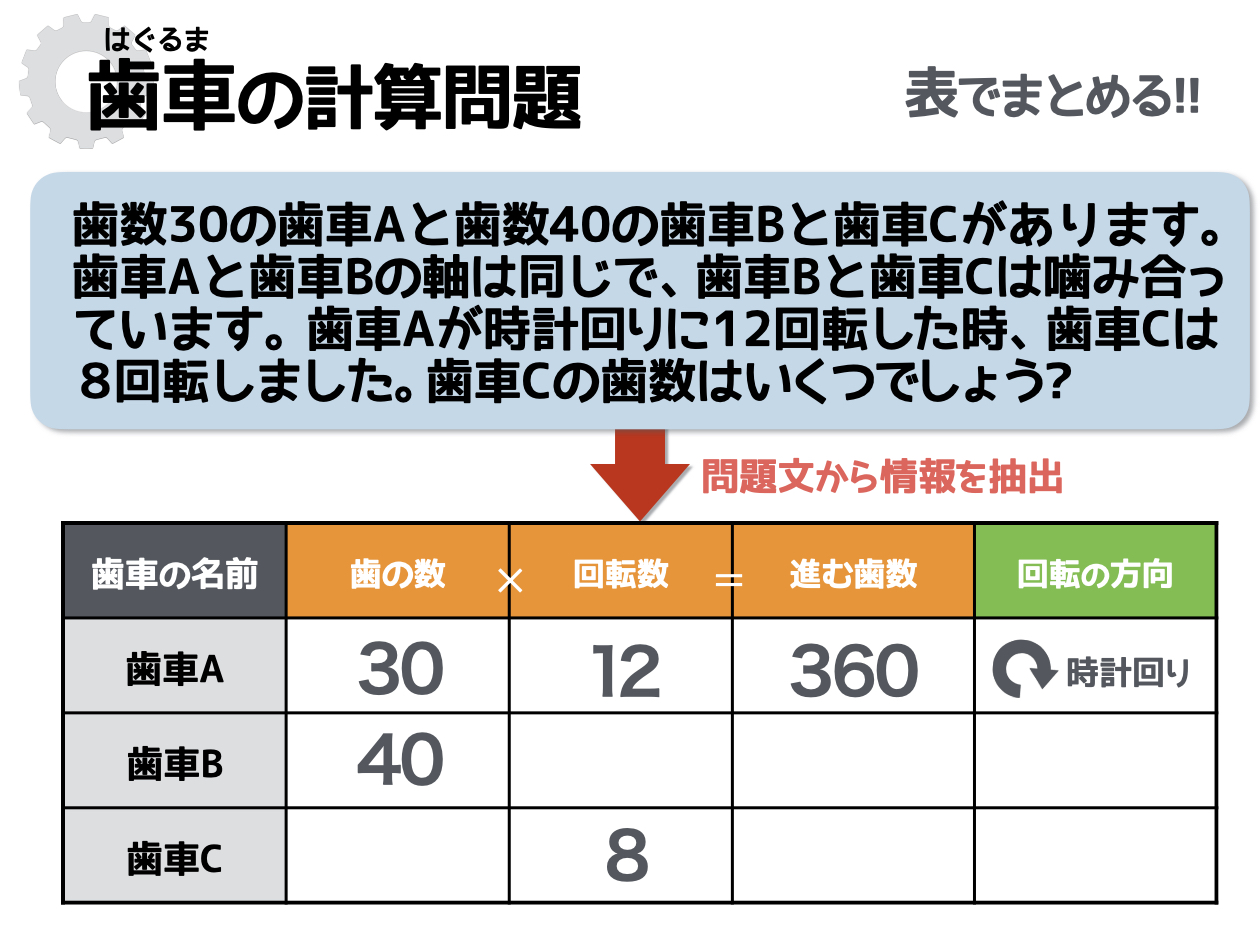
表を埋められたら、次のステップに移りましょう。大切なポイントを改めておさらいしておきます。
■噛み合った歯車(歯車Bと歯車C)
進む歯数は同じ、回転の方向は逆
■軸が同じ歯車(歯車Aと歯車B)
回転数は同じ、回転の方向も同じ
これらの関係性をもとに、表の空欄を落ち着いて埋めてみてください。ゴールまでは、あと少しです!
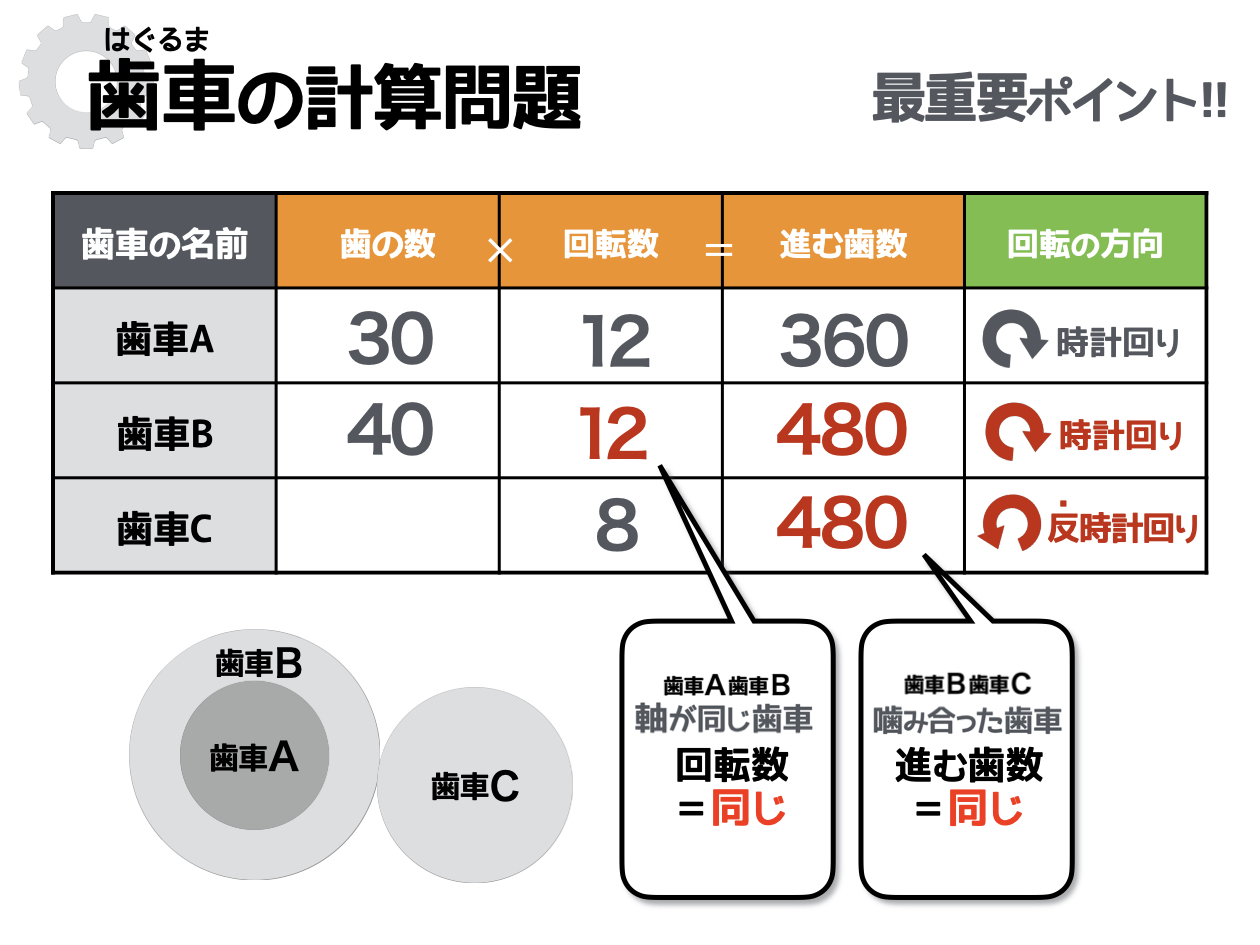
※図の縮尺は目安です
最後に、残りの空欄を計算で埋めていきましょう。答えは、表のなかに見えてきましたか? 例題で求められているのは歯車Cの歯数なので、答えは「60」ですね。
まとめ
「表を使った解法」を自分のモノにできれば、応用問題にも対応できます。回転の方向を求められても、歯の数を求められても、回転数を求められても、考え方は同じ。落ち着いて情報を整理することで、攻略は可能です。
ちなみに比や逆比を使って一気に解くこともできますが、こうした解法をいきなり理解するのは難しいものです。一方で多少遠回りに思えても、まずは基礎に立ちかえり、基本的な情報を表にまとめて整理していくことで、答えがすんなりと導き出せることは少なくありません。歯車の問題で悩んでいる場合には、お伝えしたポイントを踏まえつつ、表を使った解法にもぜひチャレンジしてみてくださいね。
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

