
樹形図の書き方のコツと注意点 中学受験で「場合の数」をマスターする!
「場合の数」の問題は、「順列」と「組み合わせ」の2つのパターンがあります。なかでも「組み合わせ」は、あることに対する、起こり得るパターンを全て数えなくてはいけないため、頭を抱えてしまう子供も多いのではないでしょうか。
中学受験では計算ではなく、書き出して数えることで答えを出す問題がほとんどです。そして、数え間違えを防ぎつつ、効率的よく書き出す方法が「樹形図」です。
今回はどんな場合に樹形図を使うのか、書くコツや注意点について解説します。
Contents [hide]
樹形図を使う「組み合わせ」の問題の見分け方
「場合の数」の「順列」は、並び順を気にするもの。「組み合わせ」は並び順を考えず、組み合わせのみを考えます。問題を見た時に、順列の問題か、組み合わせの問題か判断するポイントは問題文にあります。
順列の問題の見分け方
順列は並び順を気にするので、問題文に「順番」というキーワードが出てきたら順列の問題です。たとえば、
■例
リレーで、A、B、C、Dが走る順番は何通りあるのか
といった問題が挙げられます。
注意したいのが整数の組み合わせ。3桁の数字の組み合わせをつくる時に「0」など、先頭に来てはいけない数字があるものは順番が重要になります。ですので「◯ケタの整数は何種類か」という問題も順列です。
順列の問題の解き方
先ほどの、「リレーで、A、B、C、Dが走る順番は何通りあるのか」について、実際に解いてみましょう。
解く時に必要となるのが「樹形図」と呼ばれる方法です。まず第一走者を「A」とした場合に考えられるケースを樹形図で書き出してみます。
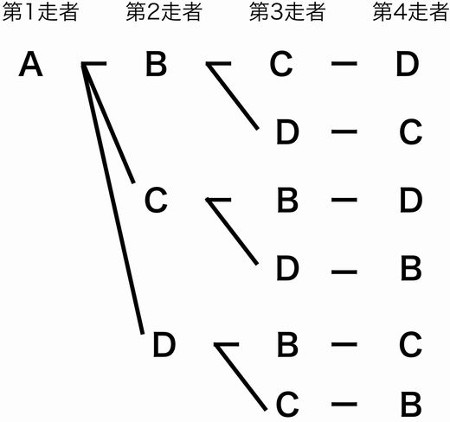
同じように、第一走者が「B、C、D」のときのケースも書いてみましょう。
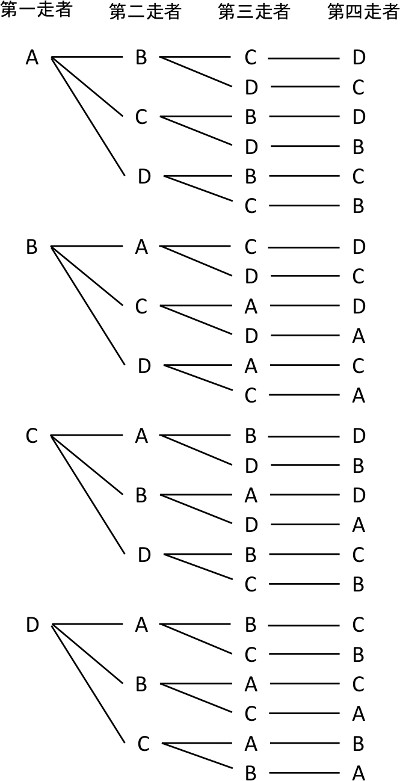
上記を数えてみると、答えが「24通り」あるとわかります。
樹形図を書いていると、B、C、DはAと同じパターンであると気づくと思います。その場合は、最初だけ樹形図で書き出せば、計算に入れるといった教え方が可能です。
第一走者Aの樹形図のみ書き、その場合は「6通り」であると導き出します。あとは、第一走者になる可能性がある人数をかけます。第一走者になる可能性があるのは「A、B、C、D」の4名なので、「4×6=24」で24通りという答えがでます。
最初から樹形図を使わずに計算で求めることもできますが、基礎を理解していないと後々つまずきやすいため、計算式だけを覚え込ませないよう注意しましょう。
組み合わせの問題の見分け方
組み合わせの問題は、順番は関係ないもの。人の選び方(グループ分け・チーム分け)が問題になることが多いです。たとえば、
■例
5人のうち◯人をグループにする場合、何通りの方法があるか
というものが、それにあたります。
この場合は順列のように計算で求めると、同じ組み合わせを数えてしまうため、樹形図で考える必要があります。
樹形図での数え間違いをなくす! 樹形図を書くコツとポイント2つ
「樹形図で考える問題とわかったら、さっそく樹形図を書いて問題を解きたい!」と、いきなり書き始めると数え間違いをしてしまう可能性も。樹形図を書くポイントは2つあります。
樹形図を書くときは「規律性」を考える
まず重要なポイントは「規律性」。A、B、C、D、Eと5つの項目がある場合は、アルファベット順に書く。問題文に「田中、鈴木、佐藤、山本、木下」という順で書かれている場合は、その順番で書くことが重要です。
規律性がない場合、重複して数えてしまったり、数え洩らすことがあります。そのため、アルファベット順、名前は出てきた順、など規律性をつくって樹形図を書くように練習しましょう。
樹形図を書くときは「名前をつける」
次に重要なのが「名前をつける」ことです。問題のなかには「5人の中から3人掃除当番を選ぶ」など、5人の名前が書かれていないことがあります。
その場合は自分で、A、B、C…など、自分でわかりやすい、簡単な名前をつけて樹形図を書くといいでしょう。
「5人の中から3人掃除当番を選ぶ」を樹形図にすると、以下のようになります。
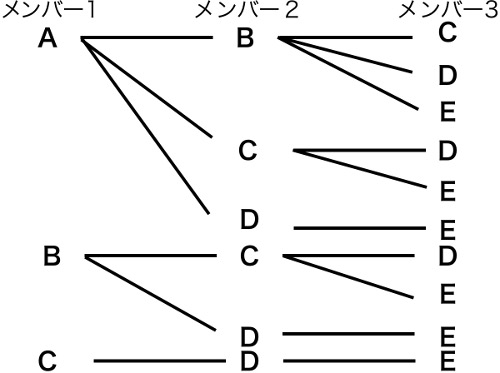
答えは「10通り」です。
樹形図を書く時の注意点! 樹形図を書かない方がおすすめの場合
樹形図を書くと、視覚的にも簡単に場合の数の問題を解くことができます。しかし、組み合わせの問題の場合、樹形図で全ての問題が解けるのかというと、残念ながらそうではありません。
樹形図を書かない方がおすすめのパターン
登場人物が多くて樹形図をたくさん書かないとといけない。そんなときは樹形図を書くことはおすすめしません。
少ない時間で多くの問題を解くには、スピードも大切です。100以上の樹形図を書いているとそれだけで試験時間が終わってしまいます。そのため、時間がかかりそうだと思った場合は、樹形図を書くのは一度やめてみることをおすすめします。
樹形図は規律性をつくる練習を
場合の数の問題、特に組み合わせは、樹形図を使って解くことがわかりましたね。
樹形図はほかの人が書いているのを見ると、簡単そうにみえますが、自分で書くとなかなか難しいもの。特に子供は、規律性を無視して樹形図を書いてしまったり、同じ物を重複して数えたりしがちです。
必ず自分で樹形図を書く練習をさせて、間違った場合にはなぜこの場合は書かないのか、この順番で書くのか、ということを一緒に書きながら教えてあげるといいですね。本番緊張している状態でも数え間違えることのないように普段から練習して備えましょう。
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

