３つのベン図でも慌てない！ ダブルカウントの理解であっさり解ける

中学入試でもよく出題される集合の問題。ベン図を使って解くのが一般的ですが、私の息子がぶつかってしまった壁があります。ベン図が３つになるとわからなくなってしまうのです。２つまでのベン図は理解できたのに……。

以下のような症状の場合は私の息子と同じ壁にぶつかっているかも知れません。その場合は、ぜひ本記事を参考にしてみてください！

なぜ３つになるとわからなくなるのか

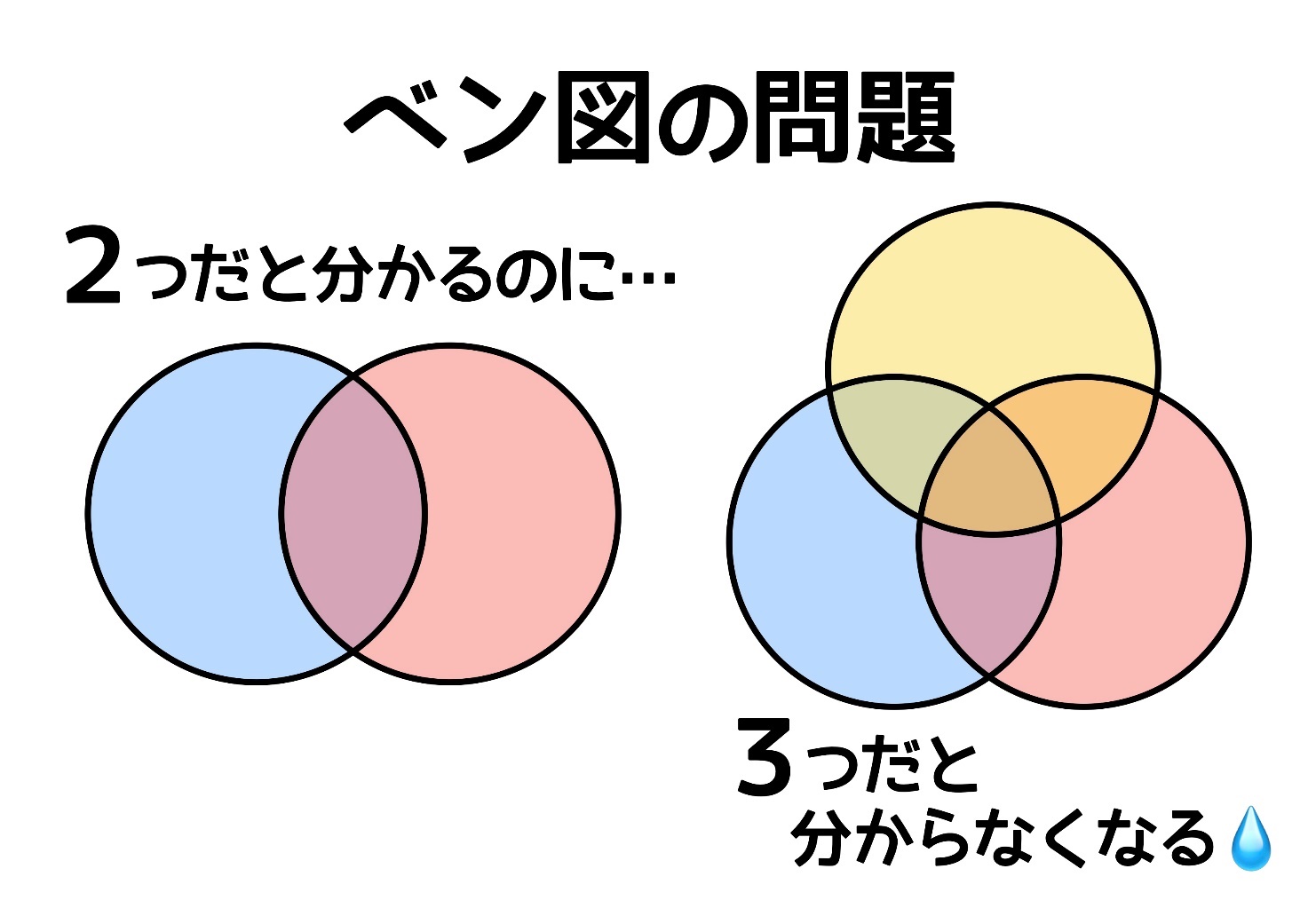
２つのベン図だと理解できるのに、３つになると途端にわからなくなってしまう。理由はどこにあるのでしょうか？ 息子とベン図の問題に取り組む中でわかってきた理由はシンプルでした。

３つになると頭のなかで想像できなくなる

２つのベン図の表は２×２の簡単な形式で書くことができますよね。書けといわれれば多くの小学生が書くことができるのではないでしょうか。では３つのベン図はどうでしょう？ 途端に書けなくなる小学生が多いのではないでしょうか？ それもそのはずです。

３つのベン図の表をまともに書こうとすると、もはや２次元の表では表現できず、２×２×２の３次元の表 になります。当然、頭のなかで想像することも難しくなるでしょう。

３つのベン図になると途端にわからなくなるのは、頭のなかで想像できる範囲を超えていることに起因します。

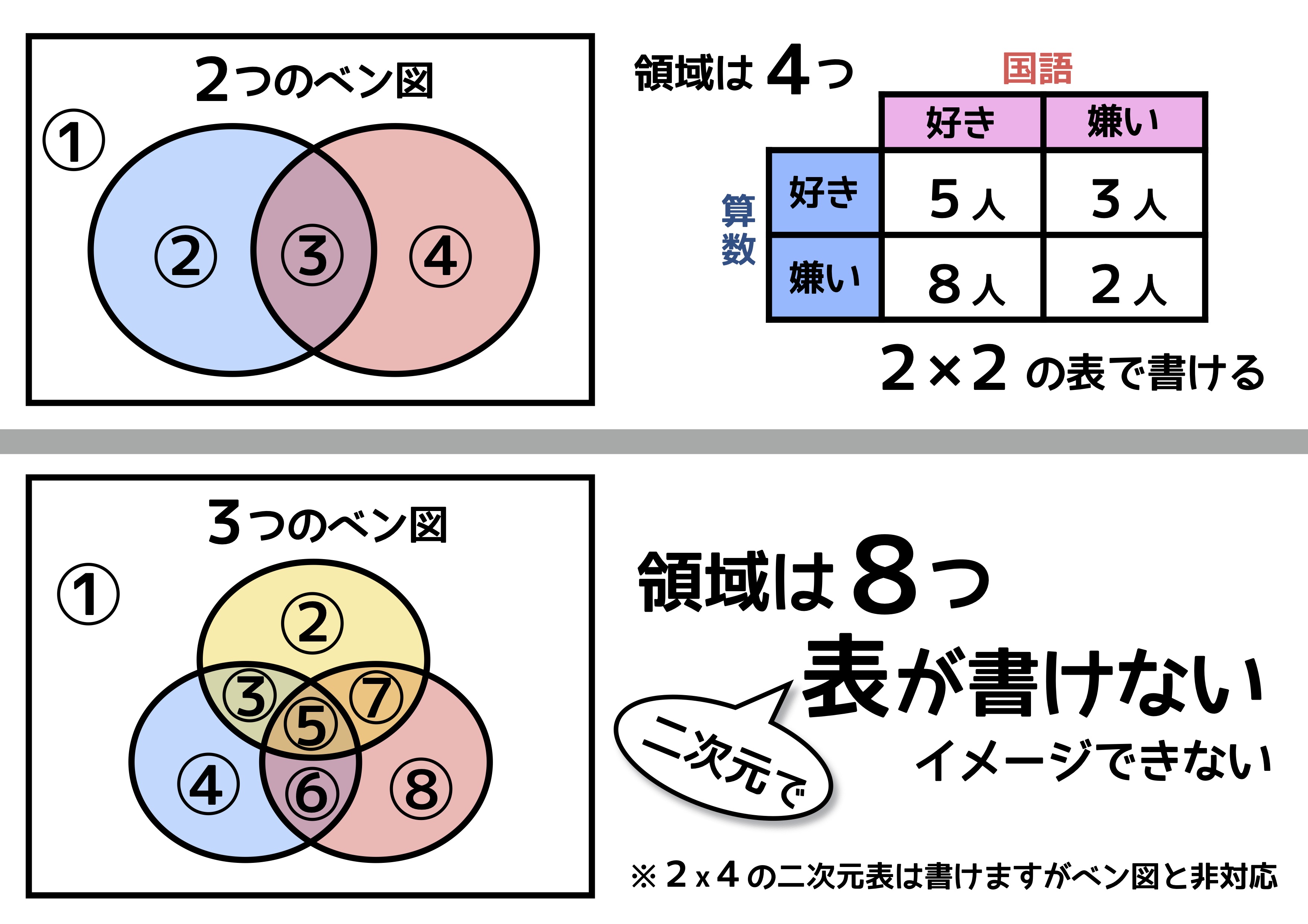
結果としてテクニックが必要

頭のなかで想像できる範囲なら自力で何とか解法を見つけ出すこともあるでしょうし、なんとなく答えにたどり着けることもあるでしょう。ところが想像すらできない問題は、解き方を知らなければ解けません。つまりテクニックを知っているか知らないかで得点できるかが決まります。

３つのベン図になると途端に問題が解けなくなってしまう子供は、２つのベン図の問題をなんとか解けてしまったが故に、３つのベン図のテクニックを知らないまま先に進んでしまっている可能性があります。私の息子は、まさにこの状態でした。

ダブルカウントを理解すればあっさり解ける

実はベン図の問題はダブルカウントというテクニックを知ってしまえば意外とあっさり解くことができます。しかも２つのベン図でも３つのベン図でも使える共通したテクニックです。

ダブルカウントとは何か

ダブルカウントとは、２つのベン図が重なった部分のことです。問題を見ながら、ダブルカウントの概要をお伝えしたいと思います。

ベン図を書くと次のようになります。そして２つのベン図が重なった赤い部分がダブルカウントの部分です。

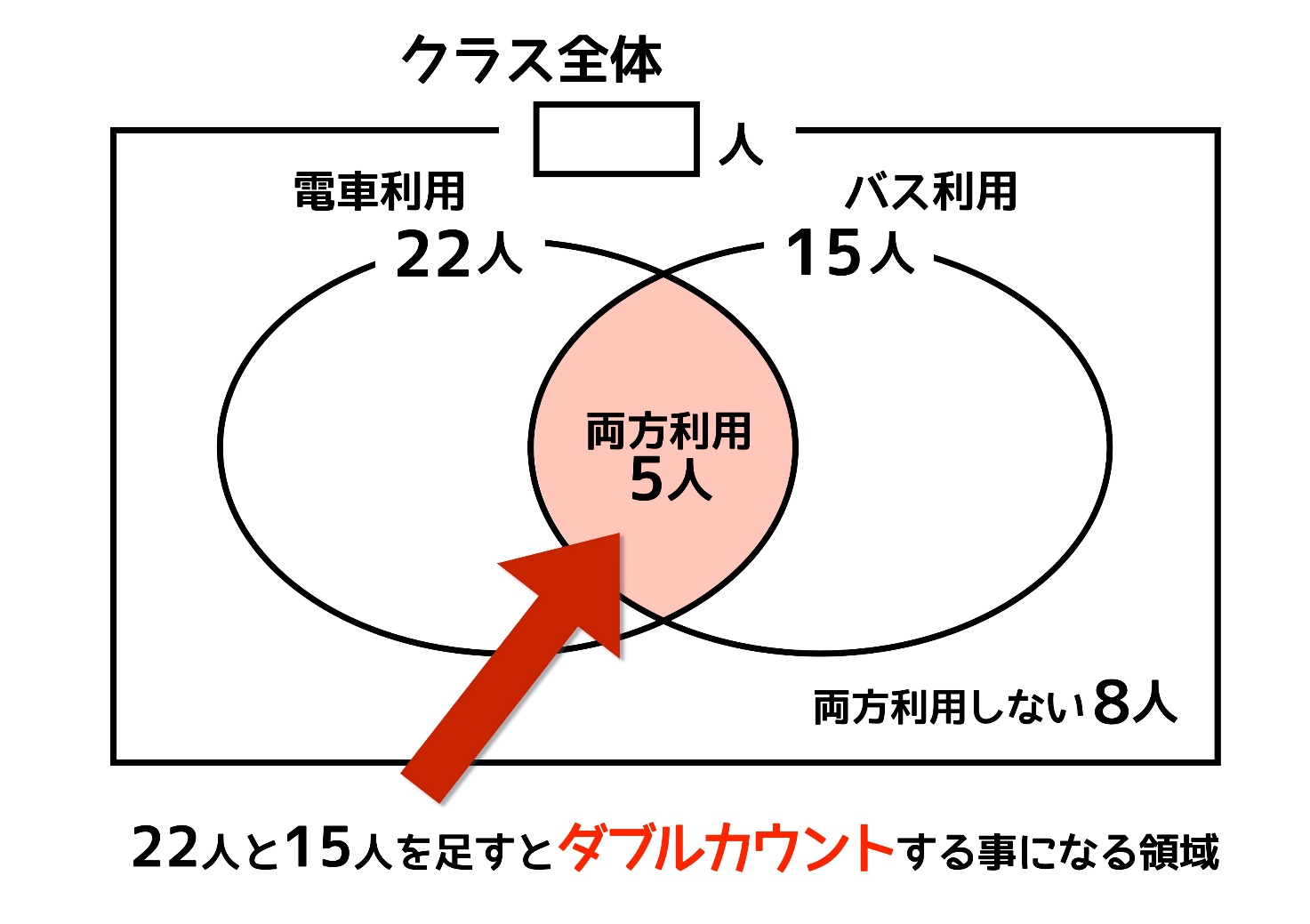
ダブルカウントした部分を後から引き算するという考え方が大切

クラス全体の人数はどのように求めればよいでしょうか？ ベン図に出てくる領域を全て足してあげればクラス全体の人数が計算できます。さっそく全ての領域の人数を足してみましょう。

子供もすぐに気づくかと思いますが、この式は間違っていますね。

ダブルカウントの部分の人数を２回足してしまっています。電車を使う生徒として１回、バスを使う生徒として１回、合計２回です。

ですので、２回足してしまった部分は忘れずに引き算をしてあげましょう。これでクラス全体の人数がわかりますね

ポイントは、２回足してしまった部分、つまりダブルカウントの部分を引き算するという考え方です。実は２つのベン図の場合は、このような考え方をしなくてもベン図を眺めながら何となく解けてしまいます。それでも足してからダブルカウント分を引くという考え方を覚えましょう！

３つのベン図の場合はトリプルカウントを駆使

３つのベン図の場合は、２つのベン図が重なっているダブルカウントの領域に加え、３つのベン図が重なっているトリプルカウントの領域もあります。どのように扱えばよいでしょうか？ とてもシンプルです。２回足してしまったら１回分を引き、３回足してしまったら２回分引けば良いのです。

３つのベン図の実践問題で試してみる

ベン図が３つともなると問題文にヒントとなる人数がワンサカ出てきます。２つのベン図は領域が全部で4つなのに対し、３つのベン図は領域が８つにもなるので当然ですね。落ち着いて問題文を読み解いていきましょう。

問題をよく読みそれぞれの領域に数を埋める

最初の作業は、慌てずに問題文をよく読み、ひとつずつヒントで与えられた数字をベン図に書き入れていく作業です。落ち着いて埋めましょう！

わからない領域は空欄の四角を置いておきましょう。またアンケートには最低１つを選ぶよう指示があるので、どれも選ばない生徒は0人ですね。

式を立てるときに、ダブルカウントとトリプルカウントの引き算を意識

それでは式を立ててみましょう。和食を選んだ人、洋食を選んだ人、中華を選んだ人を全て足してしまうと、ダブルカウントとトリプルカウントが発生しますね。ダブルカウントとトリプルカウントはベン図では以下の領域になります。

式を立てる時には、ダブルカウントした部分とトリプルカウントした部分を忘れずに引き算します。

あとは計算をすれば答えが見えてくる

和食と中華の2つを選んだ生徒が2人であることが分かりますね。そうすれば、ベン図の各領域が次々と埋まってきます。問題文で求められているのは、中華だけを選んだ生徒の人数ですから、答えは10人となります。

まとめ

３つのベン図になると途端にわからなく理由。それは２つのベン図が何となくできてしまうが故に、ベン図のダブルカウントやトリプルカウントのテクニックを知らない為である可能性があります。実際の問題を通してこのテクニックを知ればあっさり解けてしまいますので、落ち着いて練習することをおすすめします！

※記事の内容は執筆時点のものです