フィボナッチ数列とは？ 問題に隠れた規則性に気づけるようにしよう

中学入試では、並べられた数字から規則性を見つけ出す問題がよく出題されます。数列で有名なものといえば、等差数列、等比数列、階差数列などですが、ひときわ目立つ名前の数列があります。それがフィボナッチ数列です。名前からして異彩を放っていますが、その性質も神秘に満ちたもので、魅了されてしまった科学者も多くいるほどです。今回は中学受験に向けてフィボナッチ数列にどう対処すべきかを、例題を交えながら解説します。

フィボナッチ数列とは？

まずは、実際のフィボナッチ数列をみてみましょう。

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144……

はじめて見た子にとっては、まったく規則性のないデタラメな数列に見えてしまいますよね。しかしいったん理解してしまえば、とてもシンプルな規則で数字が並んでいることがわかります。どんな規則で数字が並んでいるのでしょうか？

まずは規則性を理解する

まずは規則性を理解しましょう。数列の規則性を見つけるための王道の手段は、各項の差に着目することです。ではさっそく各項の差を計算してみます。

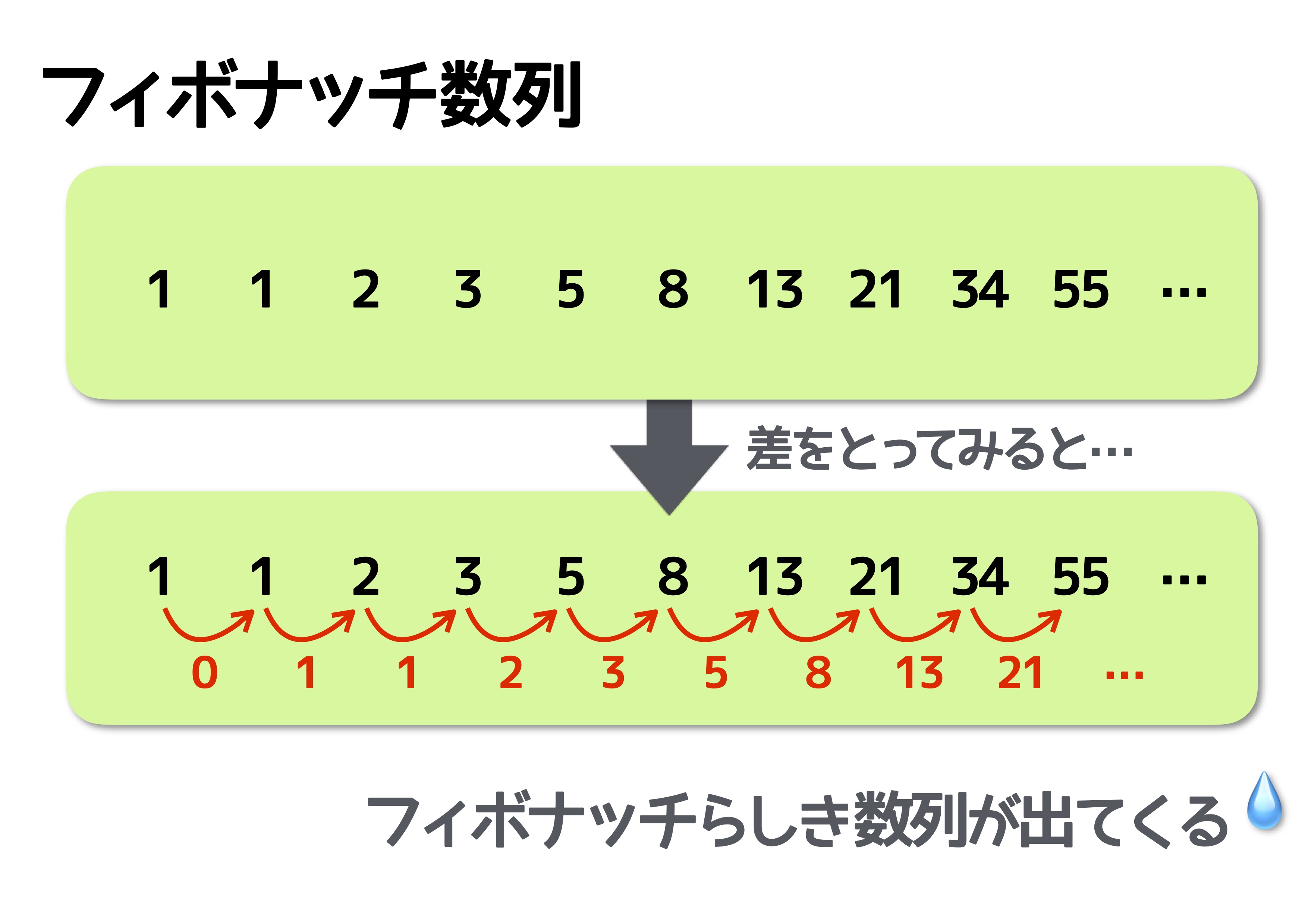
差を計算すると、フィボナッチ数列らしき数字が出てきました。フィボナッチ数列は、直前の2つの項の数を足したものが次の項の数になる数列です。そのためこのような結果になるんですね。規則自体はとてもシンプルです。一度でもフィボナッチ数列を見たことがあれば、規則性はすぐに理解できるでしょう。

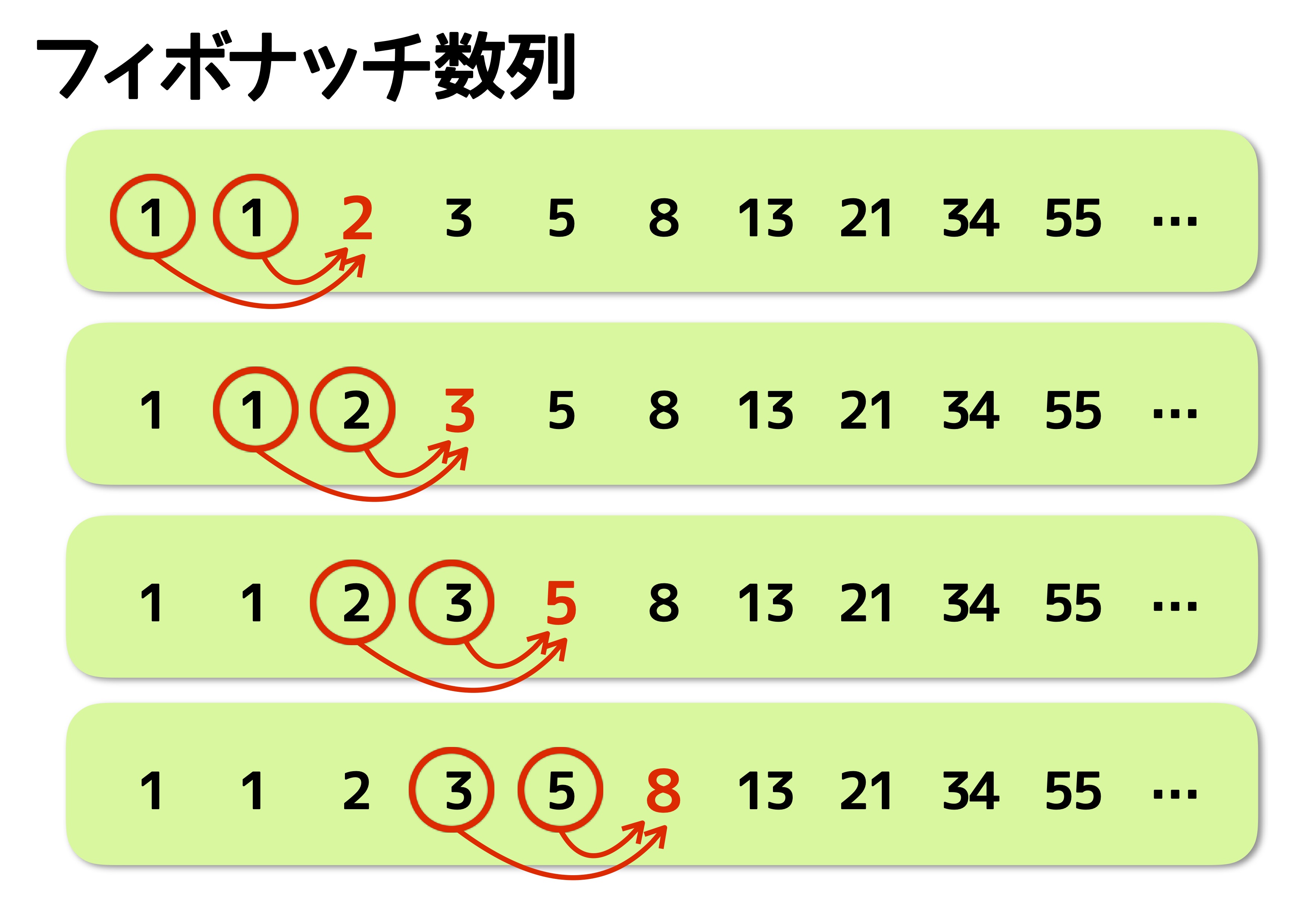
自分で書いてみると簡単さがわかる

フィボナッチ数列の問題に出くわしたときは、数列をテスト用紙に書くことがおすすめです。入試のときに慌てないで数列を書くためにも、実際にフィボナッチ数列を書いて、感覚をつかんでおきましょう。想像以上に計算しやすいので、書いてみると簡単さが実感できます。

余談ですが、フィボナッチ数列はなぜ“神秘的”といわれているのでしょうか？ その理由は、自然界のいたるところにフィボナッチ数列が存在するためです。ひまわりの種の並びや、オウム貝のデザイン、植物の花びらの数もフィボナッチ数列といわれています。

子供がもし興味をもつようであれば、身の回りに隠れたフィボナッチ数列をいっしょに調べてみると、フィボナッチ数列により興味が湧くかもしれません。

「場合の数の問題」にフィボナッチ数列が現れる

中学入試のフィボナッチ数列の問題は、「場合の数の問題」に絡めて出題されることが少なくありません。場合の数を求めているうちに、その規則性がフィボナッチ数列になっていることに気づかせる問題ですね。難しそうに聞こえますが、百聞は一見にしかず。「場合の数の問題」がフィボナッチ数列の知識をもとに解ける例をみてみましょう。

【例題1】 階段の登り方は何通り？

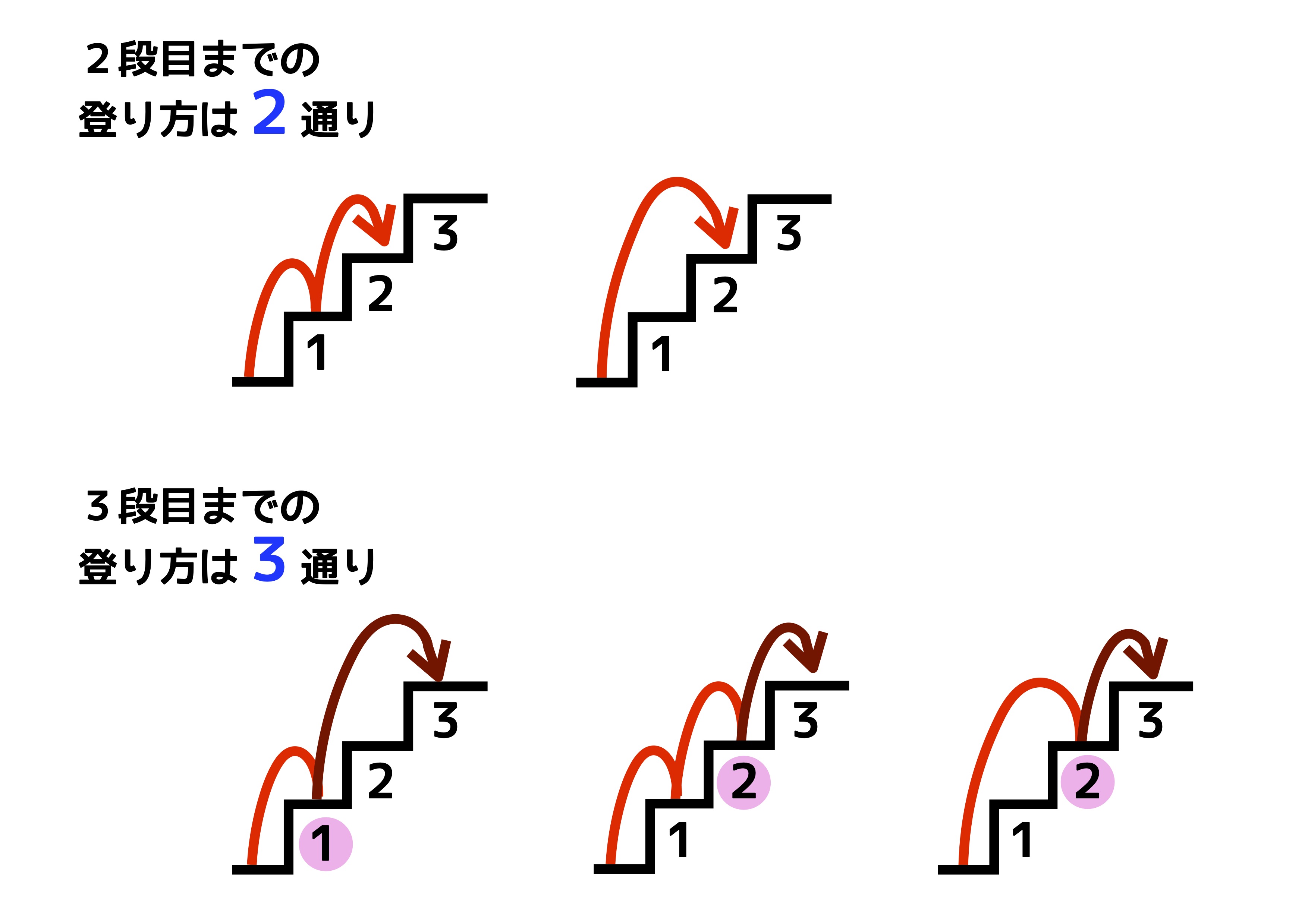
上の図のように、2段目までの登り方は2通りありますね。3段目までの登り方は、「1段目まで登ってから一気に3段目に到達する1通り」と「2段目まで登ってから3段目に到達する2通り」、合わせて3通りあることが分かります。それでは4段目までの登り方は何通りあるでしょうか？

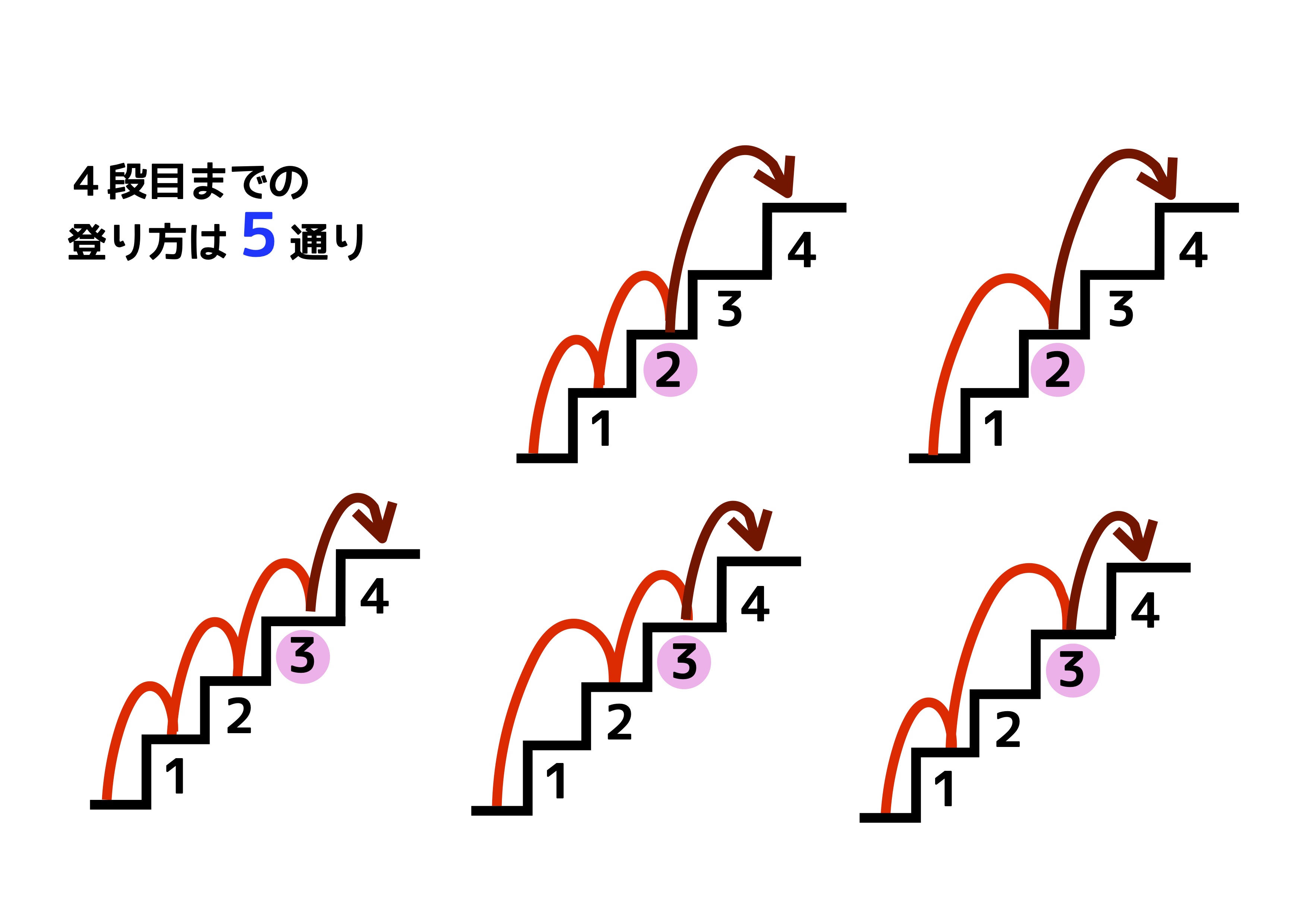
4段目までの登り方は、「2段目まで登ってから4段目に到達する2通り」と「3段目まで登ってから4段目に到達する3通り」があるので、合計5通りです。つまり、4段目までの登り方の「場合の数（5通り）」は、2段目までの登り方の「場合の数（2通り）」と、3段目までの登り方の「場合の数（3通り）」の合計になるのです。まさにフィボナッチ数列のような関係になっています。

階段の登り方の「場合の数」がフィボナッチ数列になっていることがわかれば、わざわざ図を書いて場合の数を考えなくても、答えを求めることができるようになります。では、6段目までの登り方は何通りあるでしょうか？ 数列を並べていけば、13通りであることがわかりますね。

6段目までの登り方であれば、図を描いて場合分けをしていけば力わざで解けてしまう場合もあります。しかし、15段目までの登り方を答えさせる問題があったらどうでしょうか？ 答えは、なんと987通り！ フィボナッチ数列であることに気づいていないと、とうてい解くことはできませんね。

【例題2】 タイルの並べ方は何通り？

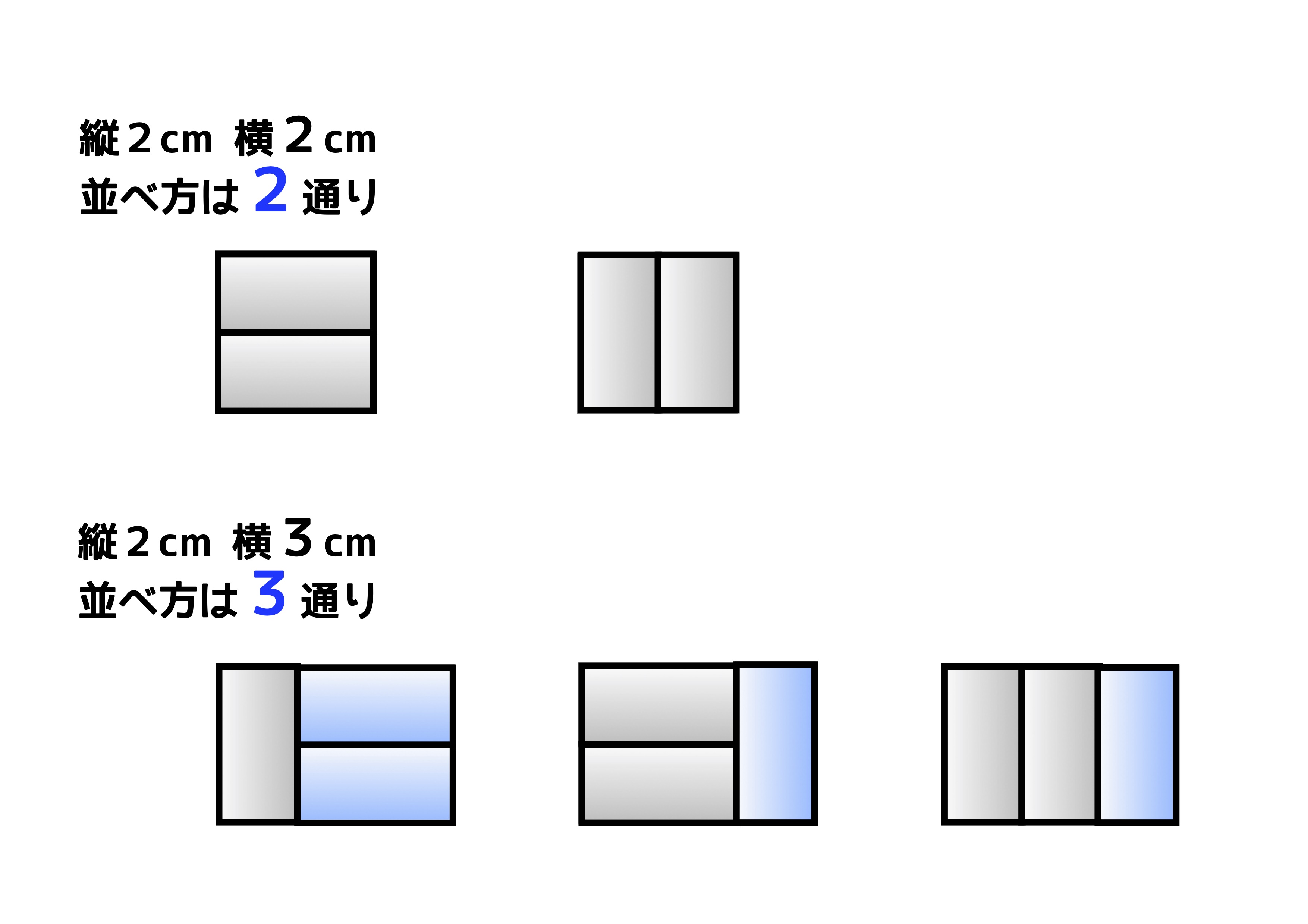
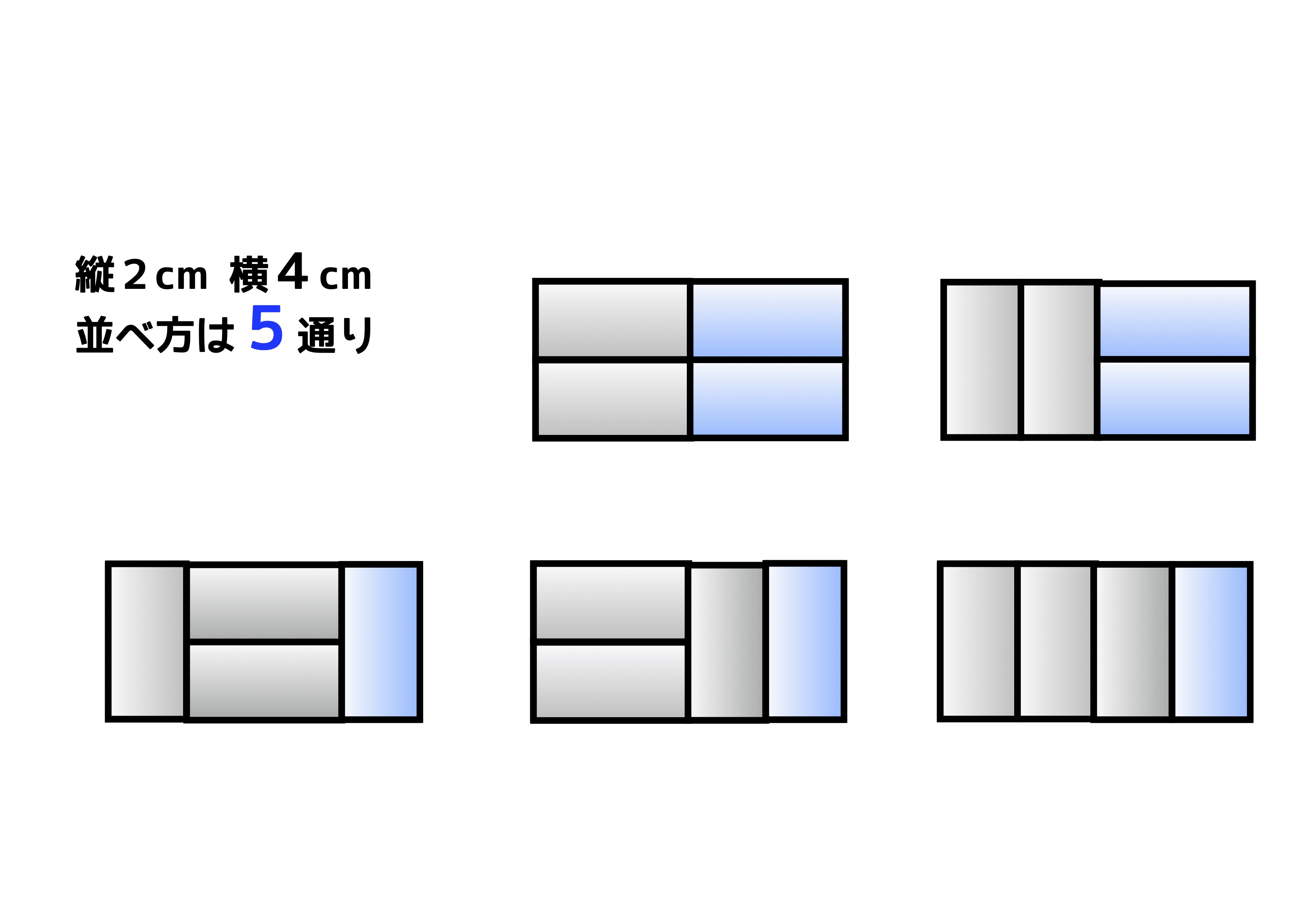
上の図のように、「縦2cm×横2cm」のタイルの並べ方は2通りあります。「縦2cm×横3cm」のタイルの並べ方は3通りです。それでは「縦2cm×横4cm」のタイルの並べ方は何通りでしょうか？ 正解は、5通りです。

このとき、「縦2cm×横4cm」の並べ方の「5通り」は、「縦2cm×横2cm」に並べた場合の「2通り」と、「縦2cm×横3cm」に並べた場合の「3通り」を合計したものと同じです。またしても、フィボナッチ数列が見えてきました。

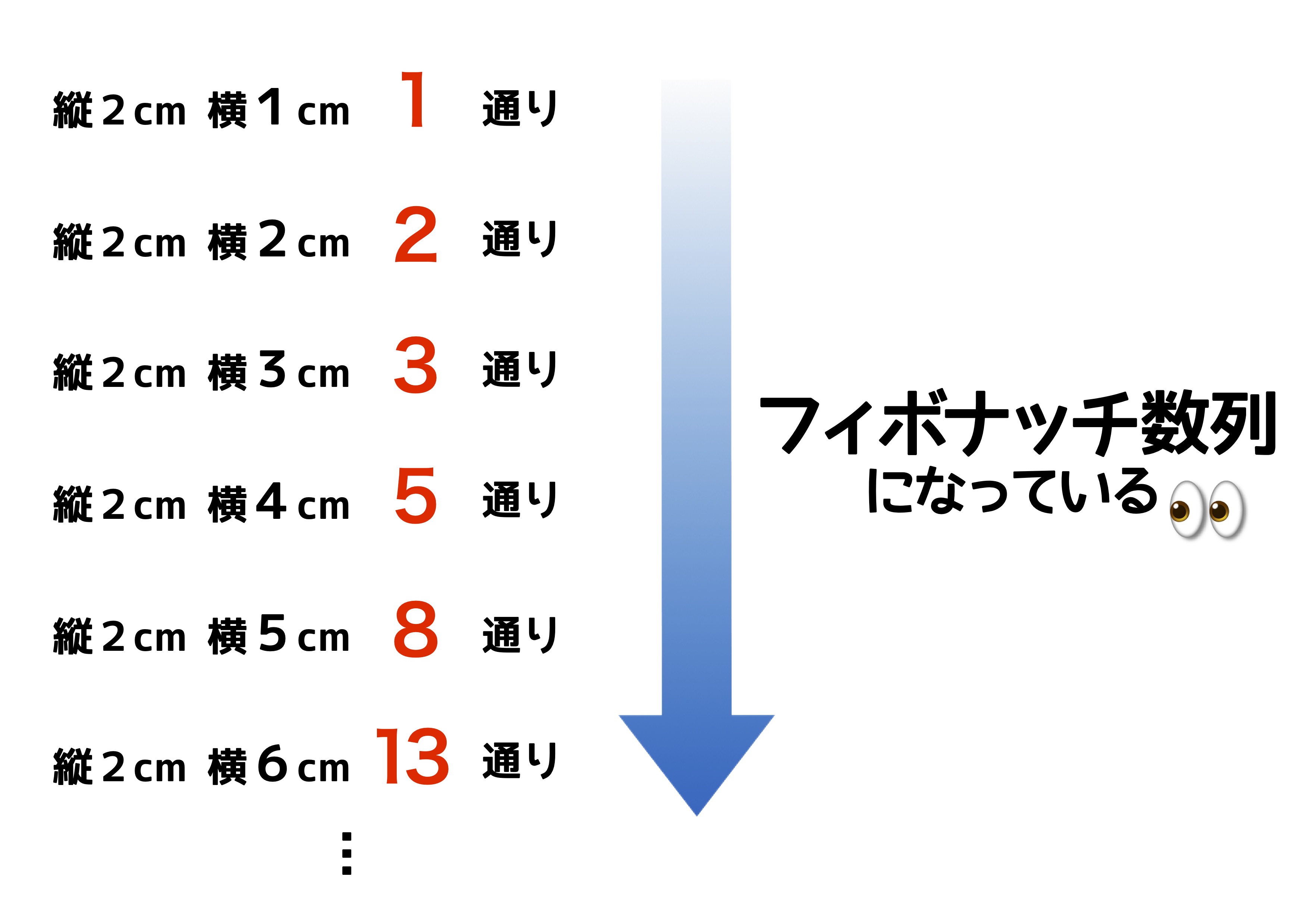
フィボナッチ数列だとわかれば、横の長さが何cmの四角形であっても、タイルの並べ方の「場合の数」が計算でわかります。問題文で問われている「縦2cm×横10cm」の四角形であれば、フィボナッチ数列を計算していくと89通りであることがわかりますね。

まとめ

自然科学の世界で、“神秘的で美しい”とされているフィボナッチ数列。中学受験でもよく出される題材です。「場合の数の問題」に隠れたフィボナッチ数列を紹介しましたが、紹介した2つの例題以外にも、「場合の数」がフィボナッチ数列の知識で解ける問題は中学入試では頻出です。「場合の数」を求めながらも、フィボナッチ数列の規則性が見いだせないか疑うクセがつけられるとよいですね。

※記事の内容は執筆時点のものです